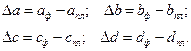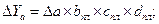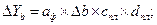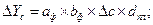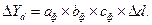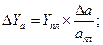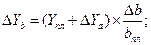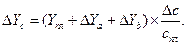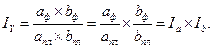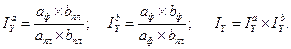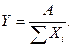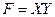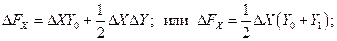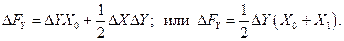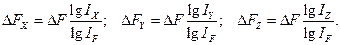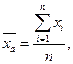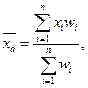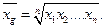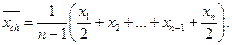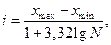Логарифмический метод
Обозначим индексами 1 и 0 данные, относящиеся к отчетному и базовому периодам соответственно.
В соответствии с рассматриваемой моделью можно записать:
Отметим, что логарифм здесь может быть любым — натуральным, десятичным или по любому другому основанию. Домножим обе части на ?z и разделим на lnz1z0. Получим:
Итак, прирост результативного показателя распределяется между факторами пропорционально логарифмам их изменения. Особенность метода в том, что при его использовании не требуется установления очередности действия факторов. Недостаток же заключается в том, что действует этот метод только для кратных и мультипликативных моделей. Пример 2.4 иллюстрирует использование логарифмического метода для анализа влияния факторов на изменение результативного показателя. Пример 2.4.
Анализ показывает, что направленность действий факторов противоположная, поэтому влияние каждого из них на изменение результативного фактора отчасти взаимно компенсируется. Задача 3 детерминированного факторного анализа представляет собой оценку влияния относительного изменения факторов на относительное изменение результативного показателя, т.е. определение отношения величины прироста, вызванного изменением любого фактора, к величине результативного показателя за базисный период в процентах. Она решается с помощью индексного метода и будет рассмотрена в разделе 2.7.4. Заканчивая раздел, отметим, что детерминистский подход достаточно распространен в анализе финансово-хозяйственной деятельности предприятий, поскольку позволяет выявить множество связей между факторами, влияющими на деятельность предприятия. Вместе с тем принципиальным недостатком детерминированного подхода является то, что он не позволяет разделить результаты влияния одновременно действующих факторов, которые не поддаются объединению в одной модели. Смысл данного утверждения совершенно очевиден. Дело в том, что любое предприятие работает в условиях действия множества факторов; объединить эти факторы в какую-либо модель, тем более жестко детерминированную, ни теоретически, ни практически не представляется возможным. Поэтому любое факторное разложение является весьма и весьма условным. Для примера приведем две модели, достаточно широко распространенные в факторном анализе:
где Т — товарооборот (выручка от реализации); Ч — численность работников; В — выработка на одного работника; Ф — фондоотдача; ОС — величина основных средств. Предположим, что проводится факторный анализ динамики изменения товарооборота с использованием этих двух моделей. Для этого необходимо построить следующие факторные разложения:
Из самой сути факторного анализа понятно, что общее приращение товарооборота в обеих моделях одно и то же, т.е.
Источник
Вопрос 12. Интегральный и логарифмический методы детерминированного факторного анализа
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях. Наиболее эффективен в случаях, когда исходные данные содержат уже определенные ранее относительные приросты факторных показателей в процентах или в коэффициентах.
Способ абсолютных разниц используется только в мультипликативных и мультипликативно-аддитивных моделях:. При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, располеженных слева от него в модели.
Для мультипликативной модели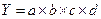 
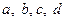
, изменение результативного показателя под влиянием факторов 
будет рассчитано следующим образом. Вначале определяются абсолютные отклонения по каждому факторному показателю:
Далее определяется изменение величины результативного показателя под влиянием каждого фактора:
Для модели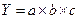 
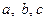
, изменение результативного показателя под влиянием факторов 
будет рассчитано следующим образом:
Согласно этому правилу, для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в виде десятичной дроби.
Чтобы рассчитать влияние второго фактора, нужно к плановой (базисной) величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора.
Влияние третьего фактора определяется аналогично: к плановой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.
Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов значительно сокращается количество вычислений.
Индексный методоснован на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту).
С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.
Имеем кратную модель вида: 
Чтобы установить, как изменился результативный показатель за счет факторов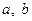 
нужно рассчитать агрегатные индексы:
Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты продукции в целом и за счет каждого фактора в отдельности.
Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязано и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов цепной подстановки, абсолютных и относительных разниц присоединяется к одному из факторов, как правило, к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в модели. В результате этого величина влияния одного фактора преувеличивается, а другого – приуменьшается.
Чтобы избавиться от этого недостатка, в детерминированном факторном анализе используется интегральный метод, который применяется для измерения влияния факторов в мультипликативных, кратных и смешанных моделях кратно-аддитивного вида
Использование этого способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц и избежать неоднозначной оценки влияния факторов. Потому, что в данном случае результаты не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается полностью.
Для двухфакторной мультипликативной модели типа 
Для расчетов влияния факторов с помощью трехфакторных (и более) мультипликативных моделей, кратных и смешанных моделей, используют специально разработанные готовые алгоритмы расчетов.
Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы подставить необходимые числовые данные и сделать не очень сложные расчеты с помощью калькулятора в Excel. При этом достигается более высокая точность расчетов.
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. При использовании данного способа, как и при интегрировании, результат расчета не зависит от местоположения факторов в модели и по сравнению с интегральным методом обеспечивается еще более высокая точность расчетов.
Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого факторов на уровень результативного показателя. В этом его преимущество, а недостаток – в ограниченности сферы применения.
В отличие от интегрального метода (подобно индексному) при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения).
Для модели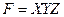 
влияние факторов определяется следующим образом:
При выполнении расчетов с помощью данного метода не имеет значение вид логарифма (натуральный или десятичный).
Вопрос 13. Традиционные методы экономической статистики (метод средних величин, метод группировок)
Помимо специальных методов анализа аналитики в своей работе успешно используют методы, разработанные в рамках экономической статистики и других наук. Их широкая распространенность, простота и историчность дают основание условно называть их традиционными.
В любой совокупности экономических явлений, процессов, объектов наблюдаются различия между отдельными ее единицами. Одновременно с этими различиями существует нечто общее, что объединяет совокупность и позволяет нам отнести все рассматриваемые объекты и явления к одному классу (каждому студенту известно, что такое средний балл на экзамене, для характеристики климата, используется показатель средней температуры воздуха и т.д.)
Средняя величина – обобщающий показатель, характеризующий типичный уровень варьирующего признака на единицу совокупности в определенных условиях места и времени.
Таким образом, роль средних величин заключается в обобщении, т.е. замене множества индивидуальных значений признака некоторой средней величиной, характеризующей всю совокупность явлений. Не только средние значения величин, но и тенденции их изменения можно рассматривать в качестве индикаторов положения предприятия на рынке и успешности его финансово-хозяйственной деятельности.
Существую несколько видов средних величин. Наибольшее распространение в микроэкономическом анализе получили: средняя арифметическая, средняя геометрическая и средняя хронологическая.
Средняя арифметическая – среднее слагаемое. При ее вычислении общий объем признака распределяется поровну между всеми единицами совокупности (например, средняя заработная плата), определяется по формуле
где: п – число единиц в совокупности;
хi – индивидуальное значение i-го признака.
Если же объем совокупности велик и представляет собой ряд распределения, то используют значение средней арифметической взвешенной (например, расчет среднего балла по группе):
где: wi – частота проявления признака со значением xi.
Средняя геометрическая – используется для расчетов средних темпов роста (объемов производства, инфляции и т.д.).
Средняя хронологическая – используется для усреднения моментных показателей (т.е. на определенную дату). Этот вид средней используется для расчета средних товарных запасов, средней дебиторской задолженности, средней численности работников и др.
Группировка – расчленение совокупности данных на группы с целью изучения ее структуры или взаимосвязей между компонентами. Например, группировка хозяйствующих субъектов по формам собственности населения по уровню доходов, изучение состава населения по полу, возрасту и т.д.
Важнейшим вопросом при проведении такого рода исследования – выбор интервала группировки. Существуют два основных подходов к его решению.
1. Деление совокупности данных на группы с равными интервалами значений. Для определения длины интервала используют формулу Стерджеса:
где: хmax – максимальное значение признака в изучаемой совокупности;
xmin – минимальное значение признака в изучаемой совокупности;
N – число наблюдений в совокупности.
2. Деление совокупности данных на группы с неравными интервалами значений (возрастающими или убывающими). Этот подход обычно применяется при большой вариации и неравномерности распределения признака по всему интервалу.
При выборе размера интервала группировки руководствуются здравым смыслом и логикой, опираясь при этом на распределения прошлых периодов и традиционно сложившиеся подходы в группировке. При этом следят за равнозаполняемостью интервалов.
В анализе используются в основном два вида группировок.
Структурные группировки предназначены для изучения структуры и состава совокупности, и происходящих в них сдвигов (изучение состава населения по полу, возрасту и другим признака).
Аналитические группировки предназначены для изучения взаимосвязей между двумя и более показателями, характеризующими исследуемую совокупность (группировка предприятий определенной отрасли экономики по уровню производительности труда для выявления ее влияния на себестоимость).
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
