- ДЕТАЛЬНАЯ РАЗБИВКА КРУГОВЫХ КРИВЫХ
- Разбивка кривых на местности.
- Оставьте свой комментарий
- Оставить комментарий от имени гостя
- Комментарии
- Закрепленные
- Понравившиеся
- Последние материалы
- Заключение (Грунты)
- Представления о решении задач нелинейной механики грунтов
- Прочность грунтов при сложном напряженном состоянии
- Основные закономерности татического деформирования грунтов
- Упругопластическое деформирование среды и поверхности нагружения
- Описание схем и результатов испытаний грунтов с использованием инвариантов напряженного и деформированного состояний
- Инварианты напряженного и деформированного состояний грунтовой среды
- О коэффициентах устойчивости и сопоставление с результатами опытов
- Давление грунта на сооружения
- Несущая способность оснований
- Процесс отрыва сооружений от оснований
- Решения плоской и пространственной задач консолидации и их приложения
- Детальная разбивка кривых
- Способ прямоугольных координат
- Способ продолженных хорд
ДЕТАЛЬНАЯ РАЗБИВКА КРУГОВЫХ КРИВЫХ
Детальная разбивка кривой предусматривает не только закреп-ление на местности начала НК, конца КК и середины СК кривой, но и обозначение всей кривой, например, колышками через определен-ный интервал. Существует ряд способов разбивки круговых кривых: способ прямоугольных координат, способ углов, способ продолжен-ных хорд.
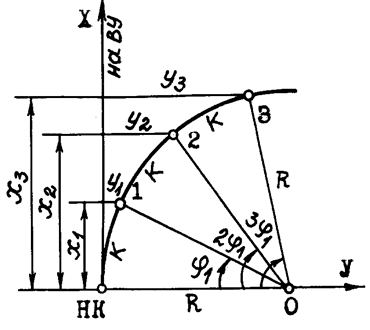
Способ прямоугольных координат (ординат от тангенса).
|
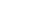
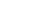


|
|
|
|
|
|
В эти формулы подставляют значение угла j1, зависящее от величины интервала К, которое можно найти из выражения:
j1= 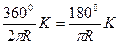
На местности откладывают от начала кривой НК по направ-лению на вершину угла поворота ВУ (по направлению тангенса) абсциссы Хi , а по перпендикулярному направлению ординаты Уi и закрепляют точки 1, 2, 3 и т.д. Так производят разбивку до середины кривой. Другую половину кривой разбивают с ее конца. Для определения координат Х и У существуют специальные таблицы.
Этот способ применяется на ровной площадке и является наиболее точным, так как точки 1, 2, 3 и т.д. выносят независимо друг от друга, поэтому ошибка положения одной точки не окажет влияния на положение других точек, чего нельзя сказать о рассмат-риваемых далее способах углов и продолженных хорд .
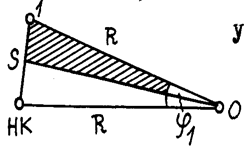
Способ углов (полярный способ).
|
|
|
|
|
Этот способ удобно применять в стесненных условиях, когда есть видимость между НК и точками 1, 2, 3. (например, на высокой насыпи, где способ прямоугольных координат неприемлем).
|
|

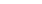
|
|
|
|
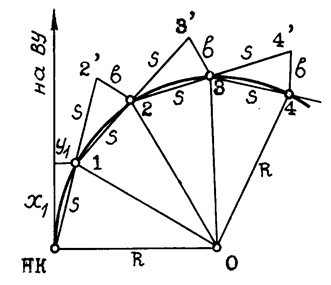
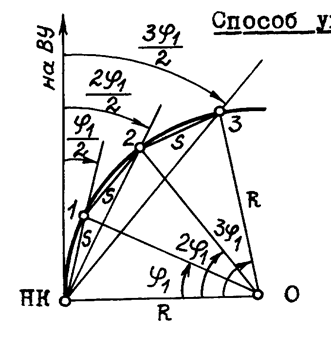
Способ продолженных хорд
|
Вначале по координатам Х1 и У1 выносят точку 1. Затем в створе НК-1 на расстоянии S от точки 1 отмечают вспомогательную точку 2’, от которой откладывают так называемое промежуточное
|
|
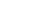




|
|
Этим способом одну половину кривой разбивают с HK, а дру-гую половину — с конца кривой КК. Способ применим в любыхстес-ненных условиях, в том числе и в выемке, где первые два способа неприемлемы.
Недостатком способов углов и продолженных хорд является снижение точности разбивки кривой по мере возрастания ее длины, так как положение каждой последующей точки определяется относительно предыдущей.
Источник
Разбивка кривых на местности.
Середину кривой СК закрепляют, отложив от ВУ по направлению биссектрисы отрезок, равный Б (или Бс).
На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.
Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.
Детальная разбивка кривых. При детальной разбивке кривую закрепляют на местности через 10 или 20 м, применяя разные способы.
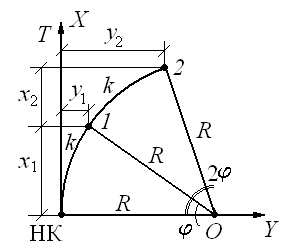
Способ ординат от касательной для круговой кривой. Для каждой точки i (рис. 15.7, а), задавая расстояние k от начала кривой, вычисляют ее координаты:
Здесь угол j выражен в радианах и равен j = k/R.
Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.
Рис. 15.7 Детальная разбивка кривых:
а – способом ординат от касательной для круговой кривой;
б – то же, для переходной и следующей за ней круговой кривой;
в – разбивка кривой электронным тахеометром
Способ ординат от касательной для переходной и следующей за ней круговой кривой (рис. 15.7, б). Для точек, расположенных в пределах переходной кривой, то есть при k £ l, координаты x, y вычисляют по формулам (15.8) и (15.9), принимая s = k. Для точек i, расположенных на круговой кривой, где k > l, вычисления выполняют по формулам:
Действия при разбивке кривой на местности аналогичны тем, что выполняют при разбивке круговой кривой.
Разбивка кривой с помощью электронного тахеометра. Выбирают на местности такую точку T (рис. 15.7, в), где обеспечена видимость точек будущей кривой и ее начала НК. В точке НК измеряют угол g и расстояние d. Вычисляют координаты точки Т:
По приведенным выше формулам вычисляют координаты точек кривой xi, yi (i = 1, 2, …).
Электронный тахеометр устанавливают в точке Т. Зная координаты точек Т, НК и i, вычисляют разбивочные элементы — углы bi и расстояния di. Построив тахеометром вычисленные углы и расстояния, находят и закрепляют положение точек кривой на местности.
Оставьте свой комментарий
Оставить комментарий от имени гостя
Комментарии
Закрепленные
Понравившиеся
Последние материалы
Заключение (Грунты)
При построении курса учитывалась необходимость его использования для различных гидротехнических специальностей и специализаций. В качестве основной части для студентов всех гидротехнических специальностей следует считать обязательным прочтение гл. 1—7. В гл. 8.
Представления о решении задач нелинейной механики грунтов
На современном этапе развития нелинейного направления механики грунтов оформились два основных подхода к решению практических задач расчета грунтовых оснований и сооружений: нелинейно-упругий и упругопластический (А. К. Бугров, С. С. Вялов.
Прочность грунтов при сложном напряженном состоянии
Для сред и материалов, обладающих сплошностью, предложено много различных условий прочности. Для оценки прочности грунтов наиболее широкое распространение получило условие Мора—Кулона (2.38), не содержащее промежуточного главного напряжения а2 и тем.
Основные закономерности татического деформирования грунтов
За последние 15. 20 лет в результате многочисленных экспериментальных исследований с применением рассмотренных выше схем испытаний получены обширные данные о поведении грунтов при сложном напряженном состоянии. Поскольку в настоящее время в…
Упругопластическое деформирование среды и поверхности нагружения
Деформации упругопластических материалов, в том числе и грунтов, состоят из упругих (обратимых) и остаточных (пластических). Для составления наиболее общих представлений о поведении грунтов при произвольном нагружении необходимо изучить отдельно закономерности…
Описание схем и результатов испытаний грунтов с использованием инвариантов напряженного и деформированного состояний
При исследовании грунтов, как и конструкционных материалов, в теории пластичности принято различать нагружение и разгрузку. Нагружением называют процесс, при котором происходит нарастание пластических (остаточных) деформаций, а процесс, сопровождающийся изменением (уменьшением)…
Инварианты напряженного и деформированного состояний грунтовой среды
Применение инвариантов напряженного и деформированного состояний в механике грунтов началось с появления и развития исследований грунтов в приборах, позволяющих осуществлять двух- и трехосное деформирование образцов в условиях сложного напряженного состояния…
О коэффициентах устойчивости и сопоставление с результатами опытов
Так как во всех рассмотренных в этой главе задачах грунт считается находящимся в предельном напряженном состоянии, то все результаты расчетов соответствуют случаю, когда коэффициент запаса устойчивости к3 = 1. Для…
Давление грунта на сооружения
Особенно эффективны методы теории предельного равновесия в задачах определения давления грунта на сооружения, в частности подпорные стенки. При этом обычно принимается заданной нагрузка на поверхности грунта, например, нормальное давление р(х), и…
Несущая способность оснований
Наиболее типичной задачей о предельном равновесии грунтовой среды является определение несущей способности основания под действием нормальной или наклонной нагрузок. Например, в случае вертикальных нагрузок на основании задача сводится к тому…
Процесс отрыва сооружений от оснований
Задача оценки условий отрыва и определения требуемого для этого усилия возникает при подъеме судов, расчете держащей силы «мертвых» якорей, снятии с грунта морских гравитационных буровых опор при их перестановке, а…
Решения плоской и пространственной задач консолидации и их приложения
Решений плоской и тем более пространственных задач консолидации в виде простейших зависимостей, таблиц или графиков очень ограниченное число. Имеются решения для случая приложения к поверхности двухфазного грунта сосредоточенной силы (В…
Источник
Детальная разбивка кривых
В качестве исходной информации задаются следующие данные:
1. Направление исходной трассы дороги.
2. Положение вершины угла поворота.
3. Значения угла и радиусаRповорота.
На первом этапе, по этим данным находят главные элементы кривой (длина кривой К, тангенсы Т, биссектриса Б, домер Д). Для этой цели используются известные формулы или таблицы детальной разбивки кривых.
Над вершиной угла устанавливается в рабочее положение теодолит и от направления исходной трассы откладывается заданный угол поворота и с помощью вешки фиксируется направление трассы дороги после поворота.
От вершины угла (ВУ) с помощью рулетки откладываются в переднем и заднем направлении отрезки, равные тангенсам, и с помощью колышков закрепляются точки начала кривой (НК) и конца кривой (КК).
С использованием известных значений угла поворота , вычисляется угол по формуле
Таким образом находится направление биссектрисы угла , которое фиксируется с помощью вехи. От вершины угла в этом направлении с помощью рулетки откладывается расстояние, равное биссектрисеБ, и колышком фиксируется точка середины кривой (СК).
На этом заканчивается разбивка основных элементов кривой и приступают к детальной разбивке, которая выполняется двумя способами:
1. Способом прямоугольных координат.
2. Способом продолженных хорд.
Способ прямоугольных координат
Направление НК – ВУ принимается за ось абсцисс, причем ее начало располагается в точке НК. Перпендикулярное направление от НК к центру условной окружности с радиусом Rпринимается за ось ординат (рис. 1.5).
Рис. 1.5. Схема к разбивке кривой способом прямоугольных координат
Координаты точки 1на кривой находятся по формуле:
Здесь 
Координаты точки 2находятся по формуле:
Таким же образом находятся координаты всех точек, лежащих на участке кривой от НК до СК.
Вторая часть кривой строится аналогично, но за ось абсцисс в этом случае принимается направление КК – ВУ, а за ось ординат принимается перпендикулярное направление от точки КК к центру условной окружности.
Критерием качества выполненной работы является точное схождение двух полученных частей кривой к точке СК.
Способ продолженных хорд
Выбор системы координат и определение положения точки 1производится аналогично предыдущему способу.
Далее, с помощью рулетки измеряется длина отрезка НК – 1(этот отрезок является хордойsэлементарной дуги кривойk) и по продолжению этой хорды откладывается отрезок такой же длиныs(рис. 1.6).
В результате получают вспомогательную точку 2. Окончательное положение точки2получают способом линейной засечки: от точки1откладывается дуга радиусомs, а от точки2дуга радиусом, вычисляемым по формуле
Далее с помощью рулетки измеряется расстояние от точки 1до точки2, продолжается на такое же расстояние, фиксируется вспомогательной точкой3, затем способом линейной засечки находится окончательное положение точки3.
Рис. 1.6. Схема к разбивке кривой способом продолженных хорд
Таким образом находится положение всех точек на участке кривой от НК до СК.
Вторая часть кривой строится аналогично от точки КК к точке СК. Критерием правильности построений является точное схождение двух частей кривой к точке СК.
Недостатком этого способа является возможное накопление ошибок.
Источник

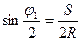 (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.
(из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.