Способы детальной разбивки кривой геодезия

Разбивка кривых на местности.

Середину кривой СК закрепляют, отложив от ВУ по направлению биссектрисы отрезок, равный Б (или Б_с).

На новом после вершины угла направлении трассы откладывают величину домера, после чего продолжают разбивку пикетажа. Обеим точкам домера (его началу и концу) присваивают одно и то же пикетажное наименование, благодаря чему пикетаж точки КК совпадает с пикетажем, считаемым по кривой.

Положение начала кривой НК и конца кривой КК определяют, используя разбитый пикетаж. Например, если ПК НК = 5 + 39,27, то от пикета № 5 откладывают вперёд 39,27 м и здесь колышком и сторожком закрепляют точку НК.

Детальная разбивка кривых. При детальной разбивке кривую закрепляют на местности через 10 или 20 м, применяя разные способы.

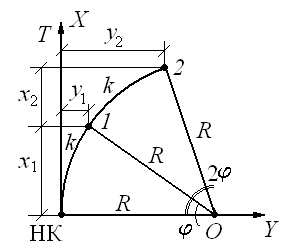
Способ ординат от касательной для круговой кривой. Для каждой точки i (рис. 15.7, а), задавая расстояние k от начала кривой, вычисляют ее координаты:

Здесь угол j выражен в радианах и равен j = k/R.

Разбивку кривой ведут от ее начала и от конца к середине. Мерной лентой по оси x откладывают длину кривой k, от полученной точки отступают назад на величину k–x и здесь строят перпендикуляр – ординату y. Значения k–x и y обычно выбирают из таблиц для разбивки кривых.

Рис. 15.7 Детальная разбивка кривых:

а – способом ординат от касательной для круговой кривой;

б – то же, для переходной и следующей за ней круговой кривой;

в – разбивка кривой электронным тахеометром

Способ ординат от касательной для переходной и следующей за ней круговой кривой (рис. 15.7, б). Для точек, расположенных в пределах переходной кривой, то есть при k £ l, координаты x, y вычисляют по формулам (15.8) и (15.9), принимая s = k. Для точек i, расположенных на круговой кривой, где k > l, вычисления выполняют по формулам:

Действия при разбивке кривой на местности аналогичны тем, что выполняют при разбивке круговой кривой.

Разбивка кривой с помощью электронного тахеометра. Выбирают на местности такую точку T (рис. 15.7, в), где обеспечена видимость точек будущей кривой и ее начала НК. В точке НК измеряют угол g и расстояние d. Вычисляют координаты точки Т:

По приведенным выше формулам вычисляют координаты точек кривой x_i, y_i (i = 1, 2, …).

Электронный тахеометр устанавливают в точке Т. Зная координаты точек Т, НК и i, вычисляют разбивочные элементы — углы b_i и расстояния d_i. Построив тахеометром вычисленные углы и расстояния, находят и закрепляют положение точек кривой на местности.

Оставьте свой комментарий

Оставить комментарий от имени гостя

Комментарии

Закрепленные

Понравившиеся

Последние материалы

Заключение (Грунты)

При построении курса учитывалась необходимость его использования для различных гидротехнических специальностей и специализаций. В качестве основной части для студентов всех гидротехнических специальностей следует считать обязательным прочтение гл. 1—7. В гл. 8.

Представления о решении задач нелинейной механики грунтов

На современном этапе развития нелинейного направления механики грунтов оформились два основных подхода к решению практических задач расчета грунтовых оснований и сооружений: нелинейно-упругий и упругопластический (А. К. Бугров, С. С. Вялов.

Прочность грунтов при сложном напряженном состоянии

Для сред и материалов, обладающих сплошностью, предложено много различных условий прочности. Для оценки прочности грунтов наиболее широкое распространение получило условие Мора—Кулона (2.38), не содержащее промежуточного главного напряжения а2 и тем.

Основные закономерности татического деформирования грунтов

За последние 15. 20 лет в результате многочисленных экспериментальных исследований с применением рассмотренных выше схем испытаний получены обширные данные о поведении грунтов при сложном напряженном состоянии. Поскольку в настоящее время в…

Упругопластическое деформирование среды и поверхности нагружения

Деформации упругопластических материалов, в том числе и грунтов, состоят из упругих (обратимых) и остаточных (пластических). Для составления наиболее общих представлений о поведении грунтов при произвольном нагружении необходимо изучить отдельно закономерности…

Описание схем и результатов испытаний грунтов с использованием инвариантов напряженного и деформированного состояний

При исследовании грунтов, как и конструкционных материалов, в теории пластичности принято различать нагружение и разгрузку. Нагружением называют процесс, при котором происходит нарастание пластических (остаточных) деформаций, а процесс, сопровождающийся изменением (уменьшением)…

Инварианты напряженного и деформированного состояний грунтовой среды

Применение инвариантов напряженного и деформированного состояний в механике грунтов началось с появления и развития исследований грунтов в приборах, позволяющих осуществлять двух- и трехосное деформирование образцов в условиях сложного напряженного состояния…

О коэффициентах устойчивости и сопоставление с результатами опытов

Так как во всех рассмотренных в этой главе задачах грунт считается находящимся в предельном напряженном состоянии, то все результаты расчетов соответствуют случаю, когда коэффициент запаса устойчивости к3 = 1. Для…

Давление грунта на сооружения

Особенно эффективны методы теории предельного равновесия в задачах определения давления грунта на сооружения, в частности подпорные стенки. При этом обычно принимается заданной нагрузка на поверхности грунта, например, нормальное давление р(х), и…

Несущая способность оснований

Наиболее типичной задачей о предельном равновесии грунтовой среды является определение несущей способности основания под действием нормальной или наклонной нагрузок. Например, в случае вертикальных нагрузок на основании задача сводится к тому…

Процесс отрыва сооружений от оснований

Задача оценки условий отрыва и определения требуемого для этого усилия возникает при подъеме судов, расчете держащей силы «мертвых» якорей, снятии с грунта морских гравитационных буровых опор при их перестановке, а…

Решения плоской и пространственной задач консолидации и их приложения

Решений плоской и тем более пространственных задач консолидации в виде простейших зависимостей, таблиц или графиков очень ограниченное число. Имеются решения для случая приложения к поверхности двухфазного грунта сосредоточенной силы (В…

Источник

Детальная разбивка кривых

В качестве исходной информации задаются следующие данные:

1. Направление исходной трассы дороги.

2. Положение вершины угла поворота.

3. Значения угла и радиусаRповорота.

На первом этапе, по этим данным находят главные элементы кривой (длина кривой К, тангенсы Т, биссектриса Б, домер Д). Для этой цели используются известные формулы или таблицы детальной разбивки кривых.

Над вершиной угла устанавливается в рабочее положение теодолит и от направления исходной трассы откладывается заданный угол поворота и с помощью вешки фиксируется направление трассы дороги после поворота.

От вершины угла (ВУ) с помощью рулетки откладываются в переднем и заднем направлении отрезки, равные тангенсам, и с помощью колышков закрепляются точки начала кривой (НК) и конца кривой (КК).

С использованием известных значений угла поворота , вычисляется угол по формуле, находится полуугол/2 и с помощью теодолита это значение откладывается от направления ВУ – НК.

Таким образом находится направление биссектрисы угла , которое фиксируется с помощью вехи. От вершины угла в этом направлении с помощью рулетки откладывается расстояние, равное биссектрисеБ, и колышком фиксируется точка середины кривой (СК).

На этом заканчивается разбивка основных элементов кривой и приступают к детальной разбивке, которая выполняется двумя способами:

1. Способом прямоугольных координат.

2. Способом продолженных хорд.

Способ прямоугольных координат

Направление НК – ВУ принимается за ось абсцисс, причем ее начало располагается в точке НК. Перпендикулярное направление от НК к центру условной окружности с радиусом Rпринимается за ось ординат (рис. 1.5).

Рис. 1.5. Схема к разбивке кривой способом прямоугольных координат

Координаты точки 1на кривой находятся по формуле:

Здесь ;k= 5, 10 или 20 м (принимается в зависимости от величины радиусаR, например, дляR 500 мk= 20 м);– радиан,= 57,3.

Координаты точки 2находятся по формуле:

Таким же образом находятся координаты всех точек, лежащих на участке кривой от НК до СК.

Вторая часть кривой строится аналогично, но за ось абсцисс в этом случае принимается направление КК – ВУ, а за ось ординат принимается перпендикулярное направление от точки КК к центру условной окружности.

Критерием качества выполненной работы является точное схождение двух полученных частей кривой к точке СК.

Способ продолженных хорд

Выбор системы координат и определение положения точки 1производится аналогично предыдущему способу.

Далее, с помощью рулетки измеряется длина отрезка НК – 1(этот отрезок является хордойsэлементарной дуги кривойk) и по продолжению этой хорды откладывается отрезок такой же длиныs(рис. 1.6).

В результате получают вспомогательную точку 2. Окончательное положение точки2получают способом линейной засечки: от точки1откладывается дуга радиусомs, а от точки2дуга радиусом, вычисляемым по формуле

Далее с помощью рулетки измеряется расстояние от точки 1до точки2, продолжается на такое же расстояние, фиксируется вспомогательной точкой3, затем способом линейной засечки находится окончательное положение точки3.

Рис. 1.6. Схема к разбивке кривой способом продолженных хорд

Таким образом находится положение всех точек на участке кривой от НК до СК.

Вторая часть кривой строится аналогично от точки КК к точке СК. Критерием правильности построений является точное схождение двух частей кривой к точке СК.

Недостатком этого способа является возможное накопление ошибок.

Источник

8.4. Детальная разбивка кривых

Для выноса трассы на местность трех главных точек кривой обычно бывает недостаточно. Необходимо построить некоторое число дополнительных точек.

Количество этих точек зависит от радиуса кривой. Для кривых радиуса менее 100 м расстояние между этими точками – 5 м, при радиусах 100-200 м – 10 м, более 500 м – 20 м. Рассмотрим три наиболее распространенных способа детальной разбивки кривой.

Способ прямоугольных координат. За начало координат условной системы принимают начало кривой НК, а ось абсцисс – тангенс Т (рис. 8.11) с положительным направлением к вершине угла.

Рис. 8.11. Способ прямоугольных координат

Координаты точек кривой P₁, P₂, и т.д. вычисляют по формулам:

, , (8.22)

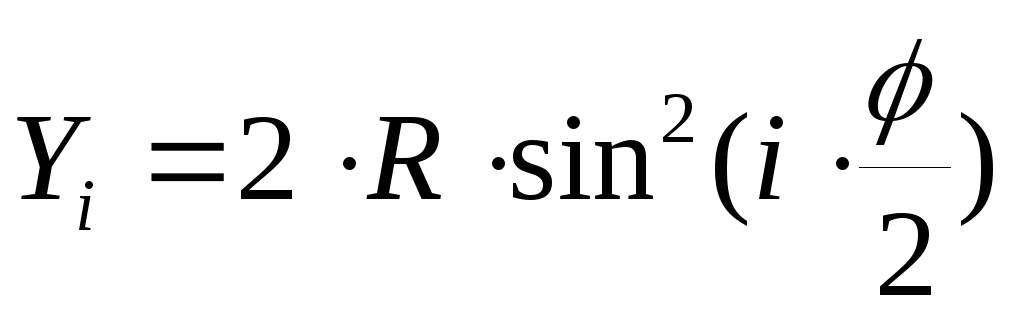
где i – номера точек, ,k — длина элементарной кривой, π = 3,1415926.

Преимущество этого способа состоит в том, что каждая точка строится независимо от предыдущей, что исключает накопление погрешностей. Но этот способ затруднительно применять в стесненных условиях.

Полярный способ. При этом способе кривая разбивается через S м, считая это расстояние по хорде. Вычисляют соответствующий заданной хорде S центральный угол φ по формуле:

( 8.23)

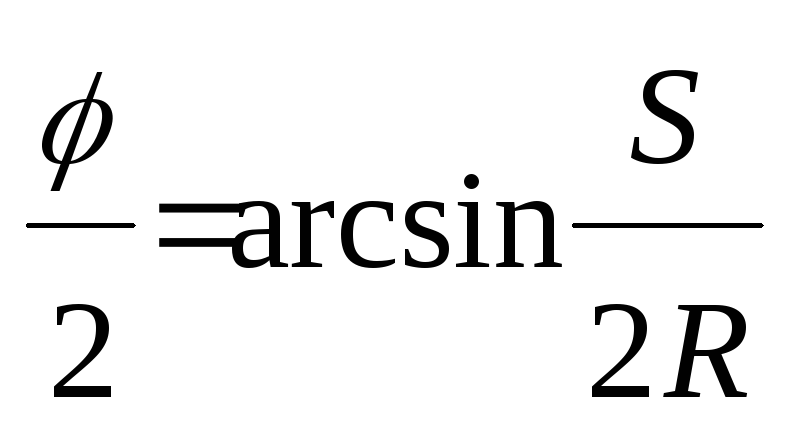
Устанавливают теодолит в начале кривой НК и от тангенса Т задают угол (рис. 8.12). Вдоль направления визирного луча откладывают лентой длину хорды, конец которой определяет положение первой точки, далее наводят зрительную трубку теодолита под угломφ к тангенсу Т. Закрепив в первой точке задний конец ленты, поворачивают ее вправо до тех пор, пока ее передний конец не попадет в перекрестие нитей сетки трубы, в этом месте фиксируют вторую точку, затем откладывают угол 3/2 φ и т.д.

Например, необходимо построить кривую радиусом R = 150 м. При этом расстояние между точками необходимо принять S = 10 м.

По формуле (8.23) определяют угол ,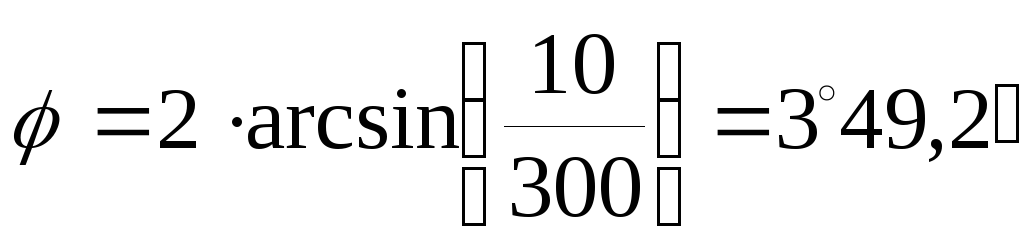

далее разбивают кривую, как описано выше.

Рис. 8.12. Полярный способ

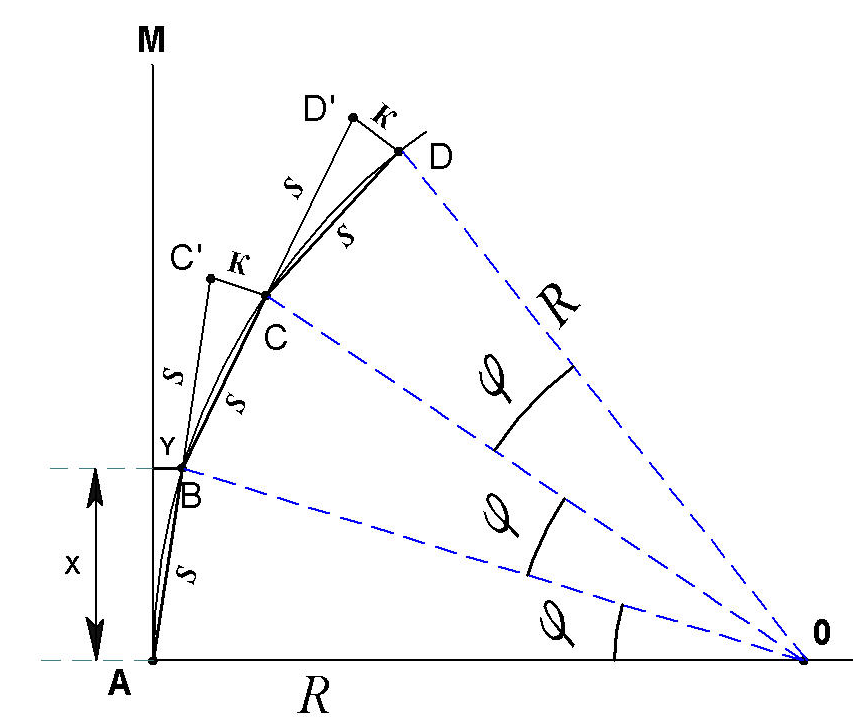
Способ продолженных хорд. Задавшись длиной хорды S кривой радиуса R вычисляют угол по формуле (8.23), затем определяют координату точки В (рис. 8.13) по формулам:

, ,. (8.24)

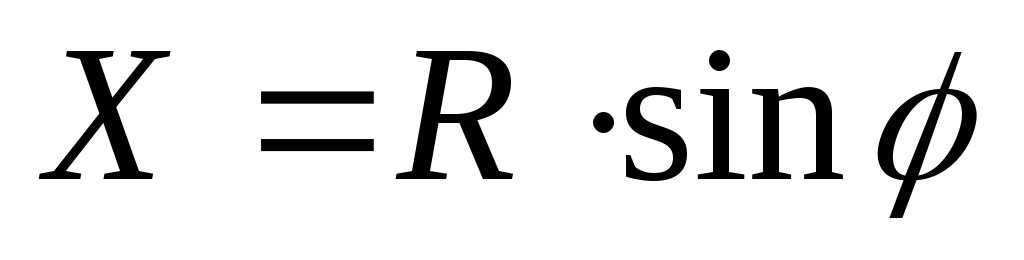
Откладывают с помощью рулетки эти значения и закрепляют ее на местности.

Рис. 8.13. Способ продолженных хорд

Затем по продолжению первой хорды откладывают отрезок S и закрепляют, полученную точку С. Удерживая задний конец ленты, в точке В, определяют положение точки с линейной засечкой радиусами S лентой и величиной k (рулеткой).

Вновь откладывают отрезок S, но уже от точки С вдоль направления второй хорды и т.д.

8.5. Составление профилей

Для составления продольного и поперечного профилей трассы и определения отметок реперов, устанавливаемых вдоль трассы, проводят техническое нивелирование с использованием нивелира типа Н3 или Н10.

Нивелирование по ходу обычно ведут методом из середины, соблюдая равенство плеч «на глаз», отсчет по рейке при этом берут по черной и красной сторонам, а по рейкам установленным на промежуточных точках (плюсовые точки, поперечники) только по черной стороне. Превышения между связующими точками определяют по черной и красной сторонам рейки. Полевой контроль нивелирования производят на станции и в ходе между реперами с известными отметками. Расхождение между превышениями, полученными на станции не должно превышать 5 мм.

На трассе дороги могут быть расположены сооружения: участковые станции, разъезды и др., мосты, трубы, поселки, водоотводящие устройства и др. Съемка таких участков ведется тахеометрическим способом с опорой на точки трассы.

Съемку узкой полосы вдоль трассы ведут по поперечным профилям, разбиваемым на пикетах и плюсовых точках трассы.

По окончании полевых работ материалы трассирования обрабатывают: проверяют полевые журналы, уравнивают нивелированные и теодолитные хода, вычисляют отметки и координаты точек трассы, составляют план, продольный и поперечный профили, поперечные профили участков дороги.

Продольный профиль разбитой на местности трассы — основной документ, полученный в результате изысканий. Им постоянно пользуются при проектировании и строительстве автомобильной дороги, а также в процессе эксплуатации. Профиль составляют в масштабе: горизонтальном 1:5000, 1:2000; вертикальном соответственно 1:500, 1:200.

Установление положения автодороги в продольном профиле по отношению к поверхности земли (или, иначе нанесение проектной линии) производится при выполнении ряда технических условий, главным из которых является соблюдение предельного (руководящего) уклона (табл. 8.1).

Положение дороги в профиле определяется также рядом точек, строго фиксированных по высоте: начало и конец трассы, ее пересечение с существующими дорогами, высота проектной линии над поверхностью воды при переходе через водотоки.

От этих точек называемых контрольными и начинают нанесение проектной линии на профиль.

Порядок построения профиля

1. Производят разграфку профильной сетки согласно рис. 8.14.

2. В графе расстояний откладывают в масштабе 1:2000 пикеты и плюсовые точки. Если между пикетами нет плюсовых точек, то расстояние 100 м не пишут. При наличии плюсовых точек указывают расстояние от пикета до плюсовой точки, либо между плюсовыми точками.

Например, между ПК0 и ПК1 находится плюсовая точка +78. Это расстояние в масштабе 1:2000 откладывают от ПК0, проводят ординату и записывают два расстояния: 78 и 22 м (т.е. расстояния точки от предыдущего и до следующего пикетов).

3. Над пикетами и плюсовыми точками, в графе фактические отметки, выписывают вычисленные отметки, предварительно округлив до сотых долей метра.

4. От линии профильной сетки (линии условного горизонта) в масштабе 1:200 на перпендикулярах к ней откладывают фактические отметки всех точек полученных в результате нивелирования из графы отметки земли.

Для того чтобы не откладывать на перпендикулярах большие расстояния, линии условного горизонта придают отметку меньше минимальной на несколько метров, например, наименьшая отметка земли 88,77 м, условная отметка 80,00 м (см. рис. 7.14). В этом случае откладывают отметки точек профиля как разности отметок земли и условного горизонта.

Точки, полученные в результате построения, соединяют между собой прямыми линиями и получают профиль местности.

5. По данным пикетажного журнала заполняют графы «грунты» и «план трассы».

Для заполнения графы «план трассы» по середине ее проводят линию и, пользуясь пикетажным журналом, строят контур местности.

6. Справа от продольного профиля трассы дороги строят один над другим поперечные профили. Горизонтальный вертикальный масштаб поперечных профилей 1:200.

7. Пользуясь пикетажными обозначениями начала и конца кривой, приведенными в пикетажном журнале заполняют графу «прямые и кривые», в этой графе проводят горизонтальную линию, изображающую ось дороги. Рассчитанные для кривых пикетажные значения НК и КК откладывают (в масштабе 1:2000) на линии пикетажа, отмечая их перпендикулярами, опущенными от этой линии на проведенную ось дороги. Вдоль перпендикуляров записывают расстояния от начала или конца кривой до ближайшего заднего или переднего пикетов.

Кривые условно обозначают скобами, обращенными при поворотах трассы вправо – выпуклостью вверх, а при поворотах ее влево — выпуклостью вниз, скобы делают высотой (глубиной) 5 мм. Под каждой кривой записывают значения элементов кривой (θ, R, Т, К, Б, Д). Над серединой каждой прямой вставки трассы выписывают ее длину, а под ней – ее румб.

Для изображения километрового указателя (на ПК0) от линии пикетажа опускают вниз перпендикуляры длиной 35 мм, нижние 5 мм из которых будут служить диаметром окружности, правую половину которой при оформлении профиля закрашивают черным цветом.

Нанесение проектной линии выполняется в соответствии с техническими условиями. Последними обычно предусматривается:

а) соблюдение нулевого баланса земляных работ (равенство объема насыпей объему выемок) при минимальном их объеме;

б) соблюдение уклонов на отдельных участках проектной линии, не превышающих допустимых пределов;

в) устройство мостового перехода через реку в виде горизонтальной площадки: при этом должны учитываться уровень высоких вод и длина площадок при подходе к отверстию моста.

Проектная линия состоит, как правило, из нескольких участков с различными уклонами. Начальной проектной отметкой могут являться: отметки точки примыкания трассы к существующим или проектным сооружениям, например отметка проектируемого мостового перехода.

Принятые согласно техническим условиям уклоны должны быть выражены в целых тысячных долях (в промилях).

С учетом приведенных данных работа по нанесению проектной линии на профиль ведется в следующем порядке:

1. В графе «проектные уклоны», в местах изменения уклонов проводят ординаты (вертикальные линии), разделяющие один участок проектной линии от другого на ПК0, ПК3+44, ПК5 и ПК10. На каждом участке внутри графы чертой показывают условно знак уклона — горизонтальная линия означает нулевой уклон, если линия идет вверх — положительный уклон, вниз – отрицательный уклон.

Над чертой, посередине пишут величину уклона, а под ней расстояние на котором действует данный уклон.

2. Проектные отметки пикетов и плюсовых точек вычисляют по формуле:

, (8.25)

где — проектная отметка начала отрезка,— проектная отметкаJ— ой точки профиля, i — уклон отрезка, — горизонтальные расстоянияJ—х точек профиля от начала отрезка с данным уклоном.

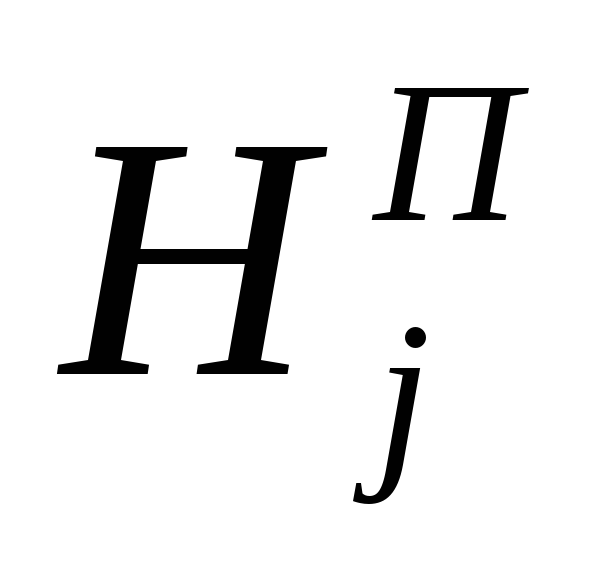
3. Вычисляют рабочие отметки (численные значения высот насыпей или глубин выемок) — как разность между соответствующими проектными и фактическими отметками.

Рабочие отметки подписывают близ точек профиля местности права от ординат, над проектной линией в случае насыпи и под проектной линией – в случае выемки.

4. Проводят вертикальные линии от точек пересечения проектной линии с линией профиля (рис. 8.15) местности (от точек нулевых работ) до линии условного горизонта и вычисляют горизонтальные расстояния от этих точек до ближайшего пикета или плюсовой точки, по формулам:

, , (8.26)

Источник