- Черчение. 10 класс
- § 9. Деление окружности на равные части
- Деление окружности на равные части
- Деление окружности на равные части
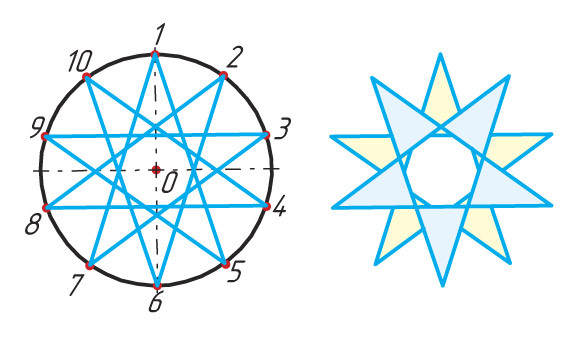
- Деление окружности на восемь равных частей
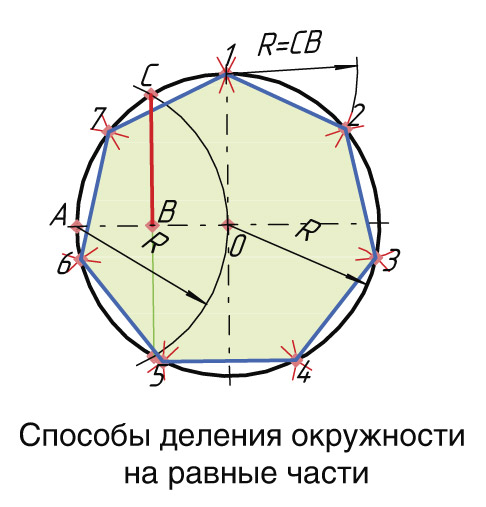
- Деление окружности на три, шесть и двенадцать равных частей
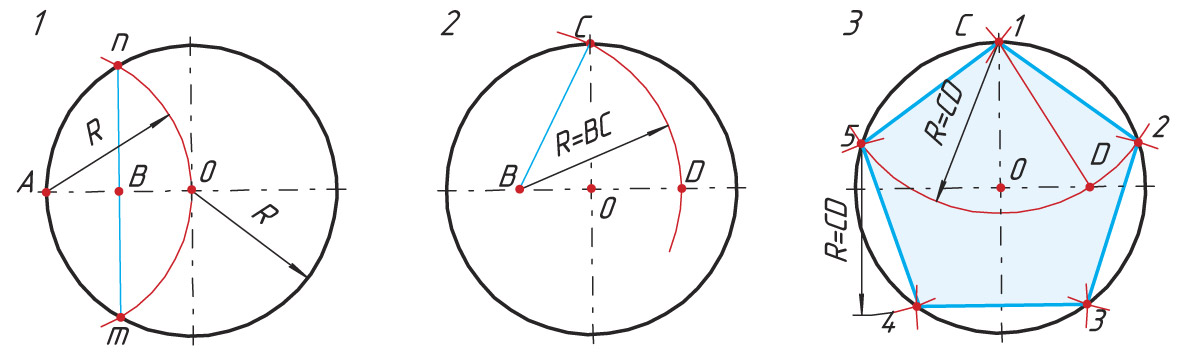
- Деление окружности на пять равных частей
- Деление окружности на семь равных частей
- Деление окружности на любое число равных частей
- Термины при построениях окружности
- Деление окружности на 4 и 8 одинаковых частей
- Деление окружности на 3 и 6 равных частей (кратные 3 трём)
- Деление окружности на 5 и 10 равных частей
- Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
- Нахождение центра дуги окружности
Черчение. 10 класс
§ 9. Деление окружности на равные части
Деление окружности на равные части
Для выполнения чертежей некоторых изделий необходимо овладеть приемами деления окружностей на равные части и построения многоугольников, вписанных в окружность (рис. 34, 35).
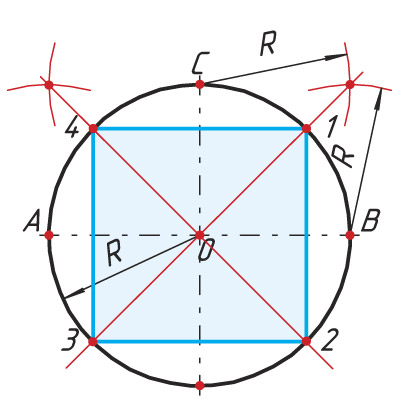
Деление окружности на 2 и 4 равные части. Любой диаметр делит окружность на две равные части. Два взаимно перпендикулярных диаметра делят ее на четыре равные части.

Последовательность деления окружности на 4 равные части
1. Проводят окружность с радиусом R.
2. Из точек С и В тем же радиусом R, что и радиус окружности, проводят дуги до их взаимного пересечения.
3. Точку пересечения соединяют прямой с центром окружности. Получают точки 1 и 3.
4. Аналогично выполняют построение из точек А и С.

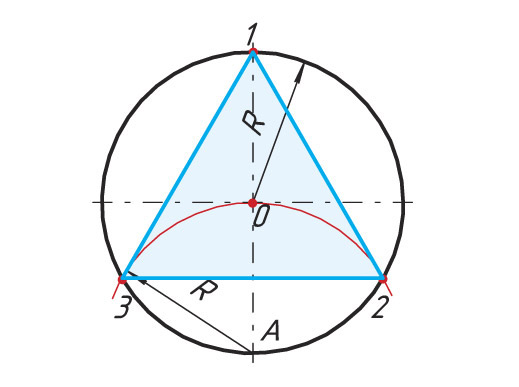
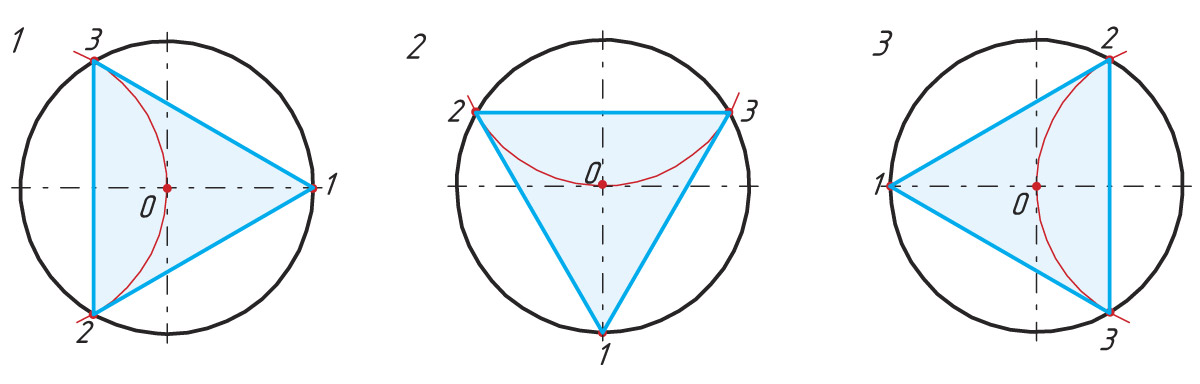
Деление окружности на 3 и 6 равных частей
Последовательность деления окружности
1. Проводят окружность с заданным радиусом R.
2. Из точки А тем же радиусом R проводят дугу до пересечения с окружностью в точках 2 и 3.
3. Точки пересечения 2 и 3 соединяют прямыми
линиями, получают вписанный треугольник.

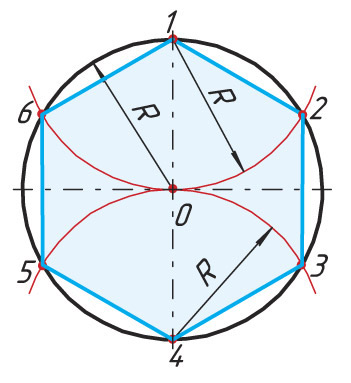
При делении окружности на 6 равных частей выполняется то же построение, что и при делении окружности на 3 части, но дугу описывают не один, а два раза, из точек 1 и 4 радиусом окруж ности R.
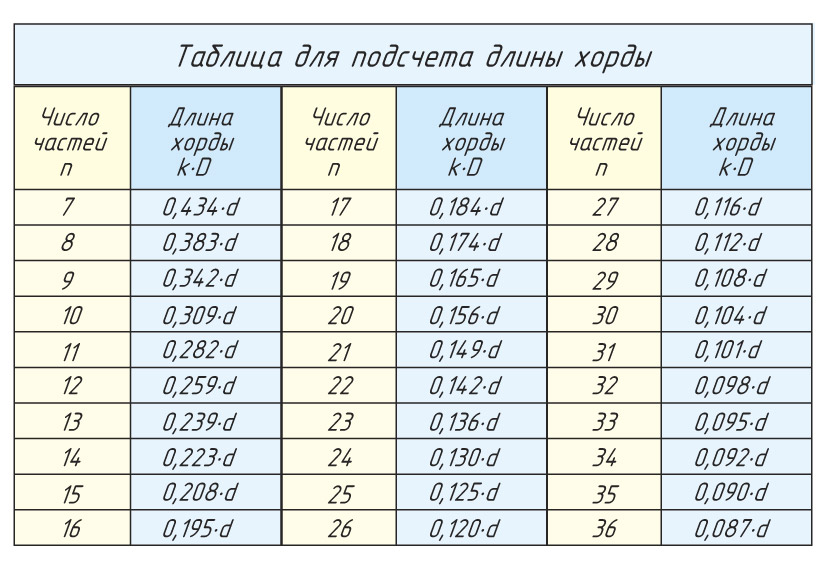
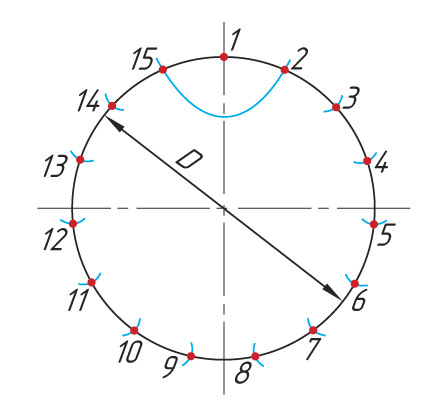
Выполнять деление окружности на равные части можно не только с помощью циркуля, но и используя угольник. Разделить окружность на число частей n можно, используя формулу расчета длины хорды (см. Памятку 4).
| Памятка 4. Деление окружности на равные части | |
| При помощи угольников | |
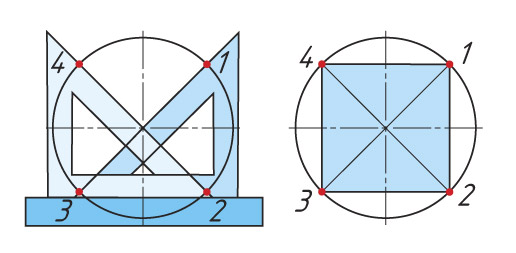 | 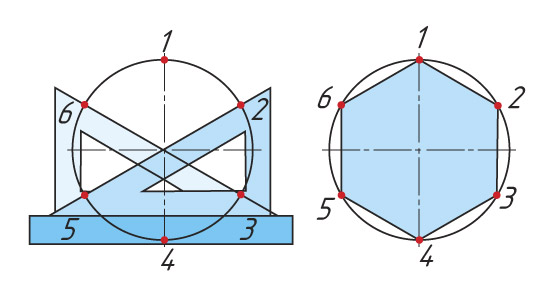 |
| Угольником с углом 45°. Гипотенуза угольника должна проходить через центр окружности | 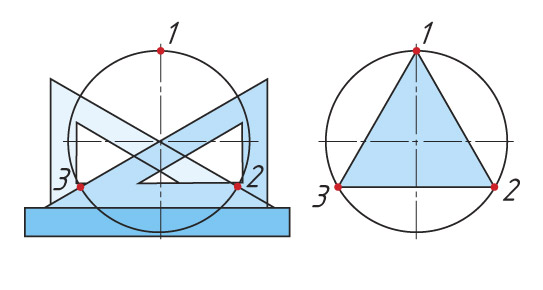 |
| Таблица коэффициентов для подсчета длины хорды | |
 |  |


 Знаете ли вы, что не все кривые линии могут быть вычерчены с помощью циркуля и их построение выполняется по ряду точек? При вычерчивании кривой полученный ряд точек соединяют по лекалу, поэтому ее называют лекальной кривой линией. Точность построения лекальной кривой повышается с увеличением числа промежуточных точек на ее участке. К лекальным кривым относятся эллипс, парабола, гипербола, которые получаются в результате сечения кругового конуса плоскостью.
Знаете ли вы, что не все кривые линии могут быть вычерчены с помощью циркуля и их построение выполняется по ряду точек? При вычерчивании кривой полученный ряд точек соединяют по лекалу, поэтому ее называют лекальной кривой линией. Точность построения лекальной кривой повышается с увеличением числа промежуточных точек на ее участке. К лекальным кривым относятся эллипс, парабола, гипербола, которые получаются в результате сечения кругового конуса плоскостью. 









