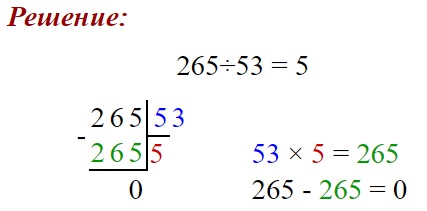Способы деления двухзначных чисел

Алгоритмы устных способов деления двузначных и трёхзначных чисел
консультация по математике (3 класс) на тему

Для успешного овладения учащимися 3-4 классов устным счётом я составила свои алгоритмы для некоторых случаев деления двузначных и трёхзначных чисел методом подбора.

Скачать:

Вложение	Размер
algoritmy.docx	14.28 КБ

Предварительный просмотр:

Для успешного овладения учащимися 3-4 классов устным счётом я составила свои алгоритмы для некоторых случаев деления двузначных и трёхзначных чисел методом подбора.

Алгоритмы устных способов деления двузначных и трёхзначных чисел

Алгоритм вычисления вида 48 : 2
Для того чтобы вычислить выражение вида 48 : 2, надо:
1) разделить единицы на делитель;
2) разделить десятки на делитель;
3) сложить полученные частные;
4) оформить результат вычисления.
Например: 48 : 2 = (8+40) : 2 = 8 : 2 + 40 : 2 = 4+20 = 24.

Алгоритм вычисления вида 57 : 3

Для того чтобы вычислить выражение вида 57 : 3, надо:
1) разделить единицы на делитель;
2) число 7 на 3 не делится, занимаем десяток;
3) число 17 на 3 не делится, занимаем ещё десяток;
4) число 27 на 3 делится, ответ 9;
5) разделить десятки на делитель, два занимали, осталось три десятка; 30 на 3 делится, ответ 10;
6) сложить полученные частные;
7) оформить результат вычисления.

Например: 57 : 3 = (27+30) : 3 = 27 : 3 + 30 : 3 = 9+10 = 19.

Алгоритм деления двузначного числа на двузначное число вида 72 : 18

Для того, чтобы разделить двузначное число на двузначное методом подбора, надо:
1) определить количество цифр в частном, при делении десятков на десятки получаются единицы, значит, в частном будет одна цифра;
2) делим единицы на единицы;
3) число 2 на 8 не делится, занимаем десяток;
4) число 12 на 8 не делится, занимаем ещё десяток;
5) число 22 на 8 не делится, занимаем ещё десяток;
6) число 32 на 8 делится, ответ 4;
5) делим десятки на десятки, 3 занимали, осталось 4 десятка; 4 на 1 делится, ответ тоже 4;
6) сравниваем полученные ответы, они совпадают, следовательно частное определено верно;
7) делаем проверку.

Алгоритм деления двузначного числа на двузначное число вида 75 : 25

Для того, чтобы разделить двузначное число на двузначное методом подбора, надо:
1) определить количество цифр в частном, при делении десятков на десятки получаются единицы, значит в частном будет одна цифра;
2) делим единицы на единицы;
3) число 5 на 5 делится, ответ 1;
4) делим десятки на десятки, 7 на 2 не делится без остатка, значит ответ 1 не верный;
5) занимаем десяток, число 15 на 5 делится, ответ 3;
6) делим десятки на десятки, один занимали, осталось 6 десятков, 6 на 2 делится, ответ 3;
7) сравниваем полученные ответы, они совпадают, следовательно частное определено верно;
8) делаем проверку.

Алгоритм деления трёхзначного числа на двузначное число вида 196 : 28

Для того, чтобы разделить трёхзначное число на двузначное методом подбора, надо:
1) определить количество цифр в частном, в частном будет одна цифра;
2) делим единицы на единицы, число 6 на 8 не делится, занимаем десяток;
3) число 16 на 8 делится, ответ 2;
4) делим десятки на десятки, один занимали, осталось 18 десятков, 18 на 2 делится, ответ 9;
5) сравниваем полученные ответы, они не совпадают, следовательно, частное определено не верно;
6) делим единицы на единицы, число 6 на 8 не делится, занимаем десятки;
7) 56 на 8 делится, ответ 7;
8) делим десятки на десятки, пять занимали, осталось 14, 14 на 2 делится, ответ 7.
9) сравниваем полученные ответы, они совпадают, следовательно частное определено верно;

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

На уроке научимся делить столбиком на двузначное число без остатка и с остатком, повторим единицы массы, будем решать задачи.

Ребята, делить столбиком на двузначное число совсем непросто! Потребуется серьезная разминка. Проверим, кто из вас отлично знает таблицу умножения и деления. Решите примеры устно, найдите ответ и соответствующую ему букву. Запишите числа в таблицу в порядке возрастания. Какое слово получилось? Прочитайте.

Правильный ответ найдете в рубрике «Это интересно!».

Письменное деление на двузначное число

Что нужно знать и уметь, чтобы хорошо научиться делить на двузначное число? Подумайте, ребята!

Конечно, надо знать назубок таблицу умножения – это первое. А второе – уметь делить на однозначное число столбиком (уголком).

Давайте вспомним алгоритм деления на однозначное число.

Решите самостоятельно примеры уголком и проверьте себя по образцу.

А теперь рассмотрим деление уголком на двузначное число. Нам понадобится черновик. При делении на двузначное число цифру, которую мы подобрали, требуется проверить умножением. Если цифра не подошла (а такое бывает), подбираем следующую цифру, снова проверяем умножением и так далее. Все эти вычисления лучше выполнить на черновике. Например, разделим 624 на 26. Запишем пример столбиком (уголком).

Обязательно проговариваем каждый этап вычислений.

Пользуясь алгоритмом, решите самостоятельно два примера столбиком. Проговаривайте каждый этап, чтобы не допустить ошибку. Сравните с образцом.

448 : 64 952 : 34

Ребята, вы заметили, что алгоритм остается прежним? Требуется лишь больше внимания и сосредоточенности.

Попробуйте и вы, ребята, овладеть делением!

Деление на двузначное число с остатком

Действует ли при делении с остатком какой-либо другой алгоритм? Нет! При делении с остатком рассуждают точно так же, как и при делении без остатка.

Ребята, какое правило нужно знать и обязательно проверять при делении с остатком?

А теперь решите самостоятельно примеры на деление с остатком. Не забывайте сравнивать остаток с делителем, сделайте проверку.

272 : 98 495 : 46 385 : 65 321 : 47

Проверь себя.

Ребята, в каком примере вы встретили затруднение? Рассмотрим вместе пример

495 : 46

Почему в частном появился 0 (нуль)?

Первое неполное делимое 49. Делим на 46. Берем по 1. Остаток 3 меньше делителя 46. Делим верно. Сносим следующую цифру 5.

35 делим на 46. Берем по 0 (35 меньше, чем 46). Остаток 35 меньше делителя, разделили верно. Сделаем проверку, убедимся в правильности вычислений.

Уметь делить с остатком – полезный навык, который не раз поможет вам в решении практических задач. Например, для постройки одинаковых башен у вас имеется 430 деталей лего-конструктора. Сколько башен можно построить, если на каждую нужно 35 деталей? Останутся ли лишние детали?

Давайте вместе решим эту задачу.

430 разделим на 35. Сделаем это столбиком (уголком).

Мы видим, что при делении получился остаток 10. Делаем вывод: из 430 деталей лего-конструктора можно сделать 12 одинаковых башен и еще 10 деталей останется.

Разделить можно на черновике, а решение в тетради записать в строчку.

430 : 35 = 12 (ост.10) – башен можно сделать.

Ответ: 12 башен и 10 деталей останется.

Если вы хорошо умеете делить с остатком, решение можно сразу записать в тетрадь:

Решите самостоятельно практическую задачу.

Задача

Ребята 4 класса изготовили для первоклассников 126 закладок в учебники. Сколько закладок достанется каждому первокласснику, если в первом классе 25 учеников? Останутся ли лишние закладки?

Проверь себя.

Решение задач с единицами массы

Ребята, какие единицы массы вы знаете? Давайте вспомним!

Игра

В каждом столбике найди «лишнее» слово, обоснуй свой ответ.

Вспомним таблицу единиц массы.

Задача

В тепличном хозяйстве выращивают огурцы и помидоры. В первой теплице собрали 132 кг огурцов. Во второй теплице собрали 1 ц 56 кг помидоров. Урожай огурцов или помидоров богаче и на сколько килограммов?

Разберем задачу вместе.

Выразим 1 ц 56 кг в килограммах. Из таблицы видим, что 1 ц = 100 кг, значит,

1 ц 56 кг = 156 кг

156 – 132 = 14 (кг) – собрали больше помидоров, чем огурцов.

Ответ: на 14 кг больше.

Следующую задачу решите самостоятельно. Проверьте по образцу.

Задача

5 т яблок разложили в ящики по 10 кг в каждый и отправили в хранилище. 120 ящиков с яблоками развезли в магазины города. Сколько килограммов яблок осталось в хранилище.

Проверь себя.

• 5 000 : 10 = 500 (ящ.) – с яблоками отправили в хранилище.
• 500 – 120 = 380 (ящ.) – с яблоками осталось в хранилище.
• 380 ∙ 10 = 3 800 (кг) – яблок в хранилище.

Решение задачи можно записать выражением: (5 000 : 10 – 120) ∙10 = 3 800

А теперь разберем задачу, в которой встретится деление с остатком.

Задача

В хозяйстве собрали 5 ц клубники. 300 кг клубники оставили в ящиках, а остальную клубнику расфасовали в небольшие контейнеры по 300 г. Сколько контейнеров с клубникой получилось? Сколько граммов клубники осталось?

Сначала выразим 5 ц в килограммах.

Узнаем, сколько кг клубники расфасовали в контейнеры.

500 – 300 = 200 (кг) – расфасовали в контейнеры.

Выразим 200 кг в граммах.

200 кг = 200 000 г.

Разделим 200 000 на 300 столбиком.

Сделаем вывод: если в условии задачи содержатся разные единицы массы, то необходимо выразить их в одинаковых единицах.

Сегодня на уроке мы научились делить столбиком на двузначные числа с остатком и без остатка, повторили единицы массы, решали задачи.

Источник

Деление на двузначное число — способы и примеры решений

Деление на двузначное число похоже на тот же процесс с однозначным числом, но занимает больше времени. Однако есть немало методов, которые упрощают процесс. Научиться выполнять деление быстро помогут основные правила и серьезная практика.

Деление на двузначное число устно

Осуществляется такое деление методом подбора. Например, нужно разделить число 90 на двузначное число 15 без остатка.

Чтобы это сделать устно, нужно подобрать такое число, которое при умножении его на 5 (15 оканчивается на 5) даст число, оканчивающееся на 0 (так как 90 оканчивается на ноль).

Какое число при умножении на 5 даст в результате число с цифрой 0 на конце? Их несколько.

Теперь проверяем. Если цифра нам подходит, то, умножив ее на 15, получим 90:

Последняя цифра 6 подходит. Мы выполнили деление: 90 : 15 = 6.

Деление в столбик на двузначное число

Деление в столбик школьники проходят еще в младших классах на уроках математики. В дальнейшем его применяют как вспомогательное средство при решении задач. Но если не пройти в нормальном виде деление уголков, то могут возникнуть затруднения и с трехзначными числами.

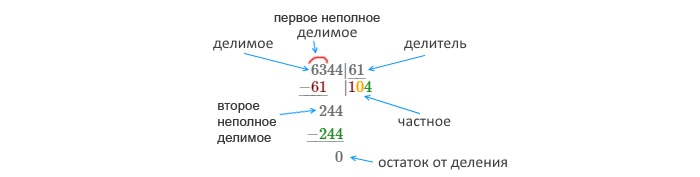
На рисунке 1 показан принцип деления и названия основных элементов процесса. Как и при делении на однозначные числа, работает алгоритм перехода от крупных к мелким единицам.

Порядок действий опишем, взяв для примера вычисление, представленное на рисунке 1:

Выделить самое маленькое двузначное число 63, которое можно поделить на делитель 61. Оно всегда больше того, которое является делителем.

Делим 63 на 61. Сколько раз 61 поместится в 63? Один. Записываем под уголком единицу. Это первая цифра частного.

Умножаем делитель на эту первую цифру: 61 * 1 = 61, вычитаем из 63 число 61, проводим черту и пишем разность — 2.

Сносим следующую цифру делимого — 4. Получаем число 24. Оно не делится на 61, потому записываем ноль на место второй цифры частного (это место рядом с цифрой 1 в нашем примере).

Сносим следующую (последнюю в нашем примере) цифру, это 4. Получаем число 244. Делим его на 61. Применим правило устного деления, описанное выше. Нужно подобрать такую цифру, которая при умножении на последнюю цифру (у 61 последняя цифра 1) даст ответ, оканчивающийся на последнюю цифру делимого (у 244 последняя цифра 4, она нам и нужна). Т. е. 4 * 1 = 4. Проверка: 61 * 4 = 244. Мы подобрали цифру 4 и она нам подошла.

Вписываем 4 третьей цифрой частного в уголок, получаем 104. Умножаем 61 на 4 и вычитаем результат из 244. Получаем 0. Деление выполнено.

В данном примере делимое — трёхзначное число. В общем случае процесс сноса цифр делимого и деления их на делитель продолжается до тех пор, пока не закончатся все цифры делимого. Этот принцип подходит для трехзначных, четырехзначных и других многозначных чисел.

Примеры деления в столбик на двузначное число

Рассмотрим некоторые примеры. Они довольно простые и помогут понять основные моменты данного способа.

Пример 1

Найдём значение частного чисел 265 и 53:

Пример 2

Найдем результат деления чисел 624 и 52:

Пример 3

Рассмотрим более сложные случаи деления в столбик. Найдем значение частного чисел 1610 и 35:

Пример 4

Деление пятизначного числа на двузначное. Узнаем значение частного чисел 10150 и 35:

Пример 5

Деление многозначного числа на двузначное с остатком. Вычислим, чему будет равно частное чисел 1978 и 38:

Деление на двузначное число можно выполнять в столбик и устно, но многозначные числа устно считать намного сложнее. Немногие школьники могут похвастаться подобными умениями.

Освоение процесса деления поможет школьникам в дальнейшем обучении. Так же существует немало тренажеров и онлайн-калькуляторов, которые можно использовать в свою пользу.

Источник