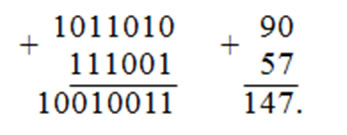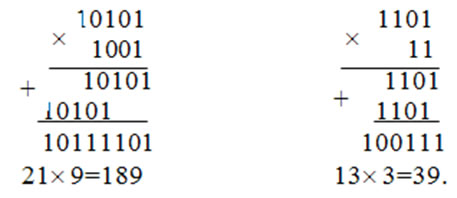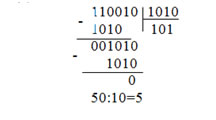Способы деления двоичных чисел

Содержание

Арифметические операции в двоичной системе
Сложение двоичных чисел.
Вычитание двоичных чисел.
Умножение двоичных чисел.
Деление двоичных чисел.
Практическая работа №5. Операция деления чисел в ЭВМ
Способы деления двоичных чисел

Арифметические операции в двоичной системе

Арифметические действия в двоичной системе производится по тем же правилам что и в десятичной системе счисления. Однако так как в двоичной системе счисления используются только две цифры 0 и 1, то арифметические действия выполняются проще, чем десятичной системе.

Сложение двоичных чисел.

Сложение выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного сложения:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10.

При сложении необходимо помнить, что 1+1 дают нуль в данном разряде и единицу переноса в старший.

Пример 3.5. Сложить два числа:

Вычитание двоичных чисел.

Вычитание выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного вычитания:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1.
Пример 3.6. Найти разность двух чисел:

Т.е. при вычитании двоичных чисел в случае необходимости занимается 1 из старшего разряда, которая равна двум единицам младшего разряда.

Умножение двоичных чисел.

Умножение в двоичной системе производится по тому же принципу что и в десятичной системе счисления, при этом используется таблица двоичного умножения:
0 * 0 = 0
0 * 1 = 0
1 * 0 = 0
1 * 1 = 1 .
Пример 3.7. Найти произведение двух чисел:

Как видно из приведенных примеров, операция умножения может быть представлена как операции сдвига и суммирования.

Деление двоичных чисел.

Деление в двоичной системе производится вычитанием делителя со сдвигом вправо, если остаток больше нуля.
Пример 3.8. Найти частное двух чисел если:
1. Делимое больше делителя:

2. Делимое меньше делителя:

Как видно из приведенных примеров, операция деления может быть представлена как операции сравнения, сдвига и суммирования.

Вернуться в оглавление:Алгоритмические языки

Источник

Практическая работа №5. Операция деления чисел в ЭВМ

Практическая работа №5

Операция деления чисел в ЭВМ

Целью работы является изучение деления чисел как с фиксированной, так и с плавающей точкой в ЭВМ.

2. Теоретическая часть

2.1. Умножение и деление чисел в двоичной системе счисления.

Наиболее просто умножение выполняется в прямом коде, независимо от того, являются ли операнды целыми или дробными числами. В ЭВМ с фиксированной точкой умножение реализуется в два этапа.

Первый этап заключается в определении знака произведения с помощью сложения знаковых цифр сомножителей по модулю два, где 0 – соответствует плюсу, а 1 – минусу.

Сложение по модулю два

По-другому, это эквивалентно

На втором этапе производится перемножение модулей сомножителей, затем в случае необходимости округления полученного модуля произведения, после чего к модулю результата приписывается его знак, определенный на первом этапе.

Умножение производится по обычным правилам арифметики, согласно двоичной таблицы умножения.

Традиционная схема умножения похожа на известную из школьного курса процедуру записи «в столбик». Вычисление произведения двух n-разрядных двоичных чисел без знака сводится к формированию частичных произведений (ЧП) по одному на каждую цифру множителя, с последующим суммированием полученных ЧП. Перед суммированием каждое частичное произведение должно быть сдвинуто на один разряд относительно предыдущего.

Деление чисел в двоичной системе производится аналогично делению десятичных чисел. Рассмотрим деление двух целых чисел, так как делимое и делитель всегда могут быть приведены к такому виду путем перенесения запятой в делимом и делителе на одинаковое число разрядов и дописывания необходимых нулей. Деление начинается с того, что от делимого слева отделяется минимальная группа разрядов, которая, рассматриваемая как число, превышает или равна делителю. Дальнейшие действия выполняются по обычным правилам, прием последняя целая цифра частного получается тогда, когда все цифры делимого исчерпаны.

2.2. Умножение двоичных чисел в ЭВМ. Машинный метод.

Умножение двоичных чисел сводится к операциям сдвига на один двоичный разряд влево и повторения первого сомножителя в тех разрядах, где второй сомножитель содержит 1, и сдвига без повторения в разрядах с 0. Сдвиг всегда чередуется со сложением, поскольку для выполнения операций имеется всего два регистра (два места для записи чисел). Другими словами, реализации отдельной операции умножения в процессоре не требуется.

Как и в операции сложения, при умножении чисел с ограниченной разрядной сеткой может возникнуть переполнение.

Перемножение двух n-разрядных двоичных чисел P=A*B приводит к получению результата, содержащего 2n битов. Таким образом, алгоритм умножения предполагает последовательное выполнение двух операций – сложения и сдвига. Суммирование ЧП обычно производится не на завершающем этапе, а по мере их получения. Это позволяет избежать необходимости хранения всех ЧП, то есть сокращает аппаратурные издержки. Устройство умножения предполагает наличие регистров множимого, множителя и суммы частичных произведений, а также сумматора ЧП и, возможно, схем сдвига (если операция сдвига не реализована иным способом).

Существуют следующие алгоритмы умножения:

1. Алгоритм сдвига вправо — начиная с младших разрядов множителя, со сдвигом суммы ЧП вправо и при неподвижном множимом.

2. Алгоритм сдвига влево — начиная со старших разрядов множителя, со сдвигом суммы ЧП влево и неподвижном множимом.

Рассмотрим пример умножения двоичных чисел в ЭВМ.

Выполнить умножение чисел A = 101112 и B = 1012 в двоичной системе счисления.

Умножение выполняется в несколько этапов:

1. Впишем множимое A, допустим в 8-ми разрядный регистр, начиная с младших разрядов (нумерация разрядов начинается с нуля). В недостающие разряды записываем нули.

2. Впишем множитель В в 8-ми разрядный регистр, начиная с младших разрядов. В недостающие разряды записываем нули.

3. Подготовим (обнулим) регистр результата C удвоенной разрядности (16 бит). Произведение содержит в два раза больше разрядов чем исходные сомножители.

4. Дальше выполняется следующий цикл:

4.1. Анализируем очередной разряд множителя В (начинаем с младших), если он «1», то прибавляем множимое A к старшим разрядам регистра С, результат снова в С. Если очередной разряд множителя «0», пропускаем данный шаг.
4.2. Сдвигаем содержимое регистра С на один разряд вправо. При этом крайний левый (старший) разряд заполняется нулем. Но если перед этим была операция сложения, во время которой возник перенос из старшего разряда, то тогда крайний левый разряд заполняется единицей.

4.3. Действия, описанные в п. п. 5.1 и 5.2,повторяютсядо тех пор не будут проанализированы все разряды множителя.

В итоге процесс умножения выглядит следующим образом:

где «+А» — числоА прибавляется к регистру C; «—>»содержимое регистра C сдвигается на один разряд вправо; «=» — показывается значение частичного произведения полученного после сложения, которое заносится в регистр С.

5. Определяется знак результата. Если знаки исходных сомножителей одинаковы, то результирующее произведение положительно и наоборот. В данном случае знаки совпадают, следовательно результирующее произведение положительно.

В итоге получается ответ:

2.3. Деление двоичных чисел в ЭВМ. Машинный метод.

Рассмотрим процесс деления двоичных чисел в ЭВМ на примере деления числаА=100101112 на B=1012, который включает следующие этапы:

1. Впишем делимое A в 16-ти разрядный регистр, начиная с младших разрядов (нумерация разрядов начинается с нуля). В недостающие разряды записываем нули.

Так как для выполнения деления требуется производить операцию вычитания, это требует использования знаковой арифметики. И поэтому в данном случае 15-й разряд является знаковым (0 — соответствует положительному числу, 1 — отрицательному), а старшим разрядом числа является 14-й разряд.

Читайте также: Способы пайки трубы пнд

2. Впишем делитель В в 16-ти разрядный регистр, начиная с младших разрядов. В недостающие разряды записываем нули.

Здесь также как и с числом A 15-й разряд является знаковым, а старшим разрядом числа является 14-й разряд. Эти знаковые разряды будут показывать нам знаки, образующихся в процессе деления, частичных остатков. Они не имеет никакого отношения к знакам исходных операндов и знаку результата, а играют чисто технологическую роль.

3. Предварительный сдвиг делителя. Сдвинем делитель B влево так, чтобы позиция старшей значащей единицы, в нем, совпала с позицией старшей значащей единицы в делимом A. Количество необходимых для этого сдвигов запомним в числе k. В нашем случае старшая значащая единица в делимом Aрасположена в 7-м разряде, a в делителе B — в 2-м разряде. Следовательно, необходимо сдвинуть число B влево на 5 разрядов (k = 5).
Сдвинутый делитель выглядит следующим образом :

4. Так как в процессе деления множитель B придется не только прибавлять но и вычитать, то нам необходимо иметь число -B. Для этого представим B в дополнительном коде.

5. Процесс деления будет следующий:

5.1. Вычитаем из делимого А делитель В (т. е. прибавляем -В).

5.2. Анализируем знак полученного частичного остатка (15-й разряд). В регистр результата записываем «0» если остаток отрицательный и единицу в противном случае. Помним, что отрицательному числу соответствует наличие единицы в 15-м разряде и наоборот.

5.3. Сдвигаем частичный остаток на один разряд влево. При этом крайний правый (младший) разряд заполняется нулем, а знаковый разряд (15-й) в процессе сдвига не участвует.

5.4. Прибавляем к частичному остатку делитель В если остаток отрицательный либо вычитаем делитель в противном случае.

5.5. Анализируем знак полученного частичного остатка (15-й разряд). В регистр результата записываем «0» если остаток отрицательный и единицу противном случае.

5.6. Действия, описанные в пунктах 5.3-5.5, выполняем k раз (если k=0, то ни разу не выполняем). Но, если после очередной операции сложения/вычитания частичный остаток, по модулю, будет меньше чем исходный (несдвинутый) делитель, то операция деления прекращается, а частное дополняется нулями так, чтобы число разрядов частного равнялось k+1.

В итоге процесс деления для вышеуказанного примера будет выглядеть следующим образом:

Источник

Способы деления двоичных чисел

ДЕЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ

Если умножение выполняется путем многократных сдвигов и сложений, то деление, будучи операцией обратной умножению,— путем многократных сдвигов и вычитаний.

(ПРАВИЛЬНЫЕ ДРОБИ, БЕЗ ЦЕЛОГО.)

При представлении чисел с фиксированной запятой деление возможно, если делимое по модулю меньше делителя, в противном случае произойдет переполнение разрядной сетки .

Так же, как и при «ручном» делении, разряды частного при делении чисел на машине определяются (начиная со старшего) путем последовательного вычитания делителя из остатка, полученного от предыдущего вычитания. Однако здесь операция вычитания заменяется операцией сложения остатка с отрицательным делителем, представленным в обратном или дополнительном коде. Знак частного определяется сложением по модулю два кодов знаков делимого и делителя.

Рассмотрим сначала пример деления «ручным» способом.

Здесь после каждого вычитания делитель сдвигается вправо по отношению к делимому. Если остаток после вычитания получился положительный, в разряд частного записывается 1, если отрицательный — нуль. На практике обычно отрицательный остаток не записывается, просто делитель сдвигается дополнительно на один разряд вправо и вычитается из положительного остатка.

В машинах вместо сдвига делителя вправо осуществляется сдвиг остатка влево, что, по сути, ничего не изменяет.

При делении с восстановлением остатка отрицательный остаток восстанавливается суммированием с положительным делителем. Восстановленный остаток сдвигается влево на один разряд. Из сдвинутого остатка вновь вычитается делитель. По знаку полученного остатка определяется цифра очередного разряда частного. Процесс деления продолжается до получения заданного числа цифр частного, обеспечивающего необходимую точность результата.

Посмотрим, как решается предыдущий пример на машине.

Процесс деления начинается со сдвига делимого влево на один разряд, после чего к нему прибавляется делитель, представленный, например, в дополнительном модифицированном коде:

Очевидно, что при делении с восстановлением остатка в самом неблагоприятном случае для формирования каждого разряда частного требуется выполнить две операции: вычитания (сложения в дополнительном или обратном коде) и сложения (восстановления остатка). То есть время выполнения операции деления может оказаться в два раза больше по сравнению с минимально возможным.

Для сокращения среднего времени выполнения операции деления реализуют деление без восстановления остатка, алгоритм которого следующий.

1) Определить знак частного суммированием по модулю два содержимых знаковых разрядов делимого и делителя.

2) Из делимого вычесть делитель. Если остаток отрицательный, перейти к пункту 3. В противном случае вычисление закончить (произошло переполнение).

3) Запомнить знак остатка.

4) Сдвинуть остаток на один разряд влево.

5) Присвоить делителю знак, обратный знаку остатка, запомненному в п. 2.

6) Сложить сдвинутый остаток и делитель (с учетом знака).

7) Присвоить цифре частного значение, противоположное коду знака остатка.

8) Повторять выполнение пунктов 3—7 до тех пор, пока не будет обеспечена требуемая точность вычисления частного.

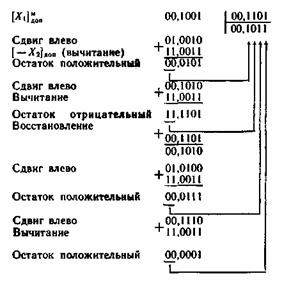
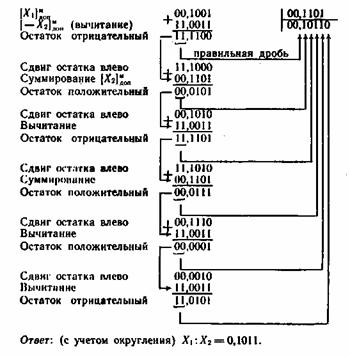
Решение рассмотренного выше примера в данном случае осуществляется по следующей схеме:

С ПЛАВАЮЩЕЙ ЗАПЯТОЙ

При выполнении операции деления над числами с ПЛАВАЮЩЕЙ ЗАПЯТОЙ мантисса частного определяется как результат деления мантиссы делимого на мантиссу делителя, а порядок частного в результате вычитания кода порядка делителя из кода порядка делимого, так как

Деление целых ненулевых n-разрядных (не считая знаковых разрядов) чисел А:В, представленных в прямом (для простоты) коде, приводит к получению целого частного С и целого остатка 0, которому присваивается знак делимого; знак частного вычисляется как сумма по модулю два операндов А и В.

Деление выполняется в следующей последовательности.

1) Делитель В сдвигается влево (нормализуется), так чтобы в старшем информационном разряде оказалась 1;подсчитывается количество сдвигов S; частное от деления может быть не более (S + 1) разрядов, не равных нулю.

2) Выполняется (S+1) цикл деления модулей |А| на IB’l где В» — нормализованное В, в результате находится(S+ 1) разряд частного, начиная со старшего из (S+ 1)младших.

3) Полученный в последнем цикле деления остаток Rs+1, если он положительный, сдвигается вправо на S разрядов; если же Rs+1

Частному и остатку присваиваются знаки.

Деление двоичных чисел основывается на последовательном вычитании делителя из разрядов делимого и остатка от деления. Таким образом, деление реализуется с помощью операций сдвига, вычитания и анализа результата вычитания. По аналогии с умножением здесь целесообразно осуществлять деление чисел без знаков, а знак частного определять отдельно на основе анализа знаков операндов. Перед выполнением деления необходимо убедиться, что делитель не равен нулю.

Деление двоичных чисел, представленных в форме с фиксированной запятой, сводится к последовательности операций вычитания и сдвигов. Поскольку вычитание заменяется сложением чисел в обратном или дополнительном коде, то можно сказать, что деление — это последовательность операций сложения и сдвигов. Знак частного получается аналогично знаку произведения. При делении двоичных чисел с фиксированной запятой частное необходимо анализировать на переполнение разрядной сетки, поскольку в процессе вычислений может возникнуть вариант, когда делимое больше делителя.

Деление двоичных чисел сводится к операциям умножения и вычитания.

Деление двоичных чисел выполняется аналогично делению десятичных чисел, но при делении двоичных чисел используются двоичные таблицы умножения и вычитания.

Деление двоичных чисел производится аналогично делению десятичных чисел, но с учетом специфики операции вычитания двоичных чисел. Положение запятой результата умножения и деления определяется так же, как и для десятичных чисел.

Деление двоичных чисел выполняется так же, как и десятичных.

Деление двоичных чисел также обычно. Как и для десятичных чисел, здесь возможно деление с остатком. Остаток и частное от деления также представляют собой двоичные числа.

Деление двоичных чисел производят по следующим правилам: 1: 1 1 0: 10, а деление на 0 вообще недопустимо.

Деление двоичных чисел происходит с использованием двоичных таблиц умножения и вычитания.

Рассмотрим деление двоичных чисел по методу с восстановлением остатка. Деление осуществляется последовательным повторением циклов.

Операция деления двоичных чисел с фиксированной запятой сводится в ЭВМ к последовательности действий вычитания делителя сначала из делимого, а затем из частичных остатков, образующихся в ходе вычислений, и последующего сдвига частичных остатков на один разряд влево. Деление в ЭВМ может выполняться двумя различными методами: с восстановлением и без восстановления остатка. В методе с восстановлением остатка при этом выполняется следующее: к отрицательному остатку прибавляется делитель, чтобы восстановить (отсюда и название метода) предыдущий частичный остаток, и полученный результат сдвигается на 1 разряд влево. Однако в современных ЭВМ метод деления с восстановлением остатка встречается редко, поэтому более подробно рассмотрим алгоритм деления без восстановления остатка. Сущность метода состоит в следующем. На каждом шаге вычислений перед очередным нахождением разности частичный остаток сдвигается на 1 разряд влево и далее проводится анализ остатка.

ДЕЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ

Если умножение выполняется путем многократных сдвигов и сложений, то деление, будучи операцией обратной умножению,- путем многократных сдвигов и вычитаний.

(ПРАВИЛЬНЫЕ ДРОБИ, БЕЗ ЦЕЛОГО.)

Рассмотрим сначала пример деления «ручным» способом.

В машинах вместо сдвига делителя вправо осуществляется сдвиг остатка влево, что, по сути, ничего не изменяет.

Посмотрим, как решается предыдущий пример на машине.

1) Определить знак частного суммированием по модулю два содержимых знаковых разрядов делимого и делителя.

3) Запомнить знак остатка.

4) Сдвинуть остаток на один разряд влево.

5) Присвоить делителю знак, обратный знаку остатка, запомненному в п. 2.

6) Сложить сдвинутый остаток и делитель (с учетом знака).

7) Присвоить цифре частного значение, противоположное коду знака остатка.

8) Повторять выполнение пунктов 3-7 до тех пор, пока не будет обеспечена требуемая точность вычисления частного.

Решение рассмотренного выше примера в данном случае осуществляется по следующей схеме:

С ПЛАВАЮЩЕЙ ЗАПЯТОЙ

Деление выполняется в следующей последовательности.

3) Полученный в последнем цикле деления остаток Rs+1, если он положительный, сдвигается вправо на S разрядов; если же Rs+1 0, а Q- 0)
Если же -1 < G+ + Q- < 0, то (G+ + Q-) + 2 < 2 и переноса из разряда знака не возникает. В этом случае:
(G+) пр + (Q-) доп = (G+ + Q-) доп
(G+ + Q- < 0).
Применение дополнительного или обратного кода для представления отрицательных чисел упрощает операцию алгебраического сложения. Алгебраическое сложение чисел с разными знаками заменяется арифметическим сложением кодов, при этом автоматически получается код знака результата. Однако остается нерешенным вопрос о выработке признака переполнения разрядной сетки.
При сложении кодов теряется единица переноса из разряда целых единиц и результат ошибочно воспринимается как положительное число, меньшее единицы.
Отметим, что при алгебраическом сложении двух чисел G и Q, каждое из которых по модулю меньше единицы, может возникнуть переполнение разрядной сетки, но при этом модуль получаемой суммы всегда меньше двух. Это обстоятельство облегчает построение кодов, по виду которых можно судить о переполнении разрядной сетки.
Для получения признака переполнения разрядной сетки применяют модифицированные прямой, дополнительный и обратный коды. Эти коды отличаются от ранее рассмотренных кодов тем, что для представления знака используются два разряда.
При этом знак плюс обозначается 00, а знак минус — 11. При алгебраическом сложении чисел знаковые разряды рассматриваются как разряды целой части числа.
При возникновении переноса единицы из старшего разряда знака эта единица отбрасывается, если отрицательные числа представляются модифицированным дополнительным кодом, или производится циклический перенос в младший разряд мантиссы, если отрицательные числа изображаются модифицированным обратным кодом.
При алгебраическом сложении на переполнение разрядной сетки (модуль алгебраической суммы больше единицы) указывает несовпадение цифр в знаковых разрядах. Комбинации 01 в знаковых разрядах соответствует положительное число, а комбинации 10 — отрицательное число.
В этих случаях модуль суммы:
1 ≤ |x| < 2
Отметим также особенности нормализации и выполнения сдвига для отрицательных чисел, представленных в дополнительном (обратном) коде.
У нормализованного положительного или отрицательного числа с мантиссой, изображаемой в прямом коде, цифра в старшем S-ичном разряде мантиссы должна быть отлична от нуля. Для отрицательных мантисс, представленных в обратном или дополнительном коде, условие нормализации |q| ≥ 1/Sвыполняется, если цифра в старшем S-ичном разряде мантиссы есть нуль.
В случае чисел с плавающей запятой комбинации 01 и 10 в знаковых разрядах мантиссы указывают на нарушение нормализации влево, а комбинации цифр 00 и 1 σs1 (σs1 ≠ 0) в младшем знаковом разряде и старшем S-ичном цифровом разряде мантиссы сигнализируют о нарушении нормализации вправо. Для восстановления нормализации производится сдвиг мантиссы вправо (или влево) на нужное число разрядов, при этом порядок увеличивается (уменьшается) на соответствующее число единиц,
Если отрицательные числа представляются в дополнительном (обратном) коде, сдвиг производится по особым правилам («модифицированный сдвиг»), с тем чтобы в результате сдвига дополнительного (обратного) кода числа х на m S-ичных разрядов получился дополнительный (обратный) код числа Smx или S-mх соответственно для сдвига влево или вправо.
При модифицированном сдвиге дополнительного (обратного) кода вправо в освобождающиеся старшие разряды мантиссы записываются единицы, а при сдвиге влево единицы записываются в освобождающиеся младшие разряды.
Деление в прямом, обратном и дополнительном кодах
Деление в вычислительной машине обычно сводится к выполнению последовательности вычитаний делителя сначала из делимого, а затем из образующихся в процессе деления частичных остатков и сдвига частичных остатков на один разряд влево.
Необходимо отметить, что в машинах, оперирующих над числами с запятой, фиксированной перед старшим разрядом, деление возможно только в одном случае, если делимое по модулю меньше делителя. В противном случае частное превышает единицу и выходит за пределы разрядной сетки числа. Если в результате вычитания выясняется, что делимое или очередной частичный остаток больше или равны делителю, то в очередной разряд частного записывается единица и полученный в результате вычитания частичный остаток сдвигается влево на один разряд. Если в результате вычитания выясняется, что делимое или очередной частичный остаток меньше делителя, то в очередной разряд частного записывается нуль, к полученной разрядности добавляется делитель, чтобы восстановить предыдущий частичный остаток, и результат сдвигается влево на один разряд. Метод выполнения деления, когда в случае получения отрицательного остатка при вычитании (частичный остаток меньше делимого) к нему прибавляется делитель, называется методом деления с восстановлением остатка.
Рассмотрим пример деления с восстановлением остатка (см. таблицу). Для выполнения операции вычитания будем использовать дополнительный код. Деление с восстановлением остатка требует в наиболее неблагоприятном случае трёх тактов для формирования одного разряда частного: такта вычитания, такта сложения и такта сдвига.
Рассмотренный метод носит название деления с восстановлением остатка .
Недостатком этого метода является необходимость введения специального третьего такта для восстановления остатка, который значительно замедляет ход вычисления.
Обычно в вычислительных машинах для деления широко используется другой метод, называемый методом выполнения деления без восстановления остатка . Этот метод основан на прямом копировании действий при ручном делении («в столбик»).
При этом методе, если результат вычитания получился отрицательный, частичный остаток не восстанавливается путём прибавления делителя, а на следующем шаге деления вместо вычитания делимого производится его прибавление к частичному остатку. Если результат при этом остался отрицательным, то в очередную цифру частного записывается нуль и на следующем шаге также выполняется сложение. Если результат сложения получился положительным, то в очередной разряд частного записывается единица и на следующем шаге производится вычитание.
Можно показать, что частичные остатки при делении без восстановления остатка получаются такими же, как и остатки после сдвига восстановленного остатка при делении с восстановлением остатка.
Действительно, поскольку сдвиг частичного остатка на один разряд влево эквивалентен умножению его на два, получим:
2a – b = 2(a –b) + b
где a – частичный остаток; b – делитель.
Аналогично:

Деление без восстановления остатка всегда требует для получения одной цифры частного только двух тактов: такта сложения или вычитания и такта сдвига. Тем самым скорость вычисления этим методом оказывается выше чем в методе деления с восстановлением остатка.
Деление правильных дробей выполняется также, как деление целых чисел. Разница же заключается в том, что делимое имеет, как правило, такую же длину, как и делитель. Однако можно предположить, что делимое имеет ещё n младших разрядов, равных 0. Тогда становится ясно, что алгоритм деления дробей ничем не отличается от алгоритма деления целых чисел.
Исходя из рассмотренных методов деления в вычислительных машинах наиболее скоростной и простой метод является метод деления без восстановления остатка, так как при использовании данного метода для получения одной цифры частного необходимо выполнить всего лишь два такта, в то время как в методе с восстановлением частичного остатка для получения одной цифры частного требуется три такта.

Заключение
В данной курсовой работе были рассмотрены различные системы счисления (двоичная, восьмеричная, шестнадцатеричная), элементы двоичной «арифметики» а также реализация способов двоичной арифметики в цифровых вычислительных системах.
В частности были рассмотрены методы двоичного сложения (алгебраического сложения), умножения и деления. Метод двоичного деления был рассмотрен более близко.
Мы рассмотрели два основных метода реализации двоичного деления в цифровых вычислительных системах. Напрашивается вывод:
после глубокого рассмотрения двух методов реализации двоичного деления выяснилось, что метод с восстановлением частичного остатка является трудоёмким и неудобным, а также оказывается очень медленным в силу того, что для нахождения одного числа частного в этом методе требуется совершить три такта (такт вычитания, такт сложения и такт сдвига), в то время когда в методе без восстановления частичного остатка требуется всего лишь два такта (такт сложения(вычитания) и такт сдвига).
Становится ясно, что более эффективным и простым методом для деления двоичных чисел является метод без восстановления частичного остатка, основанный на делении двоичных чисел в прямом, обратном и дополнительном кодах.
Работа журналиста в прямом эфире на примере программ Город сегодня и

Источник