- Чтение математических выражений учебно-методический материал по математике (1, 2 класс) на тему
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Числовые и буквенные выражения
- Числовые выражения
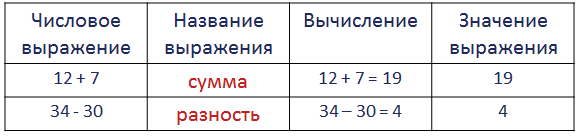
- Чтение числовых выражений
- Решение числовых выражений
- Сравнение значений числовых выражений
- Буквенные выражения
- Алгоритм решения буквенного выражения
- Переменные
- Речевое развитие младших школьников на уроках математики статья по математике на тему
- Скачать:
- Предварительный просмотр:
Чтение математических выражений
учебно-методический материал по математике (1, 2 класс) на тему
Памятка «Чтение математических выражений» во 2 классе
Скачать:
| Вложение | Размер |
|---|---|
| Памятка «Чтение математических выражений» во 2 классе | 14.95 КБ |
Предварительный просмотр:
5- первое слагаемое
2 – второе слагаемое
Чтобы найти первое слагаемое, надо из суммы вычесть второе слагаемое.
Чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое.
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое , надо из уменьшаемого вычесть вычитаемое
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
5-= первое слагаемое
2 – второе слагаемое
Чтобы найти первое слагаемое, надо из суммы вычесть второе слагаемое.
Чтобы найти второе слагаемое, надо из суммы вычесть первое слагаемое.
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое , надо из уменьшаемого вычесть вычитаемое
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
— к десяти прибавить разность чисел пяти и двух
— десять увеличить на разность чисел пяти и двух
— первое слагаемое 10, второе представлено разностью чисел пяти и двух
— из десяти отнять сумму чисел пяти и двух
— десять уменьшить на сумму чисел пяти и двух
— уменьшаемое 10, вычитаемое представлено суммой чисел пяти и двух
По теме: методические разработки, презентации и конспекты
Урок математики «Математические выражения».3 класc. Образовательная программа «Начальная школа XXIвека»
Урок математики в 3 классе. Тема урока : «Математические выражения». Закрепление умений читать выражения разными способами, устанавливать порядок действий, находить значения выражений, составлят.
Урок математики в 4 классе по теме «Решение математических выражений, уравнений».
Данный урок включает в себя нестандартный подход к решению математических выражений, учит сравнивать и анализировать разные типы уравнений.
Урок математики в 4 классе по теме «Решение математических выражений, уравнений».
Данный урок предполагает нестандартный подход к решению математических выражений.
Конспект урока математики в 3 классе по теме «Решение математических выражений на порядок действий.»
Конспект урока математики в 3 классе по теме «Решение математических выражений на порядок действий.» Цели: 1. Совершенствовать вычислительные навыки выполнения арифметичес.
Методическая разработка урока математики в 1 классе по теме «Составление математических выражений и их сравнение.».
По данной презентацииможно построить урок в 1 классе.
Проверочная работа по математике 1 класс 4 четверть. Контроль формирования навыков решения задач, математических выражений в одно и два действия, неравенств.
Проверочная работа по математике 1 класс 4 четверть направлена на проверку навыков решения задач, математических выражений в одно и два действия. При решении неравенств дети применяют знан.
Конспект урока «Всегда ли математическое выражение является числовым?» (4 класс, УМК «Перспективная начальная школа»)
Цель: познакомить с новым типом математического выражения — буквенным.Планируемые результаты:Личностные:Формировать интерес к познанию, к новому учебному материалу, к овладению новыми способами .
Источник
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения — это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения — это 76.
Чтение числовых выражений
49 — 20 — разность
34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21
13 + (26 — 8) — к 13 прибавить разность чисел 26 и 8
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 — 6 и 18 — 9.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением .
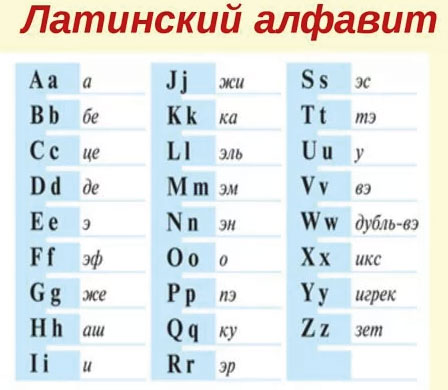
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм — значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Источник
Речевое развитие младших школьников на уроках математики
статья по математике на тему
Скачать:
| Вложение | Размер |
|---|---|
| rechevoe_razvitie_mladshih_shkolnikov_na_urokah_matematiki.doc | 978.5 КБ |
Предварительный просмотр:
Речевое развитие младших школьников на уроках
Учитель первой квалификационной категории
МОУ «Дедловская ООШ»
Медведева Елена Витальевна
Важнейшей задачей школы на современном этапе является формирование у учащихся потребности к овладению знаниями и способами действий с ними в соответствии с познавательными установками.
В современных условиях, когда объем необходимых человеку и обществу знаний быстро возрастает, уже нельзя ограничиваться лишь освоением определенного количества знаний: важно развить у учащихся потребность и умение постоянно пополнять свои знания и умения, ориентироваться в стремительном потоке информации. Одно из решающих условий этой задачи – хорошо развитая речь каждого человека общества. Поскольку средством обучения и источником необходимой информации, прежде всего, является речь, то основной перечень общеучебных умений непосредственно соотноситься с формированием у учащихся навыков речи.
Большинство детей к моменту обучения в школе уже полностью овладевают звуковой стороной речи, имеют довольно развёрнутый словарный запас, умеют грамматически правильно строить предложения. Однако не у всех процесс овладения речью происходит одинаково. В ряде случаев он может быть замедленным, и тогда у детей отмечаются различные отклонения, нарушающие нормальный ход речевого развития. Наибольшие трудности у детей вызывают задания, требующие непосредственного участия речи при их выполнении. Наблюдаются трудности программирования речевого высказывания и недостаточность его грамматического оформления. Всё это снижает познавательную активность, тормозит процесс приобретения математических знаний.
Подводя итоги выше сказанного можно сделать вывод, что речь является основным средством обучения и источником необходимой информации. Логическая, чёткая, документальная, образная речь учащихся является одной из главных задач обучения. Чем активнее обучаемые совершенствуют свою речь, пополняют свой словарный запас, тем выше их уровень познавательных возможностей и культуры.
Учебный процесс подразумевает развитие речи на всех уроках, в том числе и на уроках математики. Но математический язык кардинально отличается от естественного языка. При изучении математики особую важность играет умение логически мыслить и правильно рассуждать. Таким образом, речевая деятельность учителя должна носить информационно познавательный, коммуникативный, стимулирующий характер, постоянно и целенаправленно способствовать речевому развитию младшего школьника.
Для организации работы по развитию речи можно использовать упражнения из учебника по математике любой программы.
Особенностью работы является то, что учитель специально не подбирает дополнительные упражнения, а использует содержание учебника.
Задания изменены таким образом, что цель задания сохранена, но его вид или формулировка направлены на максимальное участие речи детей при выполнении данного задания.
Все предлагаемые упражнения можно дифференцировать по следующим темам:
- Работа с числовыми выражениями.
- Работа с условием задачи.
- Работа с геометрическим материалом (исходя из требований программы).
Работа с числовыми выражениями.
Работа с числовыми выражениями, ведётся по 2 направлениям:
1 направление : Чтение числовых выражений разными способами. При этом использовались разные формы работы:
- чтение числовых выражений учащимися выбранным ими способом
- чтение числовых выражений учащимися способом, который предлагает учитель, бросая ребятам мяч (игровая форма снизит нежелание детей читать выражения способом, который труден для того или иного ученика)
- чтение числовых выражений учащимися способом, который они вытащили из сюрпризного конверта и т.д.
У каждого из учеников на парте лежит конверт. В конверте написан способ или способы чтения данных числовых выражений.
- чтение числовых выражений учащимися всеми перечисленными способами
2 направление : Соотнесение словесной записи числовых выражений и знаковой.
Задания могут быть разной степени сложности:
- Одной знаковой записи будет соответствовать 1 словесная запись.
- Одной знаковой записи будут соответствовать 2-3 словесные записи.
- Знаковой записи не будет соответствовать словесная запись.
- Исправление ошибок в словесной записи числовых выражений.
- Самостоятельная запись словесной формулировки числовых выражений.
Работе с числовыми выражениями необходимо уделять особое внимание. Чтение числовых выражений разными способами способствует более интенсивному развитию звуковой стороны речи и обогащению словарного запаса учащихся; формированию правильного произношения и употребления математических терминов (их понимание и умение объяснить значение этих терминов); формированию умения составлять связное высказывание, а также усвоению правильного написания математических терминов при работе по соотнесению словесной записи числовых выражений и знаковой.
Рассмотрим примеры основных видов заданий, которые были использованы нами в процессе обучения.
1. Прочитайте выражения разными способами, используя образец на доске с ключевыми словами.
- минус
- из … вычесть ….
- плюс
- к… прибавить…
При выполнении учащимися данного задания выражения могут быть прочитаны например, таким образом:
- девятнадцать минус тринадцать
- из девятнадцати вычесть тринадцать
Так как в этом задании числовых выражений выбранных для чтения немного, то каждое числовое выражение может быть прочитано 2 способами.
2. Соотнесение словесной записи числовых выражений и знаковой и
Источник