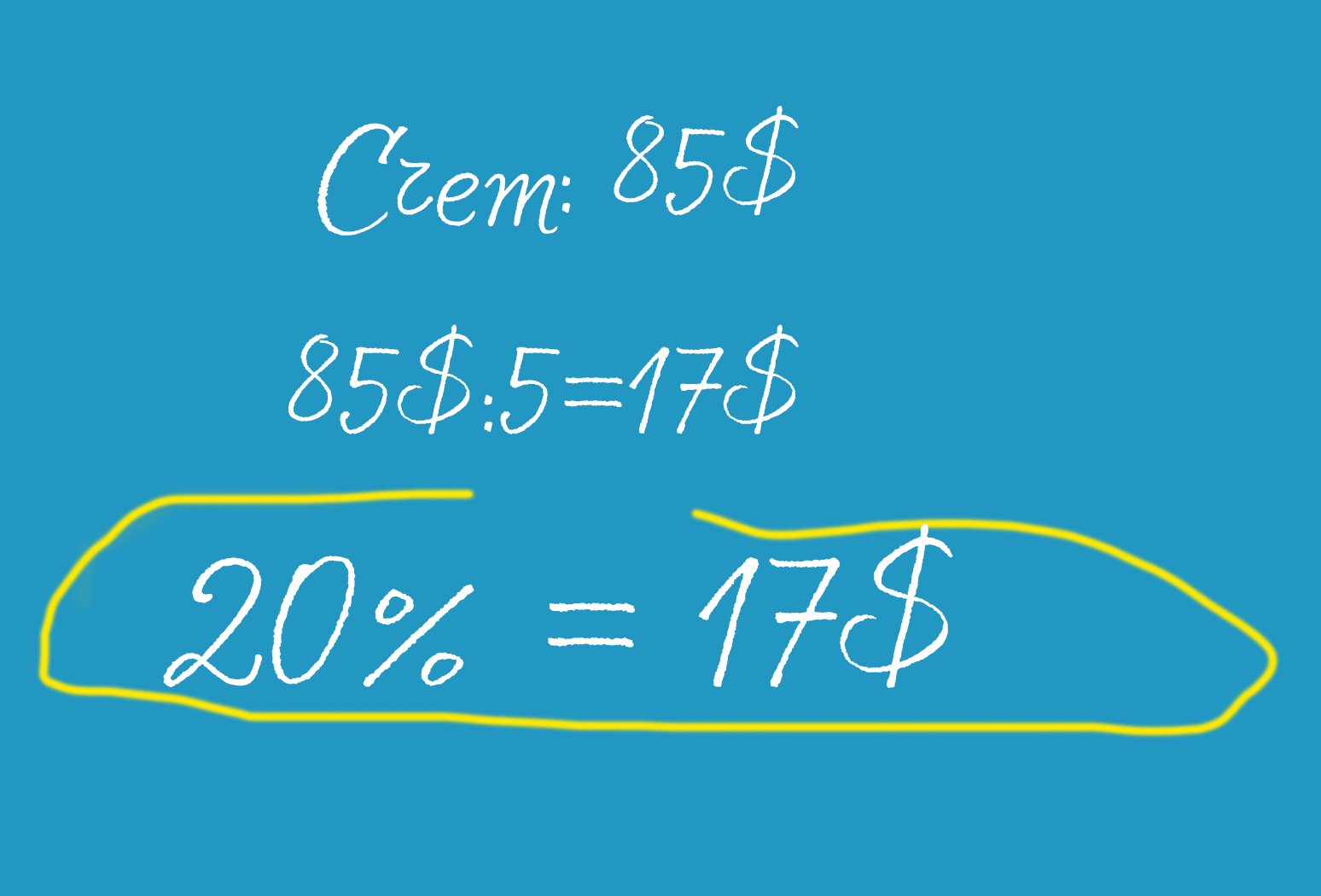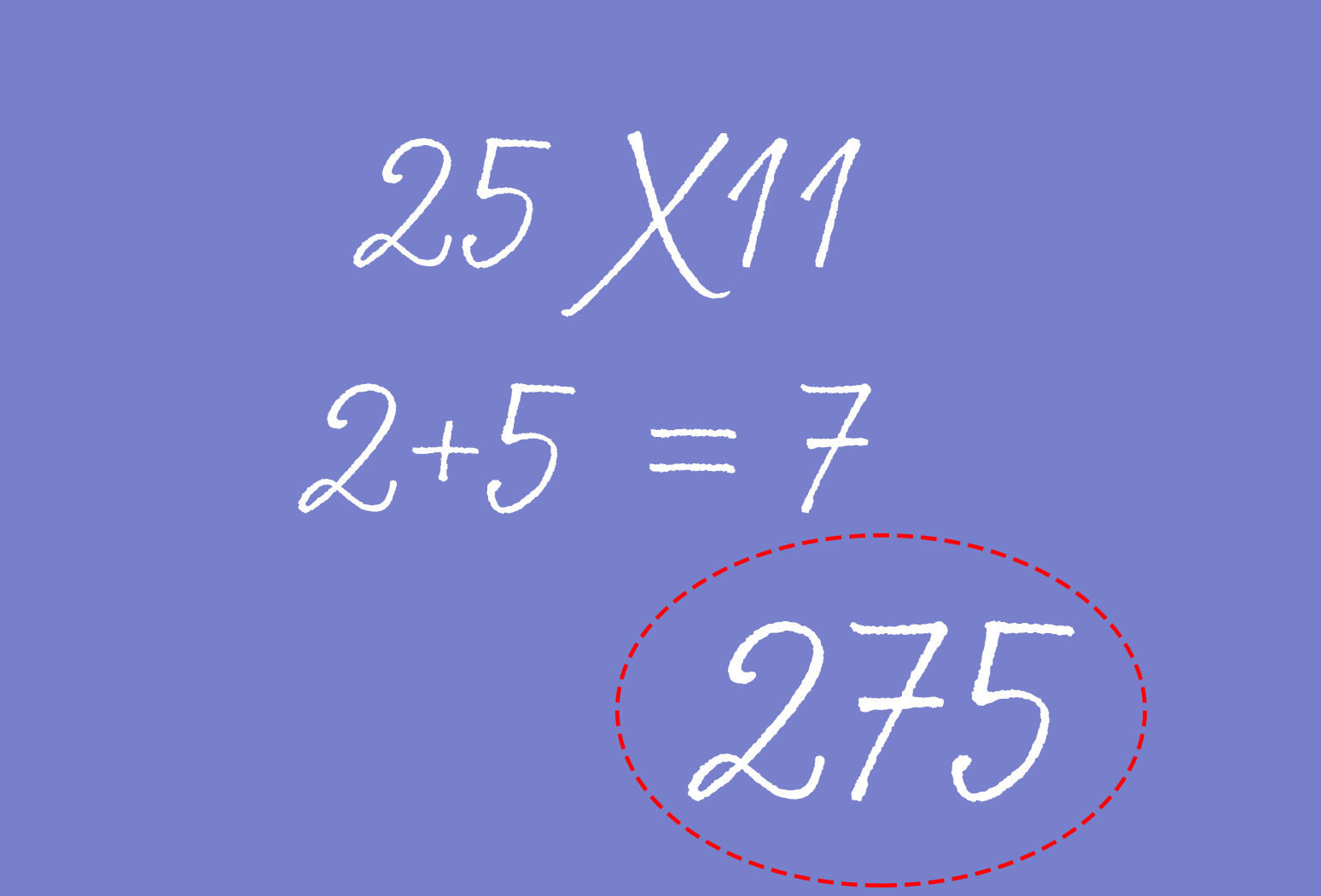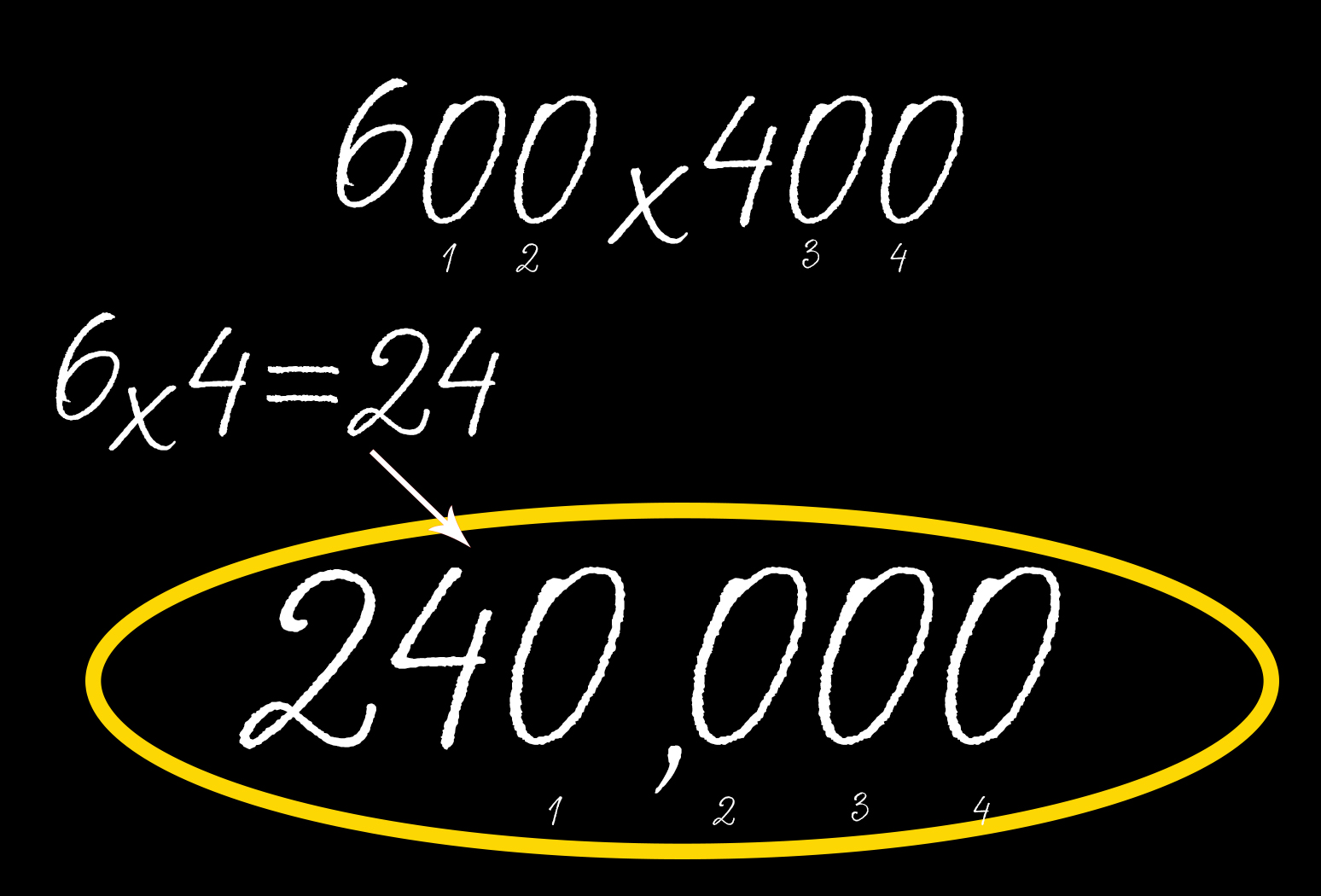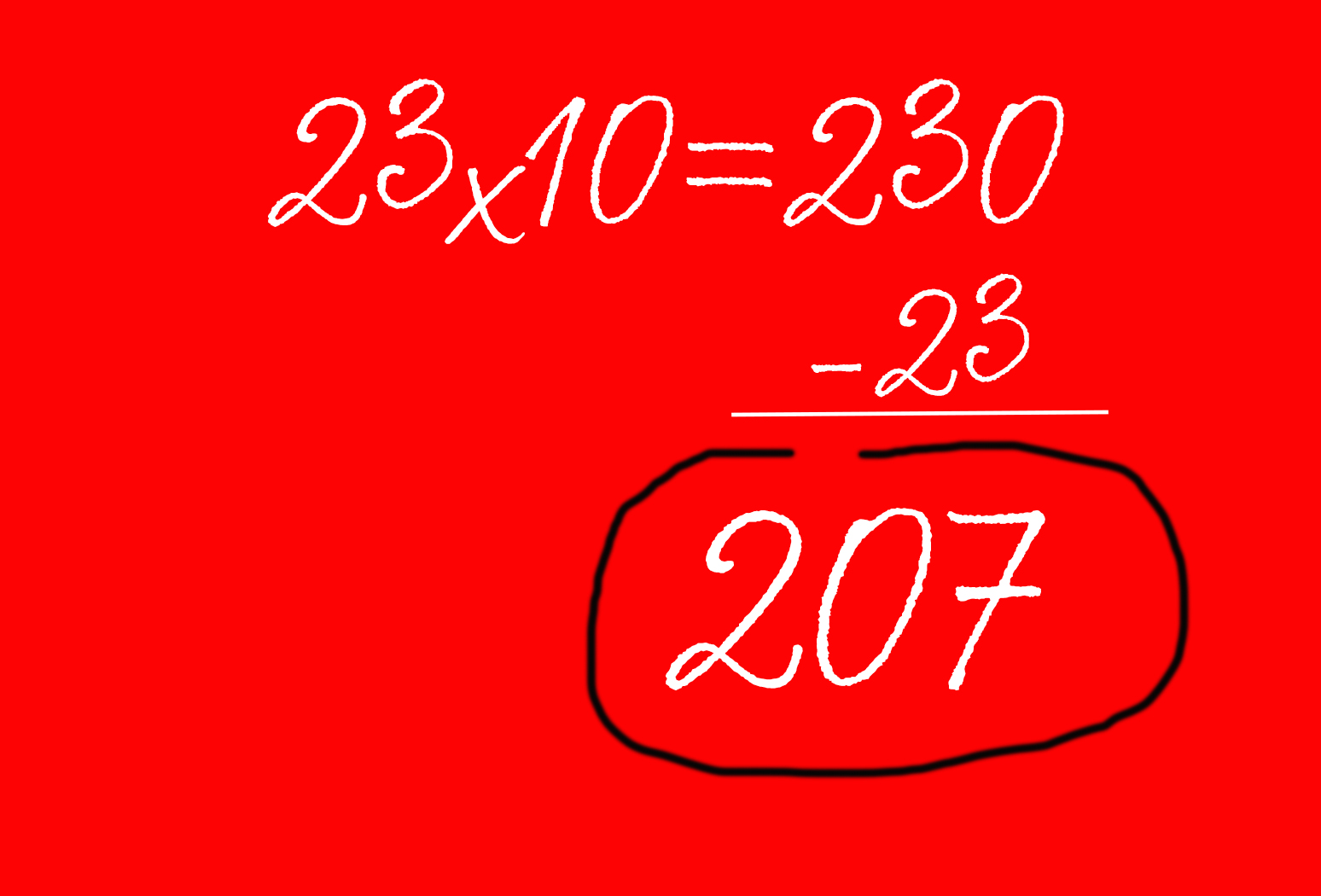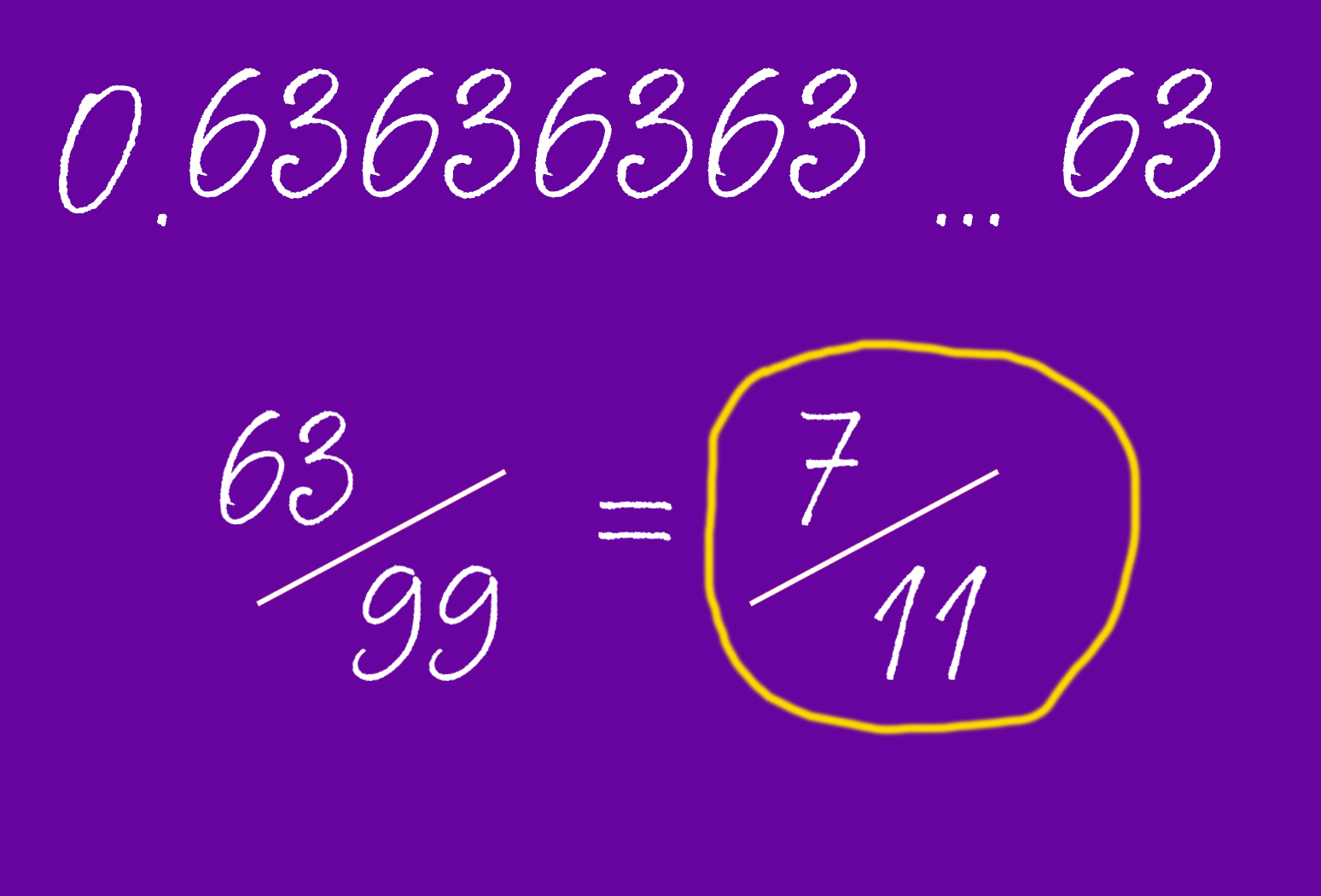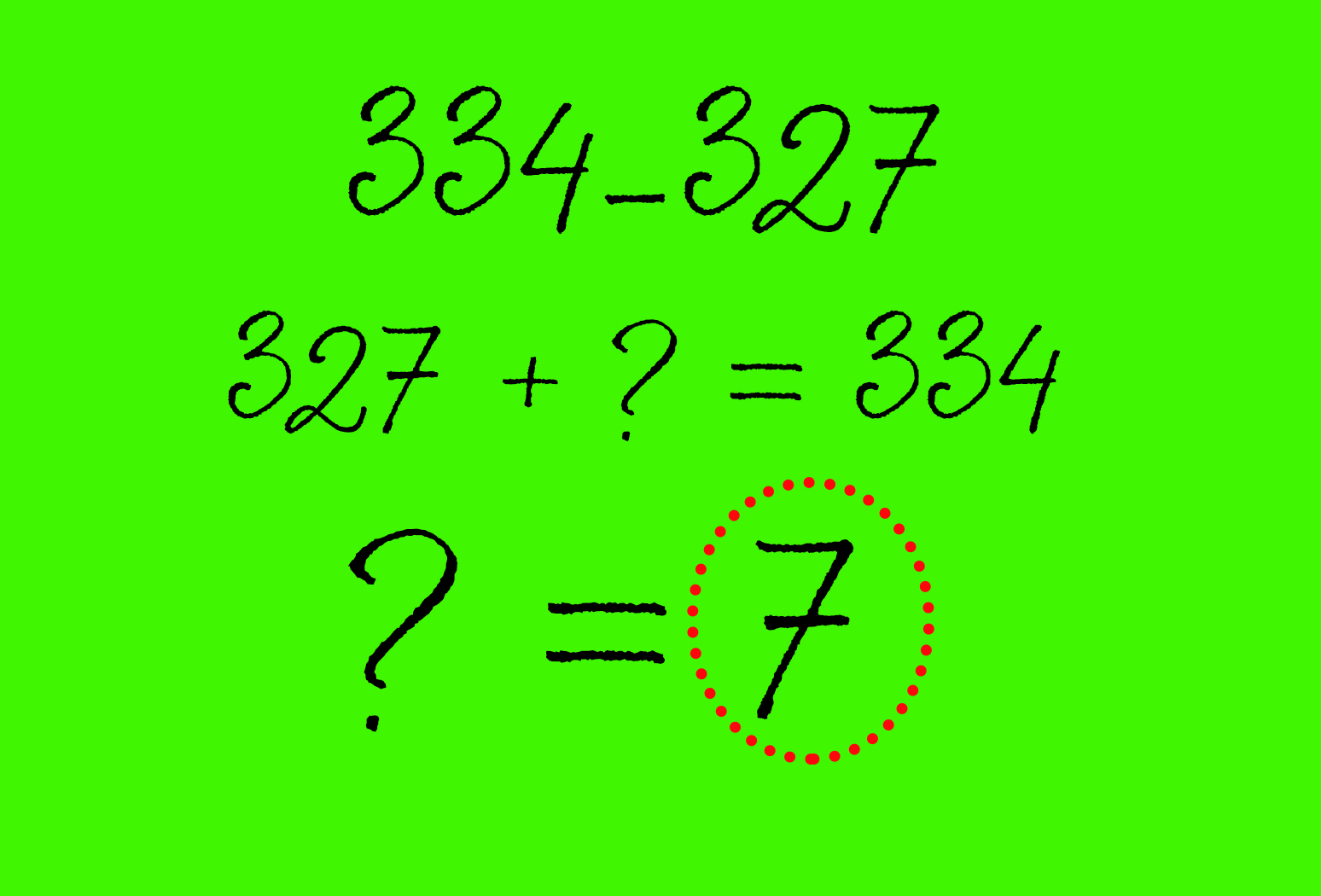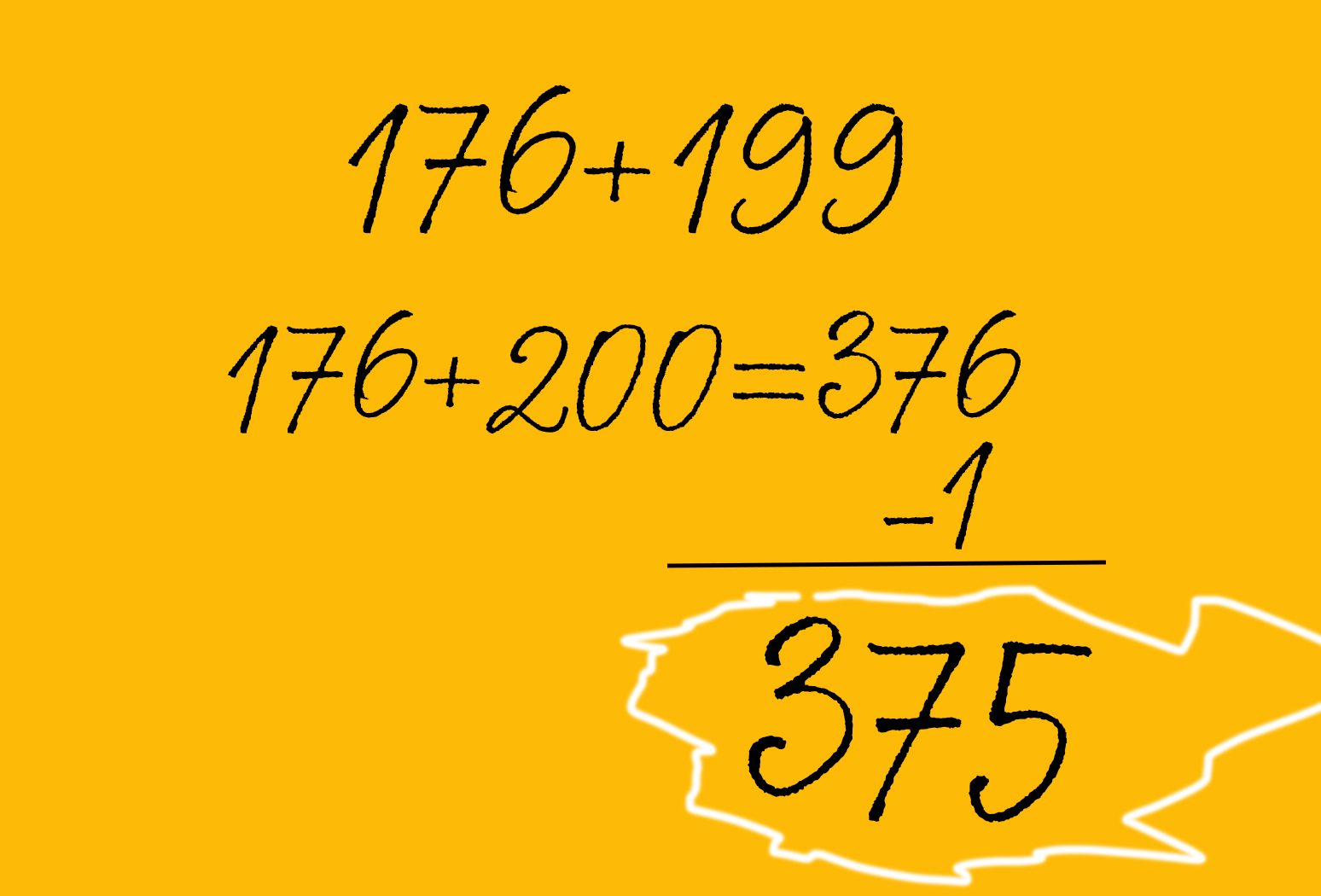Способы быстрого вычисления по математике

Способы быстрого вычисления по математике

Математическое обоснование:
Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b

Умножение и деление на 5 и 25
Чтобы число умножить число на 5, его нужно разделить на 2 и умножить на 10. Чтобы число разделить на 5, его нужно умножить на 2 и разделить на 10.
Аналогично, умножение/деление на 25 заменяется делением/умножением на 4 и умножением/делением на 100

3/5
Умножаем 3 на 2 и получаем 6. Делим 6 на 10 и получаем 0,6

45/25
Умножаем 45 на 4, получаем 180. Делим 180 на 100, получаем 1,8

84х25
Делим 84 на 4, получаем 21. Умножаем 21 на 100 и получаем 2100.

Математическое обоснование:
Поскольку 5=10/2, умножение/деление на 2 можно свести к более простым умножениям/делениям на 2 и 10

Возведение в квадрат числа, оканчивающегося на 5

Чтобы возвести в квадрат число, оканчивающееся пятёркой, нужно умножить число, полученное отбрасыванием последней пятёрки на следующее в натуральном ряду, и к результату приписать 25.

Примеры:
652
Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.

1152
Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.

Математическое обоснование:
Возведём в квадрат число 10n+5. (10n+5)2 = 100n2+100n+25 = 100n(n+1)+25, откуда и следует данное правило.

Возведение в квадрат числа, близкого к круглому

Целесообразно воспользоваться формулами квадрата суммы или разности.

Примеры:
192 = (20-1)2 = 400–40+1=361

422 = (40+2)2 = 1600+160+4 = 1764

Математическое обоснование:
Формула квадрата суммы: (a+b)2 = a2+2ab+b2
Формула квадрата разности: (a-b)2 = a2–2ab+b2

Вычитание из степени десятки

Для вычитания числа из степени десятки, нужно последнюю его цифру заменить дополнением до десяти, а остальные (включая первые виртуальные нули) – дополнениями до девяти.

Примеры:
1000-725 = (9-7)(9-2)(10-5) = 275
100000 – 1237 = 100000 – 01237 = (9-0)(9-1)(9-2)(9-3)(10-7) = 98763

Математическое обоснование:
Правило следует из алгоритма вычитания столбиком.

Прибавление числа, близкого к степени десятки

Вместо прибавления числа, состоящего из девяток и оканчивающегося на 9 (8, 7, 6 и т.д.), прибавьте следующую большую степень десятки и вычтите 1 (2, 3, 4 и.т.д)

Примеры:
125+999 = 1125-1 = 1124
6528+996 =7258-4=7254

Математическое обоснование:
Для k-значного числа 99…9 = 100..00 – 1

Упрощённые признаки делимости на 4 и 8
Обычно для проверки делимости на 4 применяется следующий признак: Если двуциферное окончание числа делится на 4, то и само число делится на 4.
Однако, использовав обобщённый признак делимости, заметим, что число 10 даёт остаток 2 при делении на 4. Поэтому переформулируем правило так: Если сумма последней цифры с удвоенной предпоследней делится на 4, то и само число делится на 4.
Аналогично для делимости на 8. Вместо проверки на делимость трёхциферного окончания, можно выполнять проверку суммы последней, удвоенной предпоследней и учетверённой третьей с конца цифры.

Примеры:
Число 1324
4+2*2=8 – делится на 4.
4+2*2+3*4=20 – не делится на 8

Источник

Долой калькулятор: 12 простых трюков, которые помогут вам быстро считать

Просто, как дважды два.

Как бы мы ни хотели это признавать, учителя были правы: математика нужна каждому из нас. Но далеко не всем дается ловкое жонглирование числами. Тогда на помощь приходят легко запоминающиеся математические приемы – настоящее спасение, когда под рукой, как назло, нет калькулятора.

Ниже вы найдете 12 способов быстрых вычислений для всех, кто далек от точных наук.

1. Быстрое вычисление 20%

Представим, что границы вновь открыли и первым делом вы отправились в США. А там принято оставлять на чай. Обычно размер чаевых составляет 15-20% от суммы вашего заказа.

По словам Кейт Сноу, автора серии книг The Math Facts That Stick, чтобы быстро вычислить 20% от суммы, вам нужно просто разделить число в чеке на 5.

Например, вы поели на 85 долларов. Разделите 85 на 5, и у вас получится 17 долларов – чаевые, которые вы должны оставить официанту.

2. Умножение двузначных чисел на 11

Умножить число на 11 очень легко с помощью хитрого трюка от math.hmc.edu. Просто сложите две цифры и поместите полученную сумму в середину числа.

Например, вы умножаете 25 на 11. Если сложить 2 и 5, получится 7. Теперь расположите 7 между 2 и 5, чтобы найти окончательный ответ – 275.

3. Быстрое удвоение

Чтобы удвоить большое число, умножьте каждую цифру на 2 и сложите их между собой. Кейт Сноу предлагает начинать слева – так будет легче.

«Чтобы удвоить, к примеру, 147, начните с разряда сотен. Если умножить 100 на 2, получится 200. 40 на 2 – 80. 7 на 2 – 14. Теперь сложите числа между собой (200 + 80 + 14), и вы получите 294», – объясняет Сноу.

4. Умножение чисел, которые оканчиваются на ноль

Примеры с большими пугающими числами, которые оканчиваются на ноль, тоже легко решить с помощью специального приема. Согласно education.cu-portland.edu, нужно просто «вычеркнуть» нули из примера, а в конце вновь их добавить.

Если вы умножаете 600 на 400, уберите все нули и перемножьте 6 на 4. Получится 24. Затем подсчитайте общее количество нулей в исходном уравнении и припишите их к полученному значению. Так как в нашем примере было четыре нуля, то ответ будет равен 240000.

5. Умножение на 9

Если вам так и не удалось выучить таблицу умножения – не переживайте. По словам Сноу, чтобы легко умножить число на 9, нужно умножить его на 10 и вычесть исходное число из полученного значения.

Например, вам нужно умножить 9 на 23. Для этого умножаем 23 на 10 и получаем 230. А затем вычитаем из него 23, чтобы получить окончательный ответ – 207.

6. Деление на 10, 100 или 1000

Разделить число на 10 проще простого – согласно Сноу, «нужно просто переместить десятичный знак на одну позицию влево от исходного числа, чтобы найти ответ».

Для деления на 100 применим тот же метод, за исключением одного – нужно переместить десятичный разряд на две позиции левее исходного числа. Что касается деления на 1000, просто переместите десятичный знак на три позиции влево.

Например, если вы делите 42,94 на 10, вы просто перемещаете десятичный знак на одну позицию влево и получаете 4,294.

7. Умножение на 10, 100 или 1000

Здесь все работает с точностью до наоборот. Чтобы умножить число на 10, переместите десятичный знак на одну позицию вправо. На 100 – на две позиции. На 1000 – на три позиции.

Например, если вам нужно умножить 366,78 на 100, передвиньте десятичный знак на две цифры вправо, чтобы получить ответ 36678.

8. Преобразование периодической десятичной дроби в обыкновенную

Согласно businessinsider.com, нужно выполнить всего 3 шага, чтобы легко превратить бесконечную десятичную дробь в обыкновенную, с числителем и знаменателем.

• Шаг 1. Найдите повторяющиеся цифру или число. Например, у 0,636363 это будет 63.
• Шаг 2. Определите, сколько разрядов в этом числе. В нашем случае у 63 – два разряда.
• Шаг 3. Разделите повторяющееся число на число с таким же количеством разрядов, которое будет состоять из одних девяток – в данном случае 99. Получим 63/99. Теперь сократим ее и получим 7/11 – наш ответ.

9. Умножение на 25

Умножать на 25 не так уж и сложно, если представлять число в виде дроби 100/4. В этом случае все, что вам нужно сделать, это разделить число на 4 и умножить на 100.

Например, вам нужно умножить 84 на 25. Сначала делим 84 на 4 – получаем 21, а потом умножаем значение выражения на 100. Ответ: 2100.

10. Возведение чисел, оканчивающихся на 5, в квадрат

«Этот математический трюк подразумевает 2 шага», – объясняет Сноу. Чтобы возвести в квадрат число, которое оканчивается на пять, возьмите первую цифру числа и умножьте ее на себя. После этого прибавьте к полученному результату первую цифру и припишите к ответу 25. Кружится голова? Разберем на примере.

Если вы умножаете 35 на 35, сначала умножьте 3 на 3 – получится 9, – и прибавьте 3 к ответу – получится 12. Теперь припишите 25 в конец найденного числа, и вы найдете окончательный ответ: 1225.

11. Вычитание путем сложения

Если вам кажется, что сложение немного проще, чем вычитание, этот трюк для вас. Когда вам нужно найти разность двух чисел, достаточно близких друг к другу, попробуйте решить пример с помощью сложения.

«Вместо того чтобы пытаться вычесть 327 из 334, представьте это в виде суммы: мол, сколько нужно добавить к 327, чтобы получить 334?» – объясняет Сноу.

12. Сложение чисел, оканчивающихся на 99

Если вы пытаетесь прикинуть, во сколько обойдутся продукты, стоимость которых заканчивается на 99, – калькулятор не нужен. Все, что необходимо сделать, – прибавить 100 вместо 99, а потом вычесть единицу.

Сноу объясняет этот процесс на примере 176 + 199 = 375. «Если к 176 мы прибавим 200, то получим 376, – говорит эксперт. – Поскольку вы добавили на единицу больше, чем вам нужно, вычтите ее из 376, чтобы найти правильный ответ: 375».

Источник

Приемы быстрых вычислений

«Лучше усваиваются те знания,

которые поглощаются с аппетитом»

Анатоль Франс, французский писатель

Приемы быстрых вычислений

В самом обыкновенном устном счете, как и во многом другом, можно видеть много интересного, необычного и чудесного.

Математика – это инструмент для изучения других наук и различных сфер жизни, это не просто «сухие» цифры, формулы, а как сказал Аристотель: «Математика… выявляет порядок, симметрию, определенность, а это – важнейшие виды прекрасного».

Вряд ли кто-нибудь будет оспаривать необходимость вычислительной культуры современного человека.

Не потеряли своей актуальности слова М.В. Ломоносова о том, что арифметику за тем уже изучать стоит, что она ум в порядок приводит.

С приходом в нашу жизнь и школу калькуляторов, современные школьники перестали использовать устные формы вычислений. Между тем устный счет в их развитии нельзя заменить никакими калькуляторами.

Необходимо находить время на уроках для знакомства с приемами устного счета, тогда школьники не будут пользоваться калькуляторами.

В предлагаемой статье рассмотрены некоторые приемы быстрых вычислений, которые могут пригодиться не только на уроках математики, но и в повседневной жизни.

Способы быстрого сложения чисел

Способы быстрого сложения чисел:

порядковое сложение чисел 15+39+26=(10+30+20)+(5=9+6)=60+20=80.

Прибавление к одному числу отдельных, разрядов другого числа, всегда начиная с высших:

Сложение с использованием свойств действий с числами

При выполнении быстрого сложения чисел самым простым, на мой взгляд, является прибавление к одному числу отдельных разрядов другого числа, всегда начиная с высших

Способы быстрого вычитания чисел

Способы быстрого вычитания:

Вычитание с использованием свойств действий с числами

Ученики чаще принимают метод с использованием свойств действий с числами.

Способы быстрого вычитания чисел

Вычитание путем уравнивания числа единиц последних разрядов уменьшаемого

Вычитание путем округления уменьшаемого или вычитаемого, или одновременно обоих.

Если уменьшаемое или вычитаемое близки, то их заменяют разностью или суммой между круглым числом и дополнением:

Удобно выполнять вычитание путем округления уменьшаемого или вычитаемого, или одновременно обоих:

Способы быстрого умножения чисел

Чтобы умножить число на однозначный множитель, умножают сначала десятки, затем единицы и оба результата складывают:

Умножение на двухзначное число.

Если оба множителя двухзначные числа, то разбиваем один из них на десятки и единицы. Разбивать надо множитель, у которого десятки и единицы выражены меньшими числами:

Индийская тайна быстрого умножения

Необходимо умножить два числа близкие к 100: 98х96

Найдем дополнения каждого множителя за 100 – соответственно 2 и 4.

Вычтем из 1-го множителя дополнения второго:

98-4=94 (или наоборот)

Это первые цифры произведения

Перемножим дополнения 2х4=8 (08) – это последние цифры произведения : 98х96=9408.

Умножение на 2 слева направо

При умножении на 2 запоминаем единицу, если цифра больше четырех, поэтому правило следующее: умножаем очередную цифру на 2 и произведение увеличиваем на единицу, когда последующая цифра больше 4, и записываем только цифру единицу результата, если это не первая цифра множителя; для первой цифры записываем полностью значение результата.

4286х2=8572, потому что 4х2=8 и пишем 8, так как последующая цифра не больше 4.

Далее: 2х2=4, следующая цифра больше 4, последнее произведение увеличиваем на единицу, и записываем 5.

Затем 8х2=16, но с учетом значения последней цифры, пишем 2: 5619х2=11238.

Действительно, 5х2=10, но следующая цифра больше 4, поэтому

Далее, 6х2=12, пишем только 2, так как последующая цифра меньше 4.

Далее, 1х2=2, но последующая цифра больше 4, поэтому пишем 3.

И наконец, 9х2=18, пишем 8.

Чтобы ускорить нахождение произведения, можно первый множитель разбить на грани, но несколько цифр в каждой последовательности умножаем числа каждой грани, записываем для первой грани полностью результат с учетом значения первой цифры следующей грани, для остальных граней записываем значение полученного результата, отбрасывая первую цифру, если число цифр результата больше числа цифр грани:

Разбиваем первый множитель на грани:

Далее, 32х2=64, но с учетом первой цифры следующей грани записываем 65. Затем 96х2=192 (количество цифр произведения 3, а грань состоит из двух цифр), первая цифра следующей грани не больше 4, поэтому записываем 92, затем записываем 90=45х2.

Способы быстрого умножения чисел.

Умножение на 4 и на 8

Чтобы число умножить на 4; 8, его последовательно удваивают:

Так как 5= 10/2, поэтому, чтобы умножить число на 5, нужно умножить его на 10 и разделить на 2, то есть к числу приписывают нуль и делят десять пополам:

Умножение на 0,5

Так как 0,5=1/2, поэтому чтобы умножить число на 0,5, его нужно разделить пополам:

Умножение на 1,5 и 15

Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину:

Чтобы число умножить на 15, нужно исходное число умножить на 10 и прибавить половину полученного произведения:

Часто в повседневной жизни нам приходится умножать число на 1,5 или на 15.

Это легко сделать так: 48х1,5=48+24=72;

Умножение на 15

Можно использовать соотношение 15=30/2, получаем, что ах15=ах30/2.

Предварительно представляем а, если оно нечетное, в виде суммы или разности нечетного числа и единицы:

Умножение на 11

Прием умножения на 11 поражает своей красотой.

36х11, для этого достаточно подписать 36 по 36, но сдвинув его на одну цифру вперед, вот так ₃₆

А затем выполнить сложение в столбик.

Эту операцию можно проводить с любыми цифрами, будь то трехзначное или четырехзначное число.

Умножить на 11 можно и другим способом. Достаточно «раздвинуть» числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем, если эта сумма больше 9, как при обычном сложении, следует единицу перенести в старший разряд.

На 11 умножить можно и так: приписать к умножаемому числу 0, а затем прибавить его:

Умножение на 25, 50, 75, 125

Принимая во внимание, что

Соответствующим образом преобразовываем второй множитель:

Приемы сокращенного умножения

На 5: 46х5=46/2х10=230;

На 25: 83х25=80/4х100+3х25=2075;

На 125: 48х125=48/8х1000=6000;

На 155: ах155=100а+50а+5а

Умножение двух чисел, «близких» к 100

Когда каждый из множителей меньше 100, тогда:

(100-а)(100- b )=100х100-100а-100 b +а b =(100-а- b )х100+ ab .

(100+а)(100+ b )=100(100+ a + b )+а b

Подсчитаем число сотен произведения 100-(а+ b )=100-11=89

Возведение в квадрат чисел,

цифра единиц которых равна пять

а5ха5=(10а+5)(10а+5)=100а 2 +2х10х5а+25=100(а 2 +а)+25=100ха(а+1)+25==(а(а+1))25.

Получаем правило: для умножения числа, которое заканчивается цифрой пять на само себя, необходимо число десятков умножить на последующее число и к полученному произведению приписать произведение цифр единиц, то есть 25.

Аналогичным образом находится произведение двух чисел, которых количество десятков одинаковое, а сумма цифр единиц равна десяти.

35х35=1225, так как 3х4=12;

125х125=15625, так как 12х13=156;

42х48=2016, так как 4х5=20 и 2х8=16.при возведении в квадрат любых чисел можно воспользоваться свойством:

а 2 =а 2 — b 2 + b 2 =(а- b )(а+ b )+ b 2

Обычно в качестве b выбираем такое число, чтобы а+ b и a — b было круглым числом.

76 2 =(76+4)(76-4)+4 2 =80х72+4 2 =5760+16=5760 ( b=4) ;

76 2 =(76+6)(76-6)+6 2 =82х70+36=5740+36=5776 ( b =6).

34 2 =(34+6)(34-6)+6 2 =40х28+36=1156;

987 2 =(987+13)(987-13)+13 2 =1000х974+169=974169.

Способы быстрого деления чисел.

Если делитель является составным числом, то разлагаем его на два или большее число множителей, а потом выполняем последовательное деление:

Нахождение частного, когда делитель равен 15, осуществляется по схеме:

Устный счет – это практическое явление, необходимое для развития вычислительных навыков и как следствие устной сдачи экзаменов.

Устное вычисление прекрасно стимулируют развитие памяти у детей и взрослых, увеличивают скорость мышления и улучшают сообразительность, тренируют внимание.

Школьники, развивающие навыки устного счета, очень быстро обгоняют по интеллекту своих одноклассников, полагающихся на калькуляторы.

Гибкость ума является предметом гордости людей, а способности производить быстрые вычисления в уме вызывают удивление.

Источник