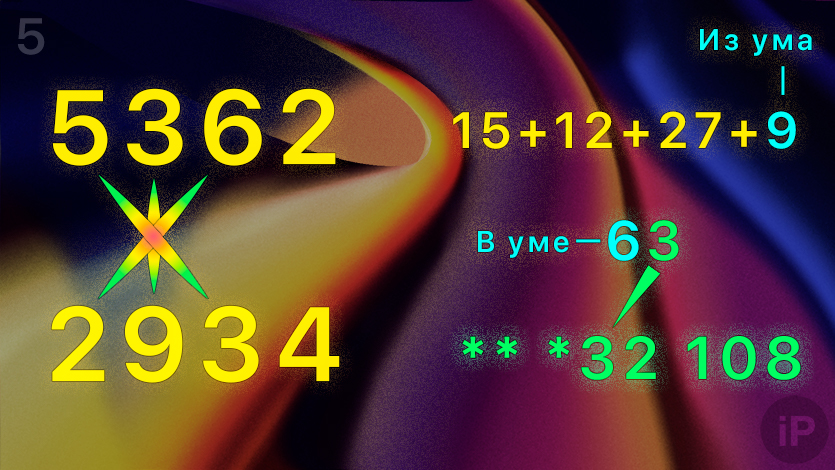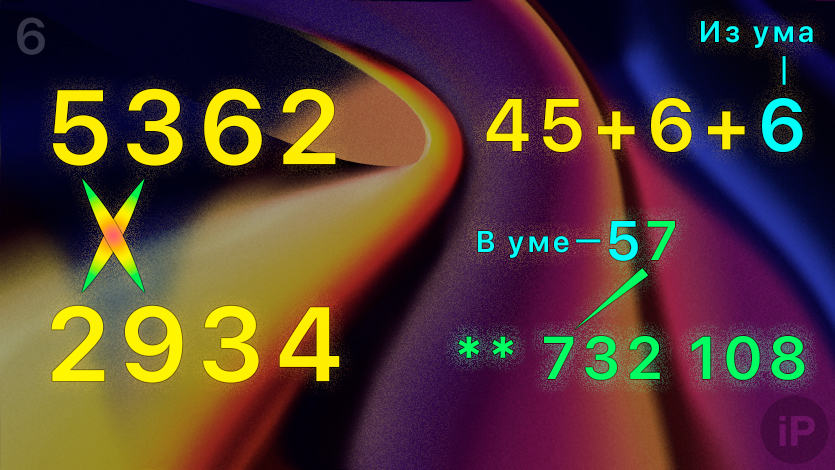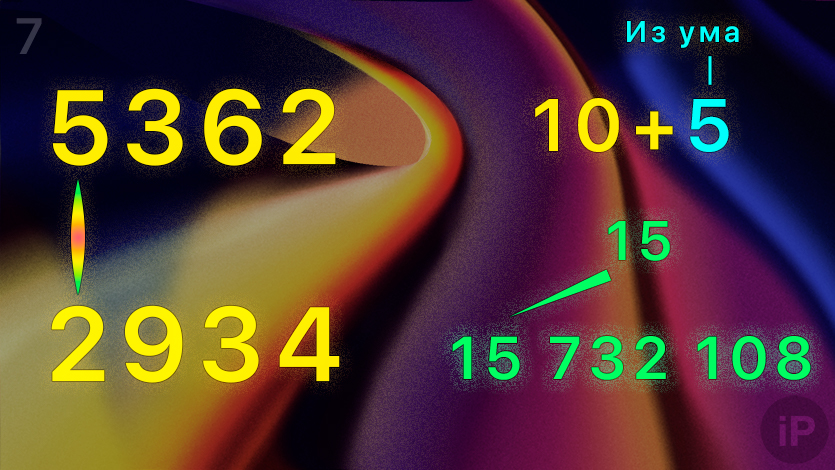Способы быстрого счета по трахтенбергу

Способы быстрого счета по трахтенбергу

Система Трахтенберга — система устного счёта, разработанная математиком Яковом Трахтенбергом во время заключения в нацистском концлагере. Состоит из нескольких частей — методов умножения на числа от 2 до 12, метода умножения произвольных натуральных чисел и другого.

Общее умножение

Пусть даны два числа — и , выглядящие в десятичной записи как и . Стандартный алгоритм умножения на предписывает умножить на все разряды по очереди и сложить результаты, учитывая их сдвиг. Трахтенберг предлагает взамен считать -ый разряд ответа как сумму переноса из предыдущего разряда и , не записывая промежуточные вычисления.

по дистрибутивности: слагаемые с влияют на разряд только в виде переноса, а с n>»/> — вообще не влияют.

Например, умножим 12345 на 21.

перенос		Всего	Цифра
0	5*1	5	5
0	4*1+5*2	14	4
1	3*1+4*2	12	2
1	2*1+3*2	9	9
0	1*1+2*2	5	5
0	1*2	2	2

Итого, читая снизу вверх, получается 259245. Яков Трахтенберг предлагает делать вычисления, записанные в таблице выше, в уме, выписывая только результат.

Частные правила умножения

Умножение на 11

Правило: Добавь цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 3425 × 11 = 37675

3425 × 11 = (0+3)(3+4)(4+2)(2+5)(5+0) = 37675

Умножение на 12

Правило: Добавь удвоенную цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 2413 × 12 = 28956

2413 × 12 = (0×2+2)(2×2+4)(4×2+1)(1×2+3)(3×2+0) = 28956

Умножение на 13

Правило: Добавь утроенную цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 5876 × 13 = 76388

5876 × 13 = (0×3+5)(5×3+8)(8×3+7)(7×3+6)(6×3+0) = 76388

Умножение на 14

Правило: Добавь учетверённую цифру к её соседу справа, не забывая про перенос через разряд.

Пример: 4859 × 14 = 68026

4859 × 14 = (0×4+4)(4×4+8)(8×4+5)(5×4+9)(9×4+0) = 68026

Умножение на 17

Правило: Добавь цифру, умноженную на разряд единиц, к её соседу справа, не забывая про перенос через разряд.

Пример: 5739 × 17 = 97563

5739 × 17 = (0×7+5)(5×7+7)(7×7+3)(3×7+9)(9×7+0) = 97563

Источник

Математическая система быстрого счета Трахтенберга, созданная в Освенциме

Благодаря Якову Трахтенбергу мир смогла увидеть одна из интереснейших и уникальнейших математических систем в мире. Но кто бы мог догадаться, что она была создана в Освенциме!

Нелёгкая судьба гения

Во время Второй Мировой войны вокруг царил хаос и ужас, Трахтенберга он, к сожалению, тоже не обошёл стороной. Из-за своего происхождения он был насильно доставлен из Берлина прямо в исток адских страданий – концентрационный лагерь. Ежедневно ему приходилось наблюдать за смертями своих соотечественников и издевательствами над ними, неоднократно подвергаясь им, в том числе. Чтобы не обезуметь, он решил полностью погрузиться в таинственный мир математики и чисел.

Найти даже клочок бумаги было непосильной задачей, однако, он искал выход из ситуации всеми возможными путями, насколько сложными они бы ни были. Но большинство информации он хранил не в рукописном варианте, а в своём разуме, что и сейчас позволяет проводить простые манипуляции с числами в уме и записывать лишь конечный результат.

Оперируя многозначными величинами, он задумывался, как упростить этот процесс и сделать его максимально простым и точным.

Продумывая множество вариантов, он, в конечном счёте, придумал поистине совершенный метод, который до сих пор часто используют в обиходе при тяжёлых подсчётах.

Удача наступает на пятки

Но как же в дальнейшем сложилась судьба такого талантливого человека?

Выждав подходящий момент, он смог совершить побег и выбраться из этого жерла вулкана отчаяния. Но он понимал, что стоит ему только попасться на глаза офицерам, и его ждёт та же участь. Так и произошло, однако в этот раз госпожа удача не обошла его стороной, офицер, который его поймал, оказалось, был знаком с деятельностью Якова. Избежать попадания в концлагерь ему не удалось, но он был доставлен в трудовой лагерь, который находился в Триесте. Да, работу на каменоломне лёгкой не назовёшь, но здесь охранники относились к узникам более снисходительно.

Трахтенберга не покидала мысль о побеге, и во второй раз он прошёл успешно. Он пришёл в себя уже в швейцарском лагере для беженцев. Оказавшись на свободе, он открыл институт математики, где и обучал своей методе детей.

Мир узнал об этой невероятной математической системе, благодаря счастливой случайности, по которой журналистка из США встретилась с гением. Она была в восторге, когда увидела, что даже ребёнок может производить сложнейшие расчёты, используя метод Трахтенберга.

Способы и примеры умножения по методике Трахтенберга

Она была знакома с одним из талантливейших профессоров математики Рудольфом МакШэйном, вместе с которым в дальнейшем Яков издал учебник-книгу для старшеклассников и студентов «Быстрая система элементарной математики Трахтенберга». Выше кратко изложена система быстрого счета по Трахтенбергу.

В ходе дальнейших исследований он определил, что его система помогает улучшать память без лишних усилий и укреплять разум. А сейчас его изобретение используют даже в банках и больших компаниях, это явный показатель того, что её оценили по достоинству.

Источник

Эта инструкция научит вас умножать тысячи в уме. Сколько будет 5185 на 8018?

В школе всё время слышал «где мне пригодится эта математика?».

И сам задавался таким вопросом. А сейчас вот не хватает учебника для «раскачки» извилин. Например, было бы заметно удобнее считать утерянные цены на Apple или выравнивать пиксельную сетку для иллюстраций.

Но не всё потеряно. Умножать числа в любом возрасте считают проверенным способом подточить ум и даже улучшить психическое здоровье.

Ниже расскажу, где оно ещё может пригодиться и что за секретный способ умножения прокачает ваше знание цифр до уровня интуиции.

Крупный счёт прокачает решение бытовых вопросов

Как любому компьютеру нужно расширять оперативную память, так и нашему мозгу нужен отсек для быстрых операций.

Тренировки с умножением укрепят краткосрочную память. Вы перестанете забывать, закрыли ли дверь на ключ, сколько яиц лежало в холодильнике перед походом в магазин и о чём вели речь после того, как отвлеклись.

Не говоря о том, что будете мгновенно считать, во сколько обойдётся вон тот сочный кусок мяса на шашлык или заправка автомобиля, чтобы доехать до соседнего города.

Вам нужна только математика начальной школы

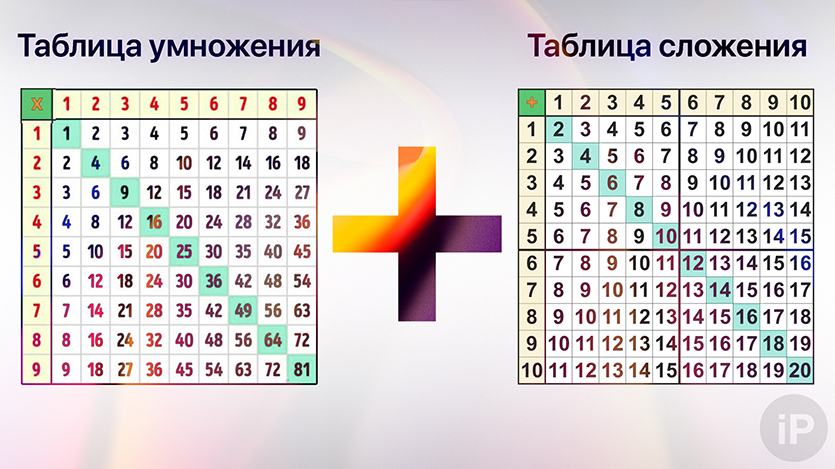
Чтобы умножать без бумаги, нужно на уровне рефлекса освоить два навыка:

I. Знать таблицу умножения
II. Складывать числа

Пункты важны, потому что будете десятки раз повторять операции. Получается просто, но много.

Отточить умножение поможет приложение УмноЖатель

Уделяйте тренировке не больше пяти минут за подход. Потом запоминать сложнее, а после тройки долгих сессий цифры начнут раздражать.

Быстро складывать получится точно таким же постоянным запоминанием.

Почти нигде не просят знать таблицу сложения, а она есть. Если до десяти цифры знают почти все, то после этого порога начинается ступор.

На лету вспомнить, какое число будет в следующем десятке полезнее в жизни, чем любое другое вычисление. Поэтому качайте и запоминайте.

Ещё один способ сложения, которого некоторые стесняются – довод до десятка. Это когда к одному числу сначала добавляют до круглого значения часть из второго, а потом плюсуют остаток:

8+5 = 8+2+3 = 10+3 = 13

В этом способе нет ничего стыдного, он эффективен, и с практикой доводится до автоматизма.

Когда научитесь на лету умножать и складывать элементарные значения, вставайте на продвинутый уровень: расчёты четырёхзначных чисел.

Операции с умножением тысячей в уме можно разделить на два типа: умножение на однозначные и многозначные числа.

Как умножить тысячи на однозначное число

Чтобы получить ответ на, допустим, пример 3864∙7, вам поможет система Разбить-умножить, разбить-сложить.

Так выглядит алгоритм:

1. Разбиваем большое число на единицы, десятки, сотни и так далее.

3864 = 3000 + 800 + 60 + 4

2. Умножаем каждый кусочек на второе число.

3000∙7 = 21000 | 800∙7 = 5600 | 60∙7 = 420 | 4∙7 = 28

3. Разбиваем результаты на простые группы одного размера.

21000 = 20000+1000 | 5600=5000+600 | 420 = 400+20 | 28 = 20+8

20000 | 1000+5000 | 600+400 | 20+20 | 8

4. Складываем группы с конца.

20000 + 1000+5000 + 600+400 + 20+20 + 8

20000 + 6000 + 1000 + 40 + 8

Хотя на бумаге способ получается долгим, через несколько дней тренировка даст заметные результаты в скорости. У вас улучшится краткосрочная память, и вместимость чисел для сложения постепенно увеличится.

Важнее всего не потерять куски при последнем сложении. Этот этап доведёте до автомата постоянной практикой.

Отличие метода от привычного столбика в том, что мы постоянно дробим элементы на лёгкие частицы, которые быстро складываются.

Как умножить тысячи на многозначное число

Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.

Предупреждаю, что способ подойдёт только тем, кто наработал краткосрочную память на большой массив чисел . Поскольку вам придётся долго держать остаток в уме и параллельно делать десяток сложений.

Запомните метод как Принцип снежинки.

В качестве примера решим 5362∙2934. Алгоритм такой:

0. Представьте числа привычным столбиком.

1. Перемножьте конечные (2∙4) цифры сверху и снизу.

Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.

2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).

Сложите результаты с тем, что храните в уме (24+6+0=30).

Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.

3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).

Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).

Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.

4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).

Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).

Сложите четыре числа и пятое из ума (20+4+9+54+5=92).

Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.

5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).

Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).

Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.

6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).

Сложите результаты с остатком в уме (45+6+6=57).

Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.

7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).

Сложите результат с остатком в уме (10+5=15).

Запишите всё число перед итоговым: 15 732 108.

Вы получили ответ.

Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.

Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.

Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.

Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.

Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.

И тогда сможете считать миллионы, не коснувшись бумаги.

Источник