infoegehelp.ru
Быстрый перевод числа из десятичной системы счисления в двоичную
Чтобы быстро переводить числа из десятичной системы счисления в двоичную, нужно хорошо знать числа «2 в степени». Например, 2 10 =1024 и т.д. Это позволит решать некоторые примеры на перевод буквально за секунды. Одной из таких задач является задача A1 из демо ЕГЭ 2012 года. Можно, конечно, долго и нудно делить число на «2». Но лучше решать по-другому, экономя драгоценное время на экзамене.
Метод очень простой. Суть его такая: если число, которое нужно перевести из десятичной системы, равно числу «2 в степени», то это число в двоичной системе содержит количество нулей, равное степени. Впереди этих нулей добавляем «1».
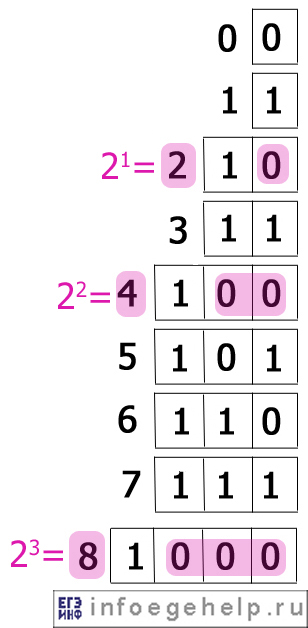
- Переведем число 2 из десятичной системы. 2=2 1 . Поэтому в двоичной системе число содержит 1 нуль . Впереди ставим «1» и получаем 1 0 2.
- Переведем 4 из десятичной системы. 4=2 2 . Поэтому в двоичной системе число содержит 2 нуля . Впереди ставим «1» и получаем 1 00 2.
- Переведем 8 из десятичной системы. 8=2 3 . Поэтому в двоичной системе число содержит 3 нуля . Впереди ставим «1» и получаем 1 000 2.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Аналогично и для других чисел «2 в степени».
Если число, которое нужно перевести, меньше числа «2 в степени» на 1, то в двоичной системе это число состоит только из единиц, количество которых равно степени.
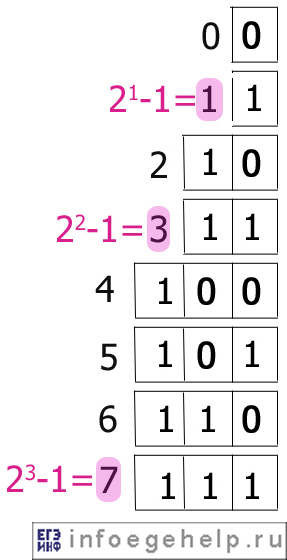
- Переведем 3 из десятичной системы. 3=2 2 -1. Поэтому в двоичной системе число содержит 2 единицы . Получаем 11 2.
- Переведем 7 из десятичной системы. 7=2 3 -1. Поэтому в двоичной системе число содержит 3 единицы . Получаем 111 2.
На рисунке квадратиками обозначено двоичное представление числа, а слева розовым цветом-десятичное.
Аналогичен перевод и для других чисел «2 в степени-1».
Понятно, что перевод чисел от 0 до 8 можно сделать быстро или делением, или просто знать наизусть их представление в двоичной системе. Я привела эти примеры, чтобы Вы поняли принцип данного метода и использовали его для перевода более «внушительных чисел», например, для перевода чисел 127,128, 255, 256, 511, 512 и т.д.
Можно встретить такие задачи, когда нужно перевести число, не равное числу «2 в степени», но близкое к нему. Оно может быть больше или меньше числа «2 в степени». Разница между переводимым числом и числом «2 в степени» должна быть небольшая. Например, до 3. Представление чисел от 0 до 3 в двоичной системе надо просто знать без перевода.
Если число больше , то решаем так:
Переводим сначала число «2 в степени» в двоичную систему. А потом прибавляем к нему разницу между числом «2 в степени» и переводимым числом.
Например, переведем 19 из десятичной системы. Оно больше числа «2 в степени» на 3.
Если число меньше числа «2 в степени», то удобнее пользоваться числом «2 в степени-1». Решаем так:
Переводим сначала число «2 в степени-1» в двоичную систему. А потом вычитаем из него разницу между числом «2 в степени-1» и переводимым числом.
Например, переведем 29 из десятичной системы. Оно больше числа «2 в степени-1» на 2. 29=31-2.
Если разница между переводимым числом и числом «2 в степени» больше трех , то можно разбить число на составляющие, перевести каждую часть в двоичную систему и сложить.
Например, перевести число 528 из десятичной системы. 528=512+16. Переводим отдельно 512 и 16.
512=2 9 . 51210=1 000000000 2.
16=2 4 . 1610=1 0000 2.
Теперь сложим столбиком:
Данная методика позволяет тратить минимум времени на перевод чисел из десятичной системы в двоичную, но при условии, что Вы прекрасно знаете числа «2 в степени». Если это не так, то заучите эти числа. Тем более, что в задачах по информатике они активно используются.
Учить числа «2 в степени» удобно по этому материалу
Источник
Способы перевода чисел из одной системы счисления в другую
Сдающим ЕГЭ и не только…
Странно, что в школах на уроках информатики обычно показывают ученикам самый сложный и неудобный способ перевода чисел из одной системы в другую. Это способ заключается в последовательном делении исходного числа на основание и сборе остатков от деления в обратном порядке.
Например, нужно перевести число 81010 в двоичную систему:

Результат записываем в обратном порядке снизу вверх. Получается 81010 = 11001010102
Если нужно переводить в двоичную систему довольно большие числа, то лестница делений приобретает размер многоэтажного дома. И как тут собрать все единички с нулями и ни одной не пропустить?
В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7.
Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией.
Таблица степеней числа 2:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 | 2 8 | 2 9 | 2 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Она легко получается умножением предыдущего числа на 2. Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Таблица двоичных чисел от 0 до 15 c 16-ричным представлением:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.
Перевод целых чисел
Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число 81010. Нам нужно разложить это число на слагаемые, равные степеням двойки.
- Ищем ближайшую к 810 степень двойки, не превосходящую его. Это 2 9 = 512.
- Вычитаем 512 из 810, получаем 298.
- Повторим шаги 1 и 2, пока не останется 1 или 0.
- У нас получилось так: 810 = 512 + 256 + 32 + 8 + 2 = 2 9 + 2 8 + 2 5 + 2 3 + 2 1 .
Далее есть два способа, можно использовать любой из них. Как легко увидеть, что в любой системе счисления её основание всегда 10. Квадрат основания всегда будет 100, куб 1000. То есть степень основания системы счисления — это 1 (единица), и за ней столько нулей, какова степень.
Способ 1: Расставить 1 по тем разрядам, какие получились показатели у слагаемых. В нашем примере это 9, 8, 5, 3 и 1. В остальных местах будут стоять нули. Итак, мы получили двоичное представление числа 81010 = 11001010102 . Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Способ 2: Распишем слагаемые как степени двойки друг под другом, начиная с большего.
810 =
| 2 9 = | 1000000000 | (1 и девять нулей) + |
| 2 8 = | 100000000 | (1 и восемь нулей) + |
| 2 5 = | 100000 | (1 и пять нулей) + |
| 2 3 = | 1000 | (1 и три нуля) + |
| 2 1 = | 10 | (1 и один ноль) |
А теперь сложим эти ступеньки вместе, как складывают веер: 1100101010 .
Вот и всё. Попутно также просто решается задача «сколько единиц в двоичной записи числа 810?».
Ответ — столько, сколько слагаемых (степеней двойки) в таком его представлении. У 810 их 5.
Теперь пример попроще.
Переведём число 63 в 5-ричную систему счисления. Ближайшая к 63 степень числа 5 — это 25 (квадрат 5). Куб (125) будет уже много. То есть 63 лежит между квадратом 5 и кубом. Тогда подберем коэффициент для 5 2 . Это 2.
Получаем 6310 = 50 + 13 = 50 + 10 + 3 = 2 * 5 2 + 2 * 5 + 3 = 2235 .
Ну и, наконец, совсем лёгкие переводы между 8- и 16-ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
Переведем в двоичную систему число 5478.
| 5478= | 101 | 100 | 111 |
| 5 | 4 | 7 |
Ещё одно, например 7D6A16.
| 7D6A16= | (0)111 | 1101 | 0110 | 1010 |
| 7 | D | 6 | A |
Переведем в 16-ричную систему число 7368. Сначала цифры запишем тройками, а потом поделим их на четверки с конца: 7368 = 111 011 110 = 1 1101 1110 = 1DE16 . Переведем в 8-ричную систему число C2516. Сначала цифры запишем четвёрками, а потом поделим их на тройки с конца: C2516 = 1100 0010 0101 = 110 000 100 101 = 60458 . Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем. E6816 = 14 * 16 2 + 6 * 16 + 8 = 3688 . 7328 = 7 * 8 2 + 3*8 + 2 = 474 .
Перевод отрицательных чисел
Здесь нужно учесть, что число будет представлено в дополнительном коде. Для перевода числа в дополнительный код нужно знать конечный размер числа, то есть во что мы хотим его вписать — в байт, в два байта, в четыре. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом. Беззнаковые (unsigned) числа мы не рассматриваем, они всегда положительные, а старший разряд в них используется как информационный.
Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.
Итак, переведем число -79 в двоичную систему. Число займёт у нас один байт.
Переводим 79 в двоичную систему, 79 = 1001111. Дополним слева нулями до размера байта, 8 разрядов, получаем 01001111. Меняем 1 на 0 и 0 на 1. Получаем 10110000. К результату прибавляем 1, получаем ответ 10110001 . Попутно отвечаем на вопрос ЕГЭ «сколько единиц в двоичном представлении числа -79?». Ответ — 4.
Прибавление 1 к инверсии числа позволяет устранить разницу между представлениями +0 = 00000000 и -0 = 11111111. В дополнительном коде они будут записаны одинаково 00000000.
Перевод дробных чисел
Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале. То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.
Переведем число 0,6752 в двоичную систему.
| 0 | ,6752 |
| *2 | |
| 1 | ,3504 |
| *2 | |
| 0 | ,7008 |
| *2 | |
| 1 | ,4016 |
| *2 | |
| 0 | ,8032 |
| *2 | |
| 1 | ,6064 |
| *2 | |
| 1 | ,2128 |
Процесс можно продолжать долго, пока не получим все нули в дробной части или будет достигнута требуемая точность. Остановимся пока на 6-м знаке.
Получается 0,6752 = 0,101011 .
Если число было 5,6752, то в двоичном виде оно будет 101,101011 .
Источник
Урок 14
§11.5. «Быстрый» перевод чисел в компьютерных системах счисления
Содержание урока:
| 11.5. «Быстрый» перевод чисел в компьютерных системах счисления |  |
 | Примеры 7 и 8 |
11.5. «Быстрый» перевод чисел в компьютерных системах счисления
Из курса информатики основной школы вы знаете, что в компьютерных науках широко используются двоичная, восьмеричная и шестнадцатеричная системы счисления, благодаря чему их называют «компьютерными».
Между основаниями этих систем существует очевидная связь: 16 = 2 4 , 8 = 2 3 .
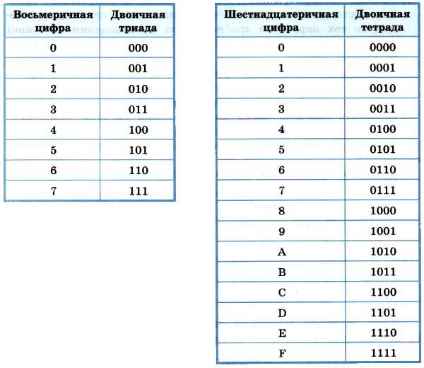
Способ «быстрого» перевода основан на том, что каждой цифре числа в системе счисления, основание которой q кратно степени двойки, соответствует число, состоящее из n (q = 2 n ) цифр в двоичной системе счисления. Замена восьмеричных цифр двоичными тройками (триадами) и шестнадцатеричных цифр двоичными четвёрками (тетрадами) позволяет осуществлять быстрый перевод между этими системами счисления, не прибегая к арифметическим операциям.
Для того чтобы целое двоичное число записать в системе счисления с основанием q = 2 n , достаточно:
1) данное двоичное число разбить справа налево на группы по n цифр в каждой;
2) если в последней левой группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов;
3) рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой системы счисления с основанием q = 2 n .
Cкачать материалы урока
Источник