Способы борьбы с коллизиями

Особенности применения норм права при коллизиях в позитивном праве

Коллизия – столкновение между действующими нормами, по-разному регулирующими одно и то же правоотношение (т.е. налицо противоречие).

Причины возникновения коллизий:

А) Объективные (правоотношения нередко бывают вытянуты не только во времени, но и в пространстве, следовательно, могут одновременно подпадать под юрисдикцию разных субъектов правотворчества, которые по-разному регулируют эти правоотношений, в связи с этим и появляются коллизии).

Б) Субъективные(связаны с изъянами в процессе правотворчества в юридической техники, хотя могут иметь и умышленный характер).

Виды коллизий: (в зависимости от характера):

1) иерархические (имеет место тогда, когда между собой конкурируют нормы, обладающие разной юридической силой);

2) содержательные (имеет место тогда, когда между собой конкурируют общие, специальные и исключительные нормы, обладающие одинаковой юридической силой);

3) темпаральные или временные (имеет место тогда, когда между собой конкурируют обладающие одинаковой юридической силой нормы, вступившие в силу в разные периоды времени);

4) пространственные или территориальные (имеет место тогда, когда вытянутое в пространстве правоотношение подпадает под юрисдикцию разных субъектов правотворчества).

Способы борьбы с коллизиями:

Чтобы устранить коллизии на практике используются специальные нормы, получившие наименование «коллизионных» норм. Они могут быть официально закреплены в соответствующих источниках (в законодательстве, в различных кодексах, в Конституции Российской Федерации), но могут и нигде не закреплены официально (формулируются учеными, юристами-практиками).

1) иерархические коллизионные нормы. Это самый простой вид коллизии. При конкуренции норм различной юридической силы используется та норма, что обладает наибольшей юридической силой (часть 3, 5, 6 статьи 76 К РФ). Все остальные виды коллизии усложняются тем, что устанавливаются одинаковой юридической силой. 2) содержательные коллизионные нормы. Не существует единой нормы, которая регулировала бы все содержательные коллизии. Они зависят от того, где расположены коллизионные юридические нормы. Если конкурирующие нормы, закрепленные в одном нормативном акте, то действует правило «специальные нормы обладают приоритетом перед общими, а исключительные нормы обладает приоритетом перед специальными и перед общими». Если номы расположены в разных юридических источниках, то действует правило «наибольшей юридической силой обладает общая норма, затем норма исключительная, а после специальная». 3) темпаральные (временные) коллизионные нормы. Здесь действует правило «реализации подлежит та норма, которая вступила в действие позднее» (например, Трудовой Кодекс РФ часть 2 статья 12). Предполагается, что в более поздней норме воля законодателя закреплена более полно. 4) пространственные (территориальные) коллизионные нормы. Наиболее часто встречаются в федеративных государствах и международном праве. Единых для всего населения пространственных коллизионных норм не существует, следовательно, обращаясь к ним нужно каждый раз рассматривать позитивное право (ст. 18 Основ Гражданского Законодательства).

Источник

43. Коллизии в праве. Способы преодоления и устранение коллизий

Юридические коллизии — это противоречия между правовыми актами, регулирующими одни и те же общественные отношения. Они вносят в правовую систему несогласованность, создают неудобства в правоприменительной практике, затрудняют пользование законодательством.

Можно выделить объективные причины коллизий (например. в условиях отставания права от более динамичных общественных отношений одни нормы «устаревают», другие же — принимаются и действуют одновременно без отмены прежних) и субъективные (недостаток опыта законодателя, низкое качество законов, непоследовательная систематизация нормативных актов и пр.).

Коллизии могут возникать:

1) между конституцией и иными актами (разрешаются в пользу конституции);

2) между законами и подзаконными актами (разрешается в пользу законов, как актов большей юридической силы);

3) между общефедеральными актами и актами субъектов Федерации:

если последний принят в пределах ведения, то в соответствии с ч. 6 ст. 76 Конституции РФ действует именно он;

если последний принят вне пределов своего ведения, то действует общефедеральный акт;

4) между актами одного и того же органа, но изданным в различное время (применяется позже принятый акт);

5) между актами, принятыми разными органами (применяется акт, обладающий большей юридической силой;

6) между общим и специальным актом:

— если они приняты одним органом, то применяется последний;

— если они приняты разными органами, то действует первый.

Возможные способы разрешения коллизий:

— принятие нового акта;

— отмена старого акта;

— внесение изменений в действующие акты;

— переговорный процесс через согласительные комиссии;

— толкование и др.

44-45. Толкование права: понятие и виды

Применение правовых норм невозможно без предварительного познания смысла юридических установлений. Как справедливо замечено, регламентация общественных отношений может считаться законченной лишь тогда, когда их участники уяснили содержание юридических правил. Толкование норм права, таким образом, — важное условие их действенности. Для правоприменительных органов, кроме того, неправильное истолкование юридических предписаний влечет нарушение законности, есть достаточное основание для отмены или изменения вынесенного решения.

Толкование норм права — это деятельность, направленная на установление содержания юридических норм. В процессе толкования уясняется смысл нормативного предписания, его социальная направленность, место в системе правового регулирования и т.п.

Толкование необходимо в связи:

1) с абстрактностью юридических норм (если нормы права имеют общий характер, то сами социальные отношения, которые они при званы регулировать, имеют конкретный характер; поэтому всегда необходимо знать, распространяется ли данная абстрактная норма на ту или иную ситуацию);

2) со специальной терминологией (в процесс е формулирования юридических норм законодатель вынужден использовать множество сугубо специальных юридических терминов — «моральный вред», «залог», «доверительное управление», «крайняя необходимость», «необходимая оборона» и т.п., — иначе невозможно создать общее правило поведения, а также специальных терминов из других отраслей знания — «эвтаназия», «токсичность» и др.);

3) с использованием в законодательстве ряда оценочных понятий — «существенный вред», «малозначительное деяние», «сильное душевное волнение» и пр.;

4) с дефектностью правотворческого процесса (неясностью и т.д.).

Деятельность по толкованию правовых норм имеет целью пра.вильное и единообразное понимание юридических предписаний и их правильное и единообразное применение.

Понятием «толкование» охватывается как уяснение (для себя), так и разъяснение (для других).

В зависимости от субъектов толкование подразделяют на:

— — официальное (дается уполномоченными на то субъектами, содержится в специальном акте, влечет юридические последствия);

— — неофициальное (не имеет юридически обязательного значения и лишено властной силы).

Официальное толкование бывает нормативным (распространяется на большой круг лиц и случаев, например, руководящие разъяснения Пленума Верховного Суда РФ) и казуальным(обязательно только для данного конкретного случая, например, приговор суда, в котором обосновывается мера наказания в отношении осужденного, указываются смягчающие или отягчающие вину обстоятельства). В свою очередь нормативное толкование классифицируется на аутентичное (дается тем же органом, который издал нормативный акт, например, Государственная Дума РФ принимает федеральные законы и их же разъясняет) и легальное (исходитот уполномоченных на то субъектов, например от Конституционного Суда РФ).

Неофициальное толкование бывает:

1) обыденным (не требует специальных познаний и дается любым гражданином);

2) профессиональным (дают юристы — судьи, прокуроры, нотариусы, следователи, адвокаты и т.п.);

3) доктринальным (научное разъяснение юридических норм, даваемое учеными-юристами в статьях, монографиях, комментариях, на лекциях, конференциях, «круглых столах и т.д.; его значение определяется убедительностью и авторитетом тех субъектов, которые осуществляют данное толкование).

Неофициальное толкование по форме выражения может быть как устным (разъяснение какого-либо юридического предписания адвокатом, судьей, прокурором в ходе приема граждан, на лекциях и т.п.), так и письменным (в периодической печати, в различных комментариях). Хотя такое разъяснение не имеет юридической силы, оно оказывает значительное влияние на правовую жизнь общества, в первую очередь на правотворческий и правореализационный процессы через правосознание соответствующих субъектов.

Способы толкования — это, совокупность приемов и средств, направленных на установление содержания правовых норм.

Выделяют следующие способы:

— грамматический (толкование с помощью языковых средств, правил грамматики, орфографии и т.п.; хрестоматийным примером здесь может выступать известная фраза: «казнить нельзя помиловать»;

— логический (толкование с помощью законов и правил логики);

— систематический (толкование с помощью анализа системных связей юридической нормы с другими нормами, места и роли конкретного правила поведения в системе права);

— историко-политический (толкование с помощью анализа конкретно-исторических и политических условий принятия правовой нормы);

— телеологический (толкование с помощью установления целей издания нормативного акта);

— специально-юридический (толкование с помощью раскры тия содержания юридических терминов, используемых в законодательстве).

Результаты толкования могут быть различными в зависимости от соотношения текста и действительного содержания юридических норм. Исходя из этого различают три вида толкования:

— буквальное (возможно в случаях, когда действительный смысл нормы права и ее текстуальное выражение совпадают; например, используемые в законодательстве термины «родители», «детей» должны пониматься в обыденном смысле);

— ограничительное (применяется, если действительный смысл нормы права уже ее текстуального выражения. Так, согласно п. 1 ст. 34 Семейного кодекса РФ «имущество, нажитое супругами во время брака, является их совместной собственностью». Однако нередки случаи, когда супруги, не расторгнув брака, проживают раздельно. Является ли при таких условиях нажитое ими имущество совместным? В данном случае, видимо, необходимо толковать нормы права ограничительно, т.е. не всякое имущество, нажитое во время брака, является совместной собственностью);

— распространительное (применяется, когда действительный смысл нормы права шире ее текстуального выражения. Примером может служить ч. 1 ст. 120 Конституции РФ, в которой установлено, что «судьи независимы и подчиняются только Конституции Российской Федерации и федеральному закону». Если применить буквальное толкование, то судьи не подчиняются федеральным конституционным законам, указам Президента и иным актам. Однако данную статью необходимо толковать шире: судьи подчиняются всей системе нормативных актов, действующих в государстве).

Источник

Разрешение коллизий

Разрешение коллизий (англ. collision resolution) в хеш-таблице, задача, решаемая несколькими способами: метод цепочек, открытая адресация и т.д. Очень важно сводить количество коллизий к минимуму, так как это увеличивает время работы с хеш-таблицами.

Содержание

Разрешение коллизий с помощью цепочек [ править ]

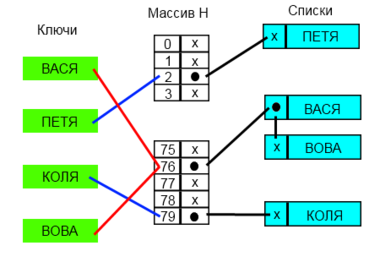
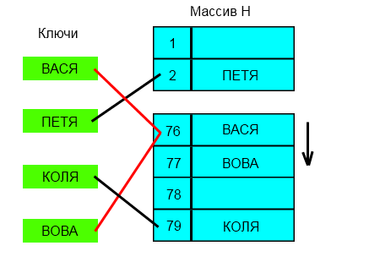
Каждая ячейка [math]i[/math] массива [math]H[/math] содержит указатель на начало списка всех элементов, хеш-код которых равен [math]i[/math] , либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.

В зависимости от того нужна ли нам уникальность значений операции вставки у нас будет работать за разное время. Если не важна, то мы используем список, время вставки в который будет в худшем случае равна [math]O(1)[/math] . Иначе мы проверяем есть ли в списке данный элемент, а потом в случае его отсутствия мы его добавляем. В таком случае вставка элемента в худшем случае будет выполнена за [math]O(n)[/math]

Время работы поиска в наихудшем случае пропорционально длине списка, а если все [math]n[/math] ключей захешировались в одну и ту же ячейку (создав список длиной [math]n[/math] ) время поиска будет равно [math]\Theta(n)[/math] плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех [math]n[/math] элементов.

Удаления элемента может быть выполнено за [math]O(1)[/math] , как и вставка, при использовании двухсвязного списка.

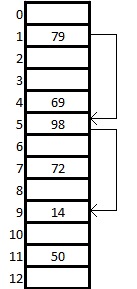
Линейное разрешение коллизий [ править ]

Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличие от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно, будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.

Стратегии поиска [ править ]

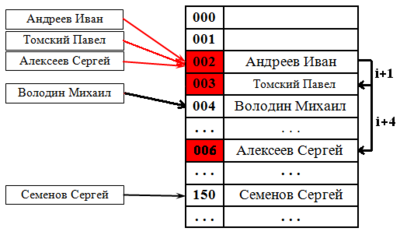
При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+1, i+2, i+3[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.

Выбираем шаг [math]q[/math] . При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск — частный случай линейного, где [math]q=1[/math] .

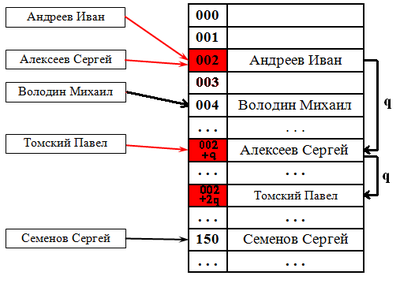
Шаг [math]q[/math] не фиксирован, а изменяется квадратично: [math]q = 1,4,9,16. [/math] . Соответственно при попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math] i+1, i+4, i+9[/math] и так далее, пока не найдём свободную ячейку.

Проверка наличия элемента в таблице [ править ]

Проверка осуществляется аналогично добавлению: мы проверяем ячейку [math]i[/math] и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.

При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.

Проблемы данных стратегий [ править ]

Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.

Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.

Удаление элемента без пометок [ править ]

Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на [math]q[/math] позиций назад. При этом:

• если в цепочке встречается элемент с другим хешем, то он должен остаться на своём месте (такая ситуация может возникнуть если оставшаяся часть цепочки была добавлена позже этого элемента)
• в цепочке не должно оставаться «дырок», тогда любой элемент с данным хешем будет доступен из начала цепи

Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).

Хеш-таблицу считаем зацикленной

Утверждение (о времени работы):

[math]\triangleright[/math]

Заметим что указатель [math]j[/math] в каждой итерации перемещается вперёд на [math]q[/math] (с учётом рекурсивных вызовов [math]\mathrm[/math] ). То есть этот алгоритм последовательно пройдёт по цепочке от удаляемого элемента до последнего — с учётом вызова [math]\mathrm[/math] собственно для нахождения удаляемого элемента, мы посетим все ячейки цепи.

[math]\triangleleft[/math]

Вариант с зацикливанием мы не рассматриваем, поскольку если [math]q[/math] взаимнопросто с размером хеш-таблицы, то для зацикливания в ней вообще не должно быть свободных позиций

Теперь докажем почему этот алгоритм работает. Собственно нам требуется сохранение трёх условий.

• В редактируемой цепи не остаётся дырок

Докажем по индукции. Если на данной итерации мы просто удаляем элемент (база), то после него ничего нет, всё верно. Если же нет, то вызванный в конце [math]\mathrm[/math] (см. псевдокод) заметёт созданную дыру (скопированный элемент), и сам, по предположению, новых не создаст.

• Элементы, которые уже на своих местах, не должны быть сдвинуты.

• В других цепочках не появятся дыры

Противное возможно только в том случае, если какой-то элемент был действительно удалён. Удаляем мы только последнюю ячейку в цепи, и если бы на её месте возникла дыра для сторонней цепочки, это бы означало что элемент, стоящий на [math]q[/math] позиций назад, одновременно принадлежал нашей и другой цепочкам, что невозможно.

Двойное хеширование [ править ]

Двойное хеширование (англ. double hashing) — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.

Принцип двойного хеширования [ править ]

При двойном хешировании используются две независимые хеш-функции [math] h_1(k) [/math] и [math] h_2(k) [/math] . Пусть [math] k [/math] — это наш ключ, [math] m [/math] — размер нашей таблицы, [math]n \bmod m [/math] — остаток от деления [math] n [/math] на [math] m [/math] , тогда сначала исследуется ячейка с адресом [math] h_1(k) [/math] , если она уже занята, то рассматривается [math] (h_1(k) + h_2(k)) \bmod m [/math] , затем [math] (h_1(k) + 2 \cdot h_2(k)) \bmod m [/math] и так далее. В общем случае идёт проверка последовательности ячеек [math] (h_1(k) + i \cdot h_2(k)) \bmod m [/math] где [math] i = (0, 1, \; . \;, m — 1) [/math]

Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за [math]O(1)[/math] , в худшем — за [math]O(m)[/math] , что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.

[math]\forall x \neq y \; \exists h_1,h_2 : p(h_1(x)=h_1(y))\gt p((h_1(x)=h_1(y)) \land (h_2(x)=h_2(y)))[/math]

Выбор хеш-функций [ править ]

[math] h_1 [/math] может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, [math] h_2 [/math] должна возвращать значения:

• не равные [math] 0 [/math]
• независимые от [math] h_1 [/math]
• взаимно простые с величиной хеш-таблицы

Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а [math] h_2 [/math] возвращает натуральные числа, меньшие [math] m [/math] . Второй — размер таблицы является степенью двойки, а [math] h_2 [/math] возвращает нечетные значения.

Например, если размер таблицы равен [math] m [/math] , то в качестве [math] h_2 [/math] можно использовать функцию вида [math] h_2(k) = k \bmod (m-1) + 1 [/math]

Пример [ править ]

Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:

[math] h(k,i) = (h_1(k) + i \cdot h_2(k)) \bmod 13 [/math]

[math] h_1(k) = k \bmod 13 [/math]

[math] h_2(k) = 1 + k \bmod 11 [/math]

Мы хотим вставить ключ 14. Изначально [math] i = 0 [/math] . Тогда [math] h(14,0) = (h_1(14) + 0\cdot h_2(14)) \bmod 13 = 1 [/math] . Но ячейка с индексом 1 занята, поэтому увеличиваем [math] i [/math] на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При [math] i = 2 [/math] получаем [math] h(14,2) = (h_1(14) + 2\cdot h_2(14)) \bmod 13 = 9 [/math] . Ячейка с номером 9 свободна, значит записываем туда наш ключ.

Таким образом, основная особенность двойного хеширования состоит в том, что при различных [math] k [/math] пара [math] (h_1(k),h_2(k)) [/math] дает различные последовательности ячеек для исследования.

Простая реализация [ править ]

Пусть у нас есть некоторый объект [math] item [/math] , в котором определено поле [math] key [/math] , от которого можно вычислить хеш-функции [math] h_1(key)[/math] и [math] h_2(key) [/math]

Так же у нас есть таблица [math] table [/math] величиной [math] m [/math] , состоящая из объектов типа [math] item [/math] .

Реализация с удалением [ править ]

Чтобы наша хеш-таблица поддерживала удаление, требуется добавить массив [math]deleted[/math] типов [math]bool[/math] , равный по величине массиву [math]table[/math] . Теперь при удалении мы просто будем помечать наш объект как удалённый, а при добавлении как не удалённый и замещать новым добавляемым объектом. При поиске, помимо равенства ключей, мы смотрим, удалён ли элемент, если да, то идём дальше.

Альтернативная реализация метода цепочек [ править ]

В Java 8 для разрешения коллизий используется модифицированный метод цепочек. Суть его заключается в том, что когда количество элементов в корзине превышает определенное значение, данная корзина переходит от использования связного списка к использованию сбалансированного дерева. Но данный метод имеет смысл лишь тогда, когда на элементах хеш-таблицы задан линейный порядок. То есть при использовании данный типа [math]\mathbf[/math] или [math]\mathbf[/math] имеет смысл переходить к дереву поиска, а при использовании каких-нибудь ссылок на объекты не имеет, так как они не реализуют нужный интерфейс. Такой подход позволяет улучшить производительность с [math]O(n)[/math] до [math]O(\log(n))[/math] . Данный способ используется в таких коллекциях как HashMap, LinkedHashMap и ConcurrentHashMap.

Источник