Способы активации молекул аррениус
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
2.1.9 Влияние температуры на константу скорости реакции
Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:
При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.
Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом:
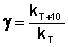
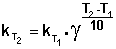
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).
2.1.10 Уравнение Аррениуса
Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.
Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.
Рассмотрим путь некоторой элементарной реакции
Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:
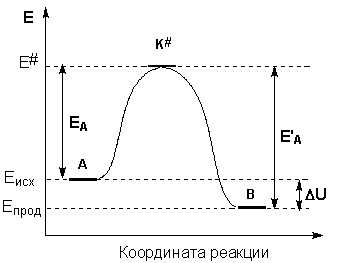
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’А выше, нежели энергия активации прямой реакции EA. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).
Рис. 2.5 Энергетическая диаграмма химической реакции.
Eисх – средняя энергия частиц исходных веществ,
Eпрод – средняя энергия частиц продуктов реакции
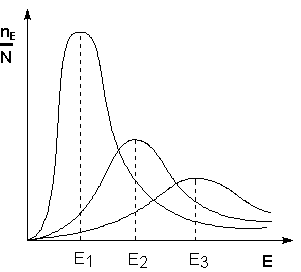
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):
Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
Ei — средняя энергия частиц при температуре Ti (T1 уравнения Аррениуса . Согласно уравнению изобары Вант-Гоффа,
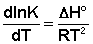
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:
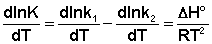
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем:
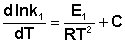
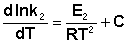
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации :
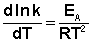
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:
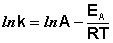
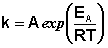
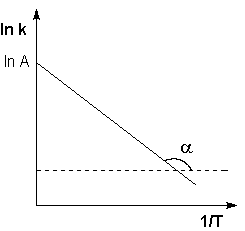
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.
Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации EA и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).
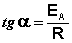
Зная энергию активации реакции и константу скорости при какой-либо температуре T1, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T2:
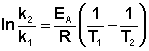
Copyright © С. И. Левченков, 1996 — 2005.
Источник
Теория активизации молекул. Уравнение Аррениуса



Скорость любой химической реакции зависит от числа столкновений реагирующих молекул, так как число столкновения пропорционально концентрациям реагирующих веществ. Однако не все столкновения молекул приводят к акту их взаимодействия, а повышение температуры на 10 0 С приводит к увеличению скорости в 2-4 раза, в то время как число столкновений увеличивается всего на 2 %.
Очевидно, что скорость реакции зависит не только от числа столкновений, но и от каких-то свойств сталкивающихся молекул. Это явление находит объяснение в теории активации С. Аррениуса(1889). Согласно этой теории, реакционноспособны только те молекулы, которые обладают запасом энергии, необходимым для осуществления той или иной реакции, то есть, избыточной энергией по сравнению со средней величиной энергии молекул. Такие молекулы получили название «активных»молекул. Переход неактивной молекулы в активную называется активацией. А избыточная энергия активной молекулы, благодаря которой становится возможной химическая реакция, носит название энергии активации (Ea). Единица измерения Ea Дж/моль или кДж/моль. Энергия активации бывает меньше энергии разрыва связей в молекуле, так как для того чтобы молекула прореагировала, вовсе не требуется полного разрыва связей, их достаточно лишь ослабить.
Величина энергии активации зависит от того, в какую реакцию эта молекула вступает. Иными словами, каждая химическая реакция характеризуется свойственной ей величиной энергии активации. Если реакция идет между атомами или свободными радикалами, то обычно она не превышает 40 кДж/моль, а если между молекулами, то – 150-250 кДж/моль, в полимерах она может достигать 400 кДж/моль. Если Ea выше наибольшей величины, то такая реакция невозможна.
Энергия активации молекул может быть снижена под воздействием внешних факторов: повышение температуры, лучистой энергии, катализаторов и др. Энергия активации проявляется в активных молекулах по-разному: активные молекулы могут обладать большей скоростью движения, повышенной энергией колебания атомов в молекуле и др.
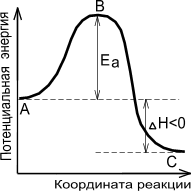
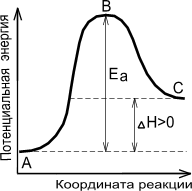
На рис. 7 показано, что скорость реакции пропорциональна числу активных молекул и зависит от величины энергии активации. На этом рисунке по оси ординат отложена энергия рассматриваемой системы молекул, а на оси абсцисс – ход реакции. Если реакция перехода из состояния А в состояние С идет с выделением тепла (экзотермическая реакция), то общий запас энергии продуктов реакции будет меньше, чем исходных веществ. Причем разность энергетических уровней А и С будет равна тепловому эффекту реакции (DН). Энергетический уровень В характеризует то наименьшее количество энергии, которым должны обладать молекулы, чтобы при столкновении друг с другом они прореагировали. Разность между уровнем В и уровнем А характеризует энергию активации прямой реакции, разность между уровнями В и С – энергию активации обратной реакции. Для эндотермической реакции применимы те же рассуждения, но величина энергии активации будет выше, чем у экзотермической реакции. Таким образом, при переходе из состояния А в состояние С система должна преодолеть энергетический барьер, то есть, должна обладать определенным избытком энергии, чтобы вступить в химическое взаимодействие.
Следовательно, скорость химической реакции зависит от величины энергии активации: чем она больше, тем медленнее будет протекать данная реакция. С другой стороны, чем меньше энергетический барьер реакции, тем большее число молекул будет обладать необходимой избыточной энергией, и тем быстрее будет протекать эта реакция. Итак, скорость химической реакции в конечном итоге зависит от соотношения между числом активных и неактивных молекул
В теории активных соударений Аррениус показал, что количество активных молекул может быть вычислено по закону Максвелла-Больцмана:
где Nакт – число активных молекул;
Nобщ – общее число молекул;
e – основание натуральных логарифмов;
Eа – энергия активации, моль/Дж;
R – молярная газовая постоянная, Дж/(мольК);
T – абсолютная термодинамическая температура, К.
Уравнению (5.27) можно придать вид:
k = kоe – E а/ RT (5.28)

или после логарифмирования:
lnk = lnkо – 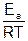
где k – константа скорости при обычных условиях;
kо – константа скорости при условии, что все столкновения приводят к реакции.
 |  |
| Экзотермическая реакция | Эндотермическая реакция |
Рис. 7. Энергетическая диаграмма химической реакции: уровень
А – исходные реагенты, уровень В – активированный комплекс (переходное состояние), уровень С – продукты реакции.
Сравнение уравнений (5.7) и (5.29) позволяет выяснить физический смысл констант в уравнении Аррениуса. A = Eа/RT характеризует энергию активации процессов (Eа), а B = lnkо, т. е. равно логарифму числа столкновений за 1 с в единице объема.
Если известны константы скорости k1 и k2 при двух температурах T1 и T2, то можно найти значение Eа из уравнения (5.29):
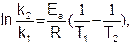
или, заменяя натуральный логарифм десятичным, можно записать:
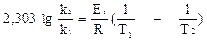
Таким образом, рост скорости реакции с повышением температуры объясняется тем, что с увеличением температуры увеличивается не только средняя кинетическая энергия молекул, но и одновременно, как следует из уравнения (5.7), резко возрастает доля молекул, обладающих энергией выше определенного уровня, то есть, доля активных молекул, способных к реакции.
Источник
Теория активизации молекул. Уравнение Аррениуса
Скорость любой химической реакции зависит от числа столкновений реагирующих молекул, так как число столкновения пропорционально концентрациям реагирующих веществ. Однако не все столкновения молекул приводят к акту их взаимодействия, а повышение температуры на 10 0 С приводит к увеличению скорости в 2-4 раза, в то время как число столкновений увеличивается всего на 2 %.
Очевидно, что скорость реакции зависит не только от числа столкновений, но и от каких-то свойств сталкивающихся молекул. Это явление находит объяснение в теории активации С. Аррениуса(1889). Согласно этой теории, реакционноспособны только те молекулы, которые обладают запасом энергии, необходимым для осуществления той или иной реакции, то есть, избыточной энергией по сравнению со средней величиной энергии молекул. Такие молекулы получили название «активных»молекул. Переход неактивной молекулы в активную называется активацией. А избыточная энергия активной молекулы, благодаря которой становится возможной химическая реакция, носит название энергии активации (Ea). Единица измерения Ea Дж/моль или кДж/моль. Энергия активации бывает меньше энергии разрыва связей в молекуле, так как для того чтобы молекула прореагировала, вовсе не требуется полного разрыва связей, их достаточно лишь ослабить.
Величина энергии активации зависит от того, в какую реакцию эта молекула вступает. Иными словами, каждая химическая реакция характеризуется свойственной ей величиной энергии активации. Если реакция идет между атомами или свободными радикалами, то обычно она не превышает 40 кДж/моль, а если между молекулами, то – 150-250 кДж/моль, в полимерах она может достигать 400 кДж/моль. Если Ea выше наибольшей величины, то такая реакция невозможна.
Энергия активации молекул может быть снижена под воздействием внешних факторов: повышение температуры, лучистой энергии, катализаторов и др. Энергия активации проявляется в активных молекулах по-разному: активные молекулы могут обладать большей скоростью движения, повышенной энергией колебания атомов в молекуле и др.
На рис. 7 показано, что скорость реакции пропорциональна числу активных молекул и зависит от величины энергии активации. На этом рисунке по оси ординат отложена энергия рассматриваемой системы молекул, а на оси абсцисс – ход реакции. Если реакция перехода из состояния А в состояние С идет с выделением тепла (экзотермическая реакция), то общий запас энергии продуктов реакции будет меньше, чем исходных веществ. Причем разность энергетических уровней А и С будет равна тепловому эффекту реакции (DН). Энергетический уровень В характеризует то наименьшее количество энергии, которым должны обладать молекулы, чтобы при столкновении друг с другом они прореагировали. Разность между уровнем В и уровнем А характеризует энергию активации прямой реакции, разность между уровнями В и С – энергию активации обратной реакции. Для эндотермической реакции применимы те же рассуждения, но величина энергии активации будет выше, чем у экзотермической реакции. Таким образом, при переходе из состояния А в состояние С система должна преодолеть энергетический барьер, то есть, должна обладать определенным избытком энергии, чтобы вступить в химическое взаимодействие.
Следовательно, скорость химической реакции зависит от величины энергии активации: чем она больше, тем медленнее будет протекать данная реакция. С другой стороны, чем меньше энергетический барьер реакции, тем большее число молекул будет обладать необходимой избыточной энергией, и тем быстрее будет протекать эта реакция. Итак, скорость химической реакции в конечном итоге зависит от соотношения между числом активных и неактивных молекул
В теории активных соударений Аррениус показал, что количество активных молекул может быть вычислено по закону Максвелла-Больцмана:
где Nакт – число активных молекул;
Nобщ – общее число молекул;
e – основание натуральных логарифмов;
Eа – энергия активации, моль/Дж;
R – молярная газовая постоянная, Дж/(мольК);
T – абсолютная термодинамическая температура, К.
Уравнению (5.27) можно придать вид:
или после логарифмирования:
lnk = lnkо – 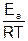
где k – константа скорости при обычных условиях;
kо – константа скорости при условии, что все столкновения приводят к реакции.
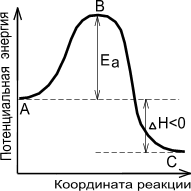 | 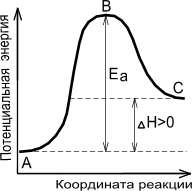 |
| Экзотермическая реакция | Эндотермическая реакция |
Рис. 7. Энергетическая диаграмма химической реакции: уровень
А – исходные реагенты, уровень В – активированный комплекс (переходное состояние), уровень С – продукты реакции.
Сравнение уравнений (5.7) и (5.29) позволяет выяснить физический смысл констант в уравнении Аррениуса. A = Eа/RT характеризует энергию активации процессов (Eа), а B = lnkо, т. е. равно логарифму числа столкновений за 1 с в единице объема.
Если известны константы скорости k1 и k2 при двух температурах T1 и T2, то можно найти значение Eа из уравнения (5.29):
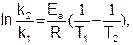
или, заменяя натуральный логарифм десятичным, можно записать:
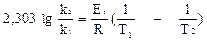
Таким образом, рост скорости реакции с повышением температуры объясняется тем, что с увеличением температуры увеличивается не только средняя кинетическая энергия молекул, но и одновременно, как следует из уравнения (5.7), резко возрастает доля молекул, обладающих энергией выше определенного уровня, то есть, доля активных молекул, способных к реакции.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник