Стабилизация частоты генераторов.



Частота колебаний автогенератора определяется его режимом работы и параметрами контура. В процессе работы генератор подвергается различным воздействиям (изменениям температуры и напряжения, влиянию других усилительных каскадов), вызывающим изменение частоты. Уменьшение влияния этих факторов достигается параметрической и кварцевой стабилизациями.
Параметрическая стабилизация частоты достигается подбором элементов схемы (конденсаторов, катушек индуктивности, резисторов, транзисторов и др.), параметры которых в процессе работы изменяются мало. Температурные влияния уменьшают, применяя термическую герметизацию контуров генераторов в специальных термостатах, используя конденсаторы с отрицательным ТКЕ, компенсирующие увеличение емкости других элементов схемы. Влияние колебаний питающих напряжений снижают, применяя стабилизаторы напряжения и тока. Электромагнитные влияния ослабляют, рационально размещая элементы схемы и экранируя их.
Кварцевая стабилизация является наиболее эффективным способом повышения устойчивости частоты генераторов. Она основана на применении в схемах кварцевых пластинок с сильно выраженным пьезоэлектрическим эффектом. Если к пластине кварца приложить переменное напряжение (поместить ее в электрическое поле ВЧ), то она испытывает периодические механические деформации, т. е. сжимается и разжимается, что в свою очередь вызывает появление электрических зарядов на ее гранях. В результате в цепи (между входными зажимами) течет переменный ток. Этот ток имеет две составляющие IС и IКВ. Реактивный ток IС проходит через емкость, образованную металлическими пластинами кварцедержателя. Ток кварца IКВ обусловлен наличием пьезоэффекта и зависит от частоты приложенного напряжения. Когда частота подведенного переменного напряжения совпадает с собственной частотой механических колебаний кварца, наступает резонанс, при котором амплитуда колебаний будет максимальной. Пьезоэлектрический ток будет наибольшим, а его фаза совпадает с фазой приложенного напряжения. Поэтому вблизи резонансных частот кварцевую пластину можно представить в виде последовательного контура с сосредоточенными постоянными LKCKrK (рис. 22.14, а) и параллельно подключенной к нему статической емкости кварцедержателя С0 (рис. 22.14,б). Практически емкость кварцедержателя С0 в сотни раз больше эквивалентной емкости кварца СК, поэтому собственная резонансная частота кварца как последовательного контура ω1К=1/√LКCК близка к собственной частоте эквивалентного параллельного контура 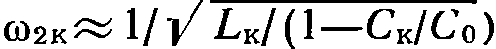
Поскольку С0>>СК, то частота параллельного резонанса ω2К отличается от частоты последовательного резонанса ω1К незначительно. Относительный разнос частот составляет
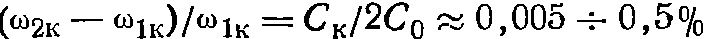
На рис. 22.14, вигизображена зависимость реактивного хКи полного zKсопротивлений кварца от частоты (без учета активных потерь в кварце). Из графиков следует, что при, ω2К > ω> ω1Ксопротивление кварца носит индуктивный, а при ω ω2К—емкостный характер.
Стабильность частоты автоколебаний в зависимости от изменений емкости СК и С0 характеризуется равенствами:
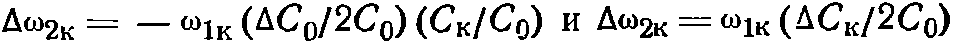
из которых следует, что изменение емкости С0в С0/СК раз меньше влияет на частоту, чем изменение емкости СК.Практически С0/СК≈10 2 -10 4 , поэтому изменение внешней емкости схемы кварцевого автогенератора, подключенной параллельно С0, слабо влияет на частоту автоколебаний.
Добротность кварцевого резонатора на частоте последовательного резонанса
Где 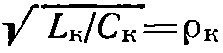
Благодаря большому значению LKи малому СК величины ρК и QK достигают значений, во много раз превышающих их величины в обычных электрических контурах, что обеспечивает малое затухание и очень высокую стабильность резонансной частоты кварцевого контура.
Автоколебания в кварцевом автогенераторе возможны только на частотах вблизи частоты ω1К или ω2К, где сопротивление кварца хКносит индуктивный характер (рис. 22.14, в).На частотах, соответствующих емкостному характеру сопротивления, кварц не возбуждается. Наибольшую добротность имеют кварцы, возбужденные на 5-й — 7-й механических гармониках.

Электрические параметры кварцевого резонатора (частота последовательного ω1К и параллельного ω2К резонансов, добротность QK, температурный коэффициент частоты ТКЧ, предельно допустимая мощность рассеивания РК) определяются геометрическими размерами, типом среза пластин и видом колебаний. Для различных видов среза значение собственной частоты кварца колеблется в пределах f0=l,6/d÷3,6/d (МГц), где d — толщина пластины (мм). Например, для пластины х— среза и колебаний по толщине (вдоль оси_х) собственная частота равна 2,836/d
Рис. 22.14. Схемы и характеристики кварцевых резонаторов
Источник
Лекция 14. Автогенераторы и стабилизация частоты автоколебаний
Лекция 14. АВТОГЕНЕРАТОРЫ И СТАБИЛИЗАЦИЯ
14.1. Назначение, классификация и принцип действия
14.2. Установившийся режим автоколебаний
14.3. Стабильность частоты автогенератора
14.4. Кварцевые автогенераторы
14.5. Контрольные вопросы
14.1. Назначение, классификация и принцип действия
Назначение автогенератора (АГ) состоит в генерации ВЧ колебаний. В АГ происходит преобразование энергии источника постоянного тока в энергию ВЧ колебаний. АГ входит в радиопередающее и радиоприемное устройства.
В зависимости от диапазона частот АГ делятся на две группы: ВЧ и СВЧ. Граница между ними составляет 300 МГц. Различительным признаком может являться не само значение частоты генерируемых колебаний, а тип используемых электрических цепей. В ВЧ генераторах используются цепи с сосредоточенными, а в СВЧ — с распределенными параметрами.
Способы стабилизации частоты автоколебаний:
· параметрическая с использованием обычных колебательных систем;
· кварцевая с использованием в качестве резонатора кристалла кварца;
· с диэлектрическим резонатором (только в СВЧ диапазоне);
· молекулярная за счет индуцированного возбуждения атомов.
По типу электронного прибора и схеме различают два типа АГ:
· с применением электронного прибора с положительной обратной связи,
· с применением генераторного диода (туннельного, лавинно-пролетного или диода Ганна).
По взаимодействию с другими звеньями аппаратуры различают АГ — действующие в автономном режиме, в режиме синхронизации частоты внешним сигналом и в составе устройства автоматической подстройки частоты.
По использованию в составе радиотехнического устройства возможно следующее разделение АГ:
· опорные, с повышенной стабильностью частоты, синхронизирующие работу всех звеньев и каскадов устройства;
· диапазонные, перестраиваемые по частоте, в том числе и в составе синтезатора частот.
Работу АГ характеризуют следующие параметры: диапазон частот, мощность автоколебаний в нагрузке, нестабильность частоты.
Возможны два типа построения АГ с колебательной системой.
В АГ первого типа используется электронный прибор, представляемый в виде нелинейного генератора тока i(uy), где uy — управляющее напряжение (рис. 14.1, а). За счет цепи обратной связи часть мощности сигнала из колебательной системы поступает на вход электронного прибора. После усиления поступившие колебания возвращаются в колебательную систему, компенсируя потери и поддерживая устойчивый режим автоколебаний. При этом необходимо соблюдение условия синхронизма, состоящее в равенстве фаз колебаний, отобранных из колебательной системы и вновь туда поступивших.
 Рис. 14.1. Схема АГ первого типа (с обратной связью).
Рис. 14.1. Схема АГ первого типа (с обратной связью).
Основой второго типа АГ являются специальные генераторные диоды, в эквивалентной схеме которых имеется отрицательная активная проводимость (например, по причине падающего участка в ВАХ или запаздывания сигнала в приборе). Такой прибор при подключении к колебательной системе компенсирует в ней потери, благодаря чему поддерживается режим автоколебаний (рис. 14.1, б).
14.2. Установившийся режим автоколебаний
После включения АГ в нем начинается переходный процесс, в течение которого амплитуда автоколебаний возрастает от 0 до некоторого значения Um. По окончании переходного процесса, длящегося tпер, устройство переходит в режим установившихся автоколебаний (рис. 14.2). Время tпер можно найти, составив и решив нелинейное дифференциальное уравнение, описывающее работу АГ.
Рис. 14.2. Установление автоколебаний в АГ.
В тех случаях, когда отсутствует необходимость определения tпер, можно ограничиться исследованием только установившегося режима работы. Для такого анализа удобен метод гармонического баланса.
Ток электронного прибора i(t) в АГ может существенно отличаться от синусоидального вида и представлять собой периодическое колебание, состоящее из косинусоидальных или иной более сложной формы импульсов. Разложив периодическое колебание в ряд Фурье, выделим из него 1-ю гармонику сигнала, для которой запишем: I1=Imα1, где 1т — амплитуда импульса.
Введем параметр — крутизну характеристики электронного прибора по 1-й гармонике сигнала:
где Uy — амплитуда напряжения на входе прибора, и запишем систему уравнений для комплексных амплитуд 1-й гармоники сигнала:



где Um — амплитуда гармонического напряжения на контуре (ранее было принято, что колебательная система фильтрует все гармоники, кроме 1-й); 

Совместное решение (14.1) дает основное уравнение АГ в комплексной форме по 1-й гармонике сигнала:
Это уравнение распадается на уравнения для произведения модулей и суммы фаз, соответственно называемые уравнениями баланса амплитуд и фаз:


Уравнение баланса амплитуд (14.3) указывает на необходимость пополнения энергии в контур за счет цепи обратной связи, которое покрывало бы потери в нем, а уравнение баланса фаз (14.4) — на соблюдение условия фазировки: дополнительные колебания, вводимые в контур, должны совпадать по фазе с уже существующими.

Рис. 14.3. Трехточечная схема АГ.
Первая из схем (рис. 14.3, а) называется емкостной, в ней модуль К=С1/С2, вторая (рис. 14.3, 6) — индуктивной, в ней модуль К=L2/L1.
Обе схемы могут рассматриваться как эквивалентные по отношению и к двухконтурной (рис. 14.3, в) и к иным схемам автогенератора.
С помощью уравнений (14.3) можно определить амплитуду автоколебаний в установившемся режиме, для чего представим систему (14.1) в виде двух уравнений:
Их совместное решение позволяет найти амплитуды тока 11 и напряжения: Um=I1Rm в установившемся режиме. Графическое решение уравнений приведено на рис 14.4. Для существования устойчивого режима автоколебаний необходима одна точка А пересечения графиков.
Рис. 10.4. Графическое решение уравнений.
Согласно общей теории устойчивости стационарный режим АГ является устойчивым, если малые отклонения амплитуды относительно установившегося значения возвращают систему в первоначальное состояние. Пусть колебания синусоидальны и определяются выражением: u(t)=Uyстeα(U)tcosωt. Тогда согласно сформулированному условию устойчивости следует иметь α(U)=0 при U=Uуст, α(U) Uуст, α(U)>0 при U
Источник




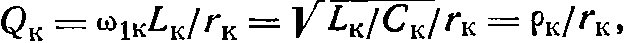
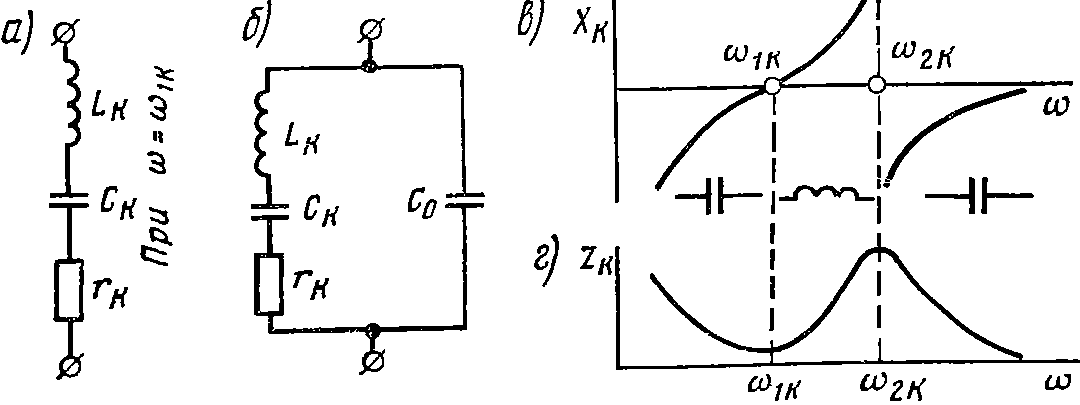

 Рис. 14.1. Схема АГ первого типа (с обратной связью).
Рис. 14.1. Схема АГ первого типа (с обратной связью).




