Способом замены плоскостей проекций определить расстояние между двумя скрещивающимися прямыми

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

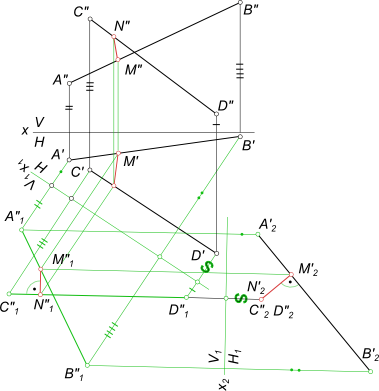
Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Использование метода замены при решении задач

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Источник

Расстояние между скрещивающимися прямыми

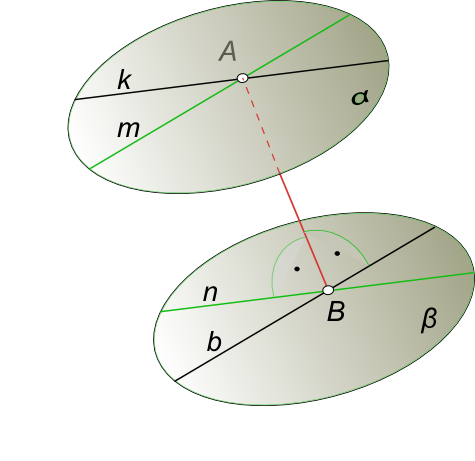
Кратчайшее расстояние между скрещивающимися прямыми определяется величиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые. Эти плоскости называют плоскостями параллелизма.

Для того чтобы через скрещивающиеся прямые k и b провести взаимно параллельные плоскости α и β, достаточно через точку A (A ∈ k) провести прямую m, параллельную прямой b, а через точку B (B ∈ b) прямую n, параллельную прямой k.

Пересекающиеся прямые k и m, b и n определяют взаимно параллельные плоскости α и β. Расстояние между плоскостями α и β равно искомому расстоянию между скрещивающимися прямыми k и b.

В качестве примера решаем задачу на кратчайшее расстояние между скрещивающимися прямыми

способом перемены плоскостей проекций. Здесь они заданны отрезками [AB] и [CD]. Кратчайшее расстояние между скрещивающимися прямыми способом прямоугольного треугольника

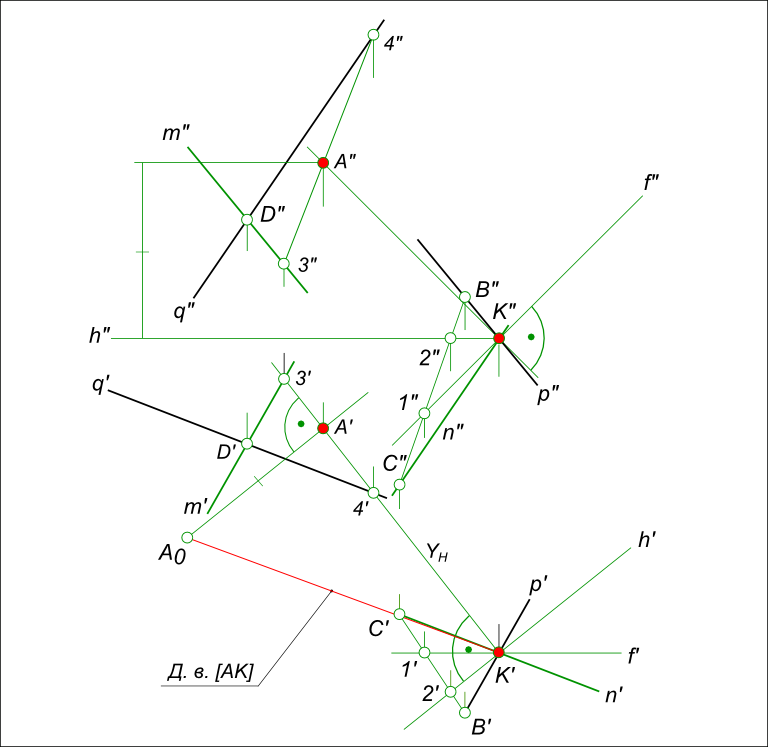
Здесь скрещивающиеся прямые q и p — через произвольно взятые точки D и K на скрещивающихся прямых q и p проводим прямые m║p и n║q. Таким образом, получаем две параллельные плоскости, каждая из пересекающихся прямых, параллельных друг другу; — через точку K восстанавливаем перпендикуляр к плоскости из пересекающихся прямых p и n, для этого: — построим точки C на прямой n и B на прямой p, соединив которые получим треугольный отсек плоскости CBK; — проводим главные линии плоскости CBK горизонталь h и фронталь f; — находим точку пересечения перпендикуляра и плоскости пересекающихся прямых q и m: — заключаем перпендикуляр в горизонтально проецирующую плоскость γ_H; — строим линию пересечения 3 — 4 γ_H и плоскости пересекающихся прямых q и m; — на пересечении линию пересечения 3 — 4 перпендикуляром находим точку A — точку встречи перпендикуляра опущенного из точки K на плоскость пересекающихся прямых q и m; — используя способ прямоугольного треугольника построим действительную величину перпендикуляра [KA] — кратчайшее расстояние между скрещивающимися прямыми q и p.

Решение задачи на определение угла между скрещивающимися прямыми смотри в статье: Угол между скрещивающимися прямыми.

Источник

Расстояние между скрещивающимися прямыми: определение и примеры нахождения

Статья нацелена на нахождение расстояния между скрещивающимися прямыми методом координат. Будет рассмотрено определение расстояния между этими прямыми, получим алгоритм при помощи которого преобразуем нахождение расстояния между скрещивающимися прямыми. Закрепим тему решением подобных примеров.

Расстояние между скрещивающимися прямыми – определение

Предварительно необходимо доказать теорему, которая определяет связь между заданными скрещивающимися прямыми.

Раздел взаимного расположения прямых в пространстве говорит о том, что если две прямые называют скрещивающимися, если их расположение не в одной плоскости.

Через каждую пару скрещивающихся прямых может проходить плоскость, параллельная данной, причем только одна.

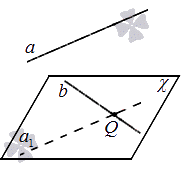
По условию нам даны скрещивающиеся прямые a и b . Необходимо доказать проходимость единственной плоскости через прямую b , параллельную данной прямой a . Аналогичное доказательство необходимо применять для прямой a , через которую проходит плоскость, параллельная данной прямой b .

Для начала необходимо отметить точку Q на прямой b . Если следовать из определения параллельности прямых, то получаем, что через точку пространства можно провести прямую, параллельную заданной прямой, причем только одну. Значит, через точку Q проходит только одна прямая, параллельная прямой a . Примем обозначение а а 1 .

Раздел способов задания плоскости было говорено о том, что прохождение единственной плоскости возможно через две пересекающиеся прямые. Значит, получаем, что прямые b и а 1 – пересекающиеся прямые, через которые проходит плоскость, обозначаемая χ .

Исходя из признака параллельности прямой с плоскостью, можно сделать вывод, что заданная прямая a параллельна относительно плоскости χ , потому как прямая a параллельна прямой а 1 , расположенной в плоскости χ .

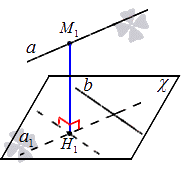
Плоскость χ является единственной, так как прямая, проходящая через заданную прямую, находящуюся в пространстве, параллельна заданной прямой. Рассмотрим на рисунке, предоставленном ниже.

При переходе от определения расстояния между скрещивающимися прямыми определяем расстояние через расстояние между прямой и параллельной ей плоскостью.

Расстоянием между скрещивающимися прямыми называют расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.

То есть расстояние между прямой и плоскостью является расстоянием от заданной точки к плоскости. Тогда применима формулировка определения расстояния между скрещивающимися прямыми.

Расстоянием между скрещивающимися прямыми называют расстояние от некоторой точки скрещивающихся прямых к плоскости, проходящей через другую прямую, параллельную первой прямой.

Произведем подробное рассмотрение прямых a и b . Точка М 1 располагается на прямой a , через прямую b проводится плоскость χ , параллельная прямой a . Из точки М 1 проводим перпендикуляр М 1 Н 1 к плоскости χ . Длина этого перпендикуляра является расстоянием между скрещивающимися прямыми a и b . Рассмотрим на рисунке, приведенном ниже.

Нахождение расстояния между скрещивающимися прямыми – теория, примеры, решения

Расстояния между скрещивающимися прямыми находятся при построении отрезка. Искомое расстояние равняется длине этого отрезка. По условию задачи его длина находится по теореме Пифагора, по признакам равенства или подобия треугольников или другим.

Когда имеем трехмерное пространство с системой координат О х у z с заданными в ней прямыми a и b , то вычисления следует проводить, начиная с расстояния между заданными скрещивающимися при помощи метода координат. Произведем подробное рассмотрение.

Пусть по условию χ является плоскостью, проходящей через прямую b , которая параллельна прямой a . Искомое расстояние между скрещивающимися прямыми a и b равняется расстоянию от точки М 1 , расположенной на прямой a , к плоскости _ χ . Для того, чтобы получить нормальное уравнение плоскости χ , необходимо определить координаты точки M 1 ( x 1 , y 1 , z 1 ) _, расположенной на прямой a . Тогда получим cos α · x + cos β · y + cos γ · z — p = 0 , которое необходимо для определения расстояния M 1 H 1 от точки M 1 x 1 , y 1 , z 1 к плоскости χ . Вычисления производятся по формуле M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p . Необходимое расстояние равняется искомому расстоянию между скрещивающимися прямыми.

Данная задача предполагает получение координат точки М 1 , которая располагается на прямой a , нахождение нормального уравнения плоскости χ .

Определение координат точки М 1 необходимо и возможно при знании основных видов уравнений прямой в пространстве. Чтобы получить уравнение плоскости χ , необходимо остановиться подробней на алгоритме вычисления.

Если координаты x 2 , y 2 , z 2 будут определены при помощи точки М 2 , через которую проведена плоскость χ , получаем нормальный вектор плоскости χ в виде вектора n → = ( A , B , C ) . Следуя из этого, можно записать общее уравнение плоскости χ в виде A · x — x 2 + B · ( y — y 2 ) + C · ( z — z 2 ) = 0 .

Вместо точки М 2 может быть взята любая другая точка, принадлежащая прямой b , потому как плоскость χ проходит через нее. Значит, координаты точки М 2 найдены. Необходимо перейти к нахождению нормального вектора плоскости χ .

Имеем, что плоскость χ проходит через прямую b , причем параллельна прямой a . Значит, нормальный вектор плоскости χ перпендикулярен направляющему вектору прямой a , обозначим a → , и направляющему вектору прямой b , обозначим b → . Вектор n → будет равняться векторному произведению a → и b → , что значит, n → = a → × b → . После определения координат a x , a y , a z и b x , b y , b z направляющих векторов заданных прямых a и b , вычисляем

n → = a → × b → = i → j → k → a x a y a z b x b y b z

Отсюда находим значение координат A , B , C нормального вектора к плоскости χ .

Знаем, что общее уравнение плоскости χ имеет вид A · ( x — x 2 ) + B · ( y — y 2 ) + C · ( z — z 2 ) = 0 .

Необходимо привести уравнение к нормальному виду cos α · x + cos β · y + cos γ · z — p = 0 . После чего нужно произвести вычисления искомого расстояния между скрещивающимися прямыми a и b , исходя из формулы M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p .

Чтобы найти расстояние между скрещивающимися прямыми a и b , необходимо следовать алгоритму:

• определение координат ( x 1 , y 1 , z 1 ) и x 2 , y 2 , z 2 точек М 1 и М 2 , расположенных на прямых a и b соответственно;
• получение координат a x , a y , a z и b x , b y , b z , принадлежащих направляющим векторам прямых a и b ;
• нахождение координат A , B , C , принадлежащих вектору n → на плоскости χ , проходящей через прямую b , расположенную параллельно a , по равенству n → = a → × b → = i → j → k → a x a y a z b x b y b z ;
• запись общего уравнения плоскости χ в виде A · x — x 2 + B · ( y — y 2 ) + C · ( z — z 2 ) = 0 ;
• приведение полученного уравнения плоскости χ к уравнению нормального вида cos α · x + cos β · y + cos γ · z — p = 0 ;
• вычисление расстояния M 1 H 1 от M 1 x 1 , y 1 , z 1 к плоскости χ , исходя из формулы M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p .

Пример 1

Имеются две скрещивающиеся прямые в прямоугольной системе координат О х у z трехмерного пространства. Прямая a определена параметрическим уравнением прямой в пространстве x = — 2 y = 1 + 2 · λ z = 4 — 3 · λ , прямая b при помощи канонического уравнения прямой в пространстве x 1 = y — 1 — 2 = z + 4 6 . Найти расстояние между скрещивающимися прямыми.

Понятно, что прямая а пересекает точку M 1 ( — 2 , 1 , 4 ) с направляющим вектором a → = ( 0 , 2 , — 3 ) , а прямая b пересекает точку M 2 ( 0 , 1 , — 4 ) с направляющим вектором b → = ( 1 , — 2 , 6 ) .

Для начала следует произвести вычисление направляющих векторов a → = ( 0 , 2 , — 3 ) и b → = ( 1 , — 2 , 6 ) по формуле. Тогда получаем, что

a → × b → = i → j → k → 0 2 — 3 1 — 2 6 = 6 · i → — 3 · j → — 2 · k →

Отсюда получаем, что n → = a → × b → — это вектор плоскости χ , который проходит через прямую b параллельно a с координатами 6 , — 3 , — 2 . Получим:

6 · ( x — 0 ) — 3 · ( y — 1 ) — 2 · ( z — ( — 4 ) ) = 0 ⇔ 6 x — 3 y — 2 z — 5 = 0

Находим нормирующий множитель для общего уравнения плоскости 6 x — 3 y — 2 z — 5 = 0 . Вычислим по формуле 1 6 2 + — 3 2 + — 2 2 = 1 7 . Значит, нормальное уравнение примет вид 6 7 x — 3 7 y — 2 7 z — 5 7 = 0 .

Необходимо воспользоваться формулой, чтобы найти расстояние от точки M 1 — 2 , 1 , 4 до плоскости, заданной уравнением 6 7 x — 3 7 y — 2 7 z — 5 7 = 0 . Получаем, что

M 1 H 1 = 6 7 · ( — 2 ) — 3 7 · 1 — 2 7 · 4 — 5 7 = — 28 7 = 4

Отсюда следует, что искомым расстоянием является расстояние между заданными скрещивающимися прямыми, является значение 4 .

Источник