Способом замены плоскостей проекций определить натуральную величину высоты пирамиды sabc

Содержание

Определить натуральную величину высоты пирамиды
Метод замены плоскостей проекций
Натуральная величина перпендикуляра
Решение задачи способом замены плоскостей проекций.
Определить натуральную величину высоты SO пирамиды SABC
Замена плоскостей
Построение перпендикуляра
Способом замены плоскостей проекций определить натуральную величину высоты пирамиды sabc
58. Способ замены плоскостей проекций

Определить натуральную величину высоты пирамиды

Задача определения натуральной величины высоты пирамиды соответствует задаче определения расстояния от точки до плоскости. Решение задачи в начертательной геометрии возможно двумя методами: (1) заменой плоскостей проекций перевести плоскость основания пирамиды в проецирующее положение и (2) опустить перпендикуляр из вершины на плоскость основания, найти пересечение прямой перпендикуляра с плоскостью и определить натуральную величину отрезка прямой от вершины пирамиды до точки пересечения с основанием.

Метод замены плоскостей проекций

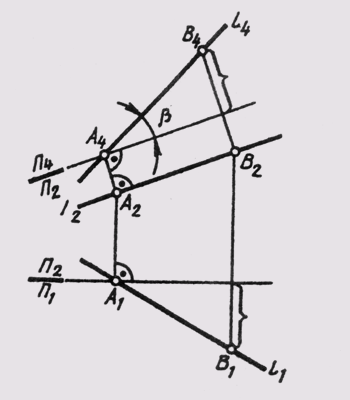
В плоскости основания пирамиды проводится линия частного положения (в примере — горизонталь BH). Строится плоскость проекции заменяющая одну из исходных плоскостей (в примере П₄ заменяет фронтальную проекцию). На новой проекции, плоскость основания занимает проецирующее положение и расстояние от любой точки до этой плоскости очевидно представляется перпендикуляром. В примере, h — высота пирамиды проведённая из вершины к основанию. Так как h параллелен плоскости проекций, то его длинна определяет натуральную величину высоты пирамиды.

Натуральная величина перпендикуляра

В плоскости основания определены горизонталь и фронталь. Из вершины пирамиды проводится перпендикуляр к основанию. Через перпендикуляр проведена горизонтально проецирующая плоскость-посредник пересекающая основание по 12. На фронтальной проекции пересечение 1₂2₂ и перпендикуляра даёт общую точку для перпендикуляра и 12, которая лежит в плоскости основания. Следовательно, эта точка пересечения N определяет точку пересечения перпендикуляра и основания. Натуральная величина перпендикуляра AN определена методом прямоугольного треугольника: фронтальная проекция AN использована как катет-основание прямоугольного треугольника, второй катет определен как растояние между концами перпендикуляра измеренное вдоль оси Y. Гипотенуза полученного треугольника определяет натуральную величину высоты пирамиды.

Источник

Решение задачи способом замены плоскостей проекций.

Как отмечалось выше, для определения расстояния от заданной точки до плоскости (высоты пирамиды) необходимо из этой точки опустить перпендикуляр на плоскость, найти основание перпендикуляра и определить истинную величину отрезка. Задача решается просто, если плоскости основания пирамиды — ΔАВС задать проецирующее положение.

1. Построим в плоскости треугольника АВС горизонталь и введем новую фронтальную плоскость π₄ перпендикулярно к данной горизонтали:

На чертеже ось х₁ перпендикулярна горизонтальной проекции горизонтали h₁ / : х₁ ^ h₁ / ; (рис.10.1)

2.Строим новую фронтальную проекцию треугольника — А₁ // В₁ // С₁ // .

[S // S_x // ] [S₁ // S_x1 // ]; [A // A_x // ] [A₁ // A_x1 // ]; [B // B_x // ] [B₁ // B_x1 // ];

[C // C_x // ] [C₁ // C_x₁ // ];

По отношению к p₄ плоскость треугольника занимает проецирующее положение(рис.10.2).

3. Из точки S₁опускаем перпендикуляр на плоскость DА₁В₁С₁, находим его основание, как точку пересечения перпендикуляра с плоскостью:

S₁K₁ 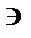S_1; S₁K₁ DА₁В₁С₁ ; S₁K₁∩DА₁В₁С₁ =K₁;

На чертеже: S₁«K₁» DA₁ // В₁ // C₁ // ;

Отрезок [S₁«K₁«]определяет натуральную величину высоты пирамиды. Измеряем его и указываем размер на чертеже.

Точку К необходимо вернуть в исходное положение, зная что S₁ / K / ¤¤ х (рис.10.3);

Задача 3. Определить натуральную величину основания пирамиды — DАВС.

Решение способом плоскопараллельного перемещения.

Для того чтобы определить натуральную величину основания пирамиды-DABC, который является плоскостью общего положения, необходимо преобразовать его в плоскость уровня.

Для решения задачи необходимо выполнить два преобразования:

1) Преобразовать плоскость треугольника – плоскость общего положения в проецирующую плоскость.

2) Преобразовать проецирующую плоскость в плоскость уровня,

переместив ΔA₁B₁C₁ плоскопараллельным движением относительно пл. p₂ в новое положение, параллельное пл. p₁, тогда на эту плоскость он спроецируется без искажения.

Читайте также: Процесс бессемеровского способа производства стали
a₁(A₁B₁C₁) 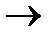a₂(A₂B₂C₂)// p₁ ;

1. Перемещаем треугольник АВС параллельно одной из плоскостей проекций так, чтобы после преобразования он занял проецирующее положение ( см. задачу №1).

2.Располагаем вырожденную фронтальную проекцию DA₂B₂C₂ –отрезок [A₂ // B₂ // C₂ // ]параллельно оси х:

При этом не изменится величина его фронтальной проекции:

[A₂ // B₂ // C₂ // ] [A₁ // B₁ // C₁ // ] (рис.11.1)

3. Горизонтальные проекции вершин А₁ / , В₁ / , . перемещаются в новое положение А₂ / ,В₂ / , . по прямым параллельным оси х. По линиям связи строим горизонтальную проекцию DA₂B₂C₂ (ΔA₂ / B₂ C₂ / ), которая конгруэнтна основанию пирамиды: [DA₂ / B₂ / C₂ / ] [DABC] (рис.11.2)

Источник

Определить натуральную величину высоты SO пирамиды SABC

Определить натуральную величину высоты SO пирамиды SABC можно методом замены плоскостей для получения проецирующего положения основания или непосредственное построение в исходных проекция перпендикуляра к основанию.

Замена плоскостей

В плоскости основания пирамиды определена фронталь. Перпендикулярно фронтали построена П₄ плоскость заменяющая горизонтальную проекцию пирамиды SABC. На П₄ плоскость основания пирамиды SABC занимает проецирующее положение и любой перпендикулярный отрезок равен натуральной величине, в т.ч. и высота SO.

Фронтальная проекция высоты SO построена из условия принадлежности точки основания перпендикуляру, а перпендикуляр определен по условию проецирования прямого угла в натуральную величину.

Построение перпендикуляра

В плоскости основания пирамиды SABC определены горизонталь и фронталь. Из вершины пирамиды проведён перпендикуляр высоты к плоскости основания. Горизонтальная проекция перпендикуляра высоты перпендикулярен горизонтальной проекции горизонтали, фронтальная — фронтали.

Для определения пересечения перпендикуляра высоты с основанием пирамиды SABC использован метод плоскости посредника. Через перпендикуляр проведена горизонтально проецирующая плоскость, которая пересекает основание пирамиды SABC по прямой 12. Пересечение фронтальной проекции 12 и перпендикуляра определяют общую точку (пересечение) высоты и основания пирамиды SABC (т.к. 12 и высота лежат в одной плоскости посреднике, а 12 лежит в основании).

Натуральная величина высоты SO пирамиды SABC определена методом прямоугольного треугольника.

Источник

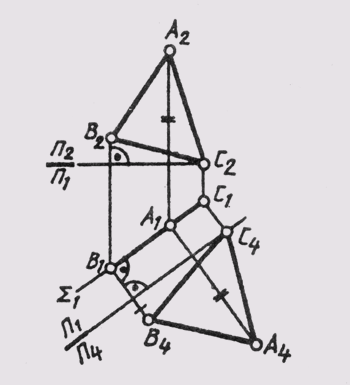
Способом замены плоскостей проекций определить натуральную величину высоты пирамиды sabc

1) Соединяешь все точки в линии, те которые не видимы пунктиром.
2) Проводишь горизонталь, сверху и снизу
3) Проводишь фронталь, сверху и снизу
4) Из точки S2 перпендикулярно фронтали проводишь прямую L2
5) Из точки S1 перпендикулярно горизонтали проводишь прямую L1
6) Точка пересечения линии A2C2 — 3(2) проецируешь и получаешь 3(1)
7) Точка пересечения линии В2C2 — 4(2) проецируешь и получаешь 4(1)
8) Пересечение линии 3(1)-4(1) с прямой L1 получаешь точку D1
9) Проецируешь D2
10) Строишь разность высот с точками A2-D2 и S2-D2
11) От линии A1-D1 проводишь перпендикуляр из точки A1 на расстояние разницы высот A2-D2. Соединяешь их в треугольник, гипотенуза = H.B.[AD]
12) От линии S1-D1 проводишь перпендикуляр из точки S1 на расстояние разницы высот S2-D2. Соединяешь их в треугольник, гипотенуза = H.B.[SD]
13) В левом нижнем углу берём точку, обзываем её D, из неё строим под прямым углом (то есть перпендикулярно друг к другу) две линии:
вверх, линию, равную по размерам H.B.[SD], самую верхнюю точку данной линии обзываем S,
вниз, линию, равную по размерам H.B.[AD], самую правую точку данной линии обываем A,
Соединяем эти две точки (S и A), получаем треугольник.
Если данный треугольник в самом левом нижнем углу не помещается в связи со своими размерами, то разрешается его запихнуть, куда-нибудь в другое место, но желательно внизу чертежа.

Строим изометрию:
Рисуем одну вертикальную линию — Z ось.
От нижней точки оси Z под с помощью угольника откладываем 60 градусов в правую сторону и получаем ось Y, переворачиваем угольник и строим ось влево, получаем ось X. Таким образом, каждая ось находится друг от друга под 120 градусов.
Теперь но оси X откладываем точки A, B, C, S и D (то есть по иксу). Берём инженерную линейку, она же Рейсшина, проводим относительно оси Y параллель из точек A, B, C, S и D, на соответствующее им расстояние по Y. Расстояние для откладывания берём из чертежа и задания на РГР. Полученные точки обзываем A1′ B1′ C1′ S1′ и D1′.
Берём ещё раз рейсшину и параллельно вертикальной оси Z откладываем на соответственное расстояние точки вверх от точек A1′ B1′ C1′ S1′ и D1′. Обзываем полученные точки A’ B’ C’ S’ и D’.
Соединяем точки в линиях:
A1′-B1′ A1′-C1′ B1′- C1′ A1′-S1′ B1′-S1′ C1′-S1′
D1′-S1′
A’-B’ A’-C’ B’- C’ A’-S’ B’-S’ C’-S’
D’-S’
Диметрия строится так же, только угол у нею будет не 120 градусов всех линий друг к другу.

Читайте также: Методика обучения плаванию способом брассом
Надписи:
Все надписи делать 7 шрифтом. Разрешается от руки, приближенного к ГОСТ.
В правом, верхнем углу записываем координаты точек A, B, C, S по осям X, Y, Z. Если не помещается прямоугольником вниз, можно развернуть прямоугольником вправо.
Затем, над чертежом Изометрии/Диметрии записываете задание НАКЛОННЫМ шрифтом:
«Построить проекции и определить натуральную величину высоты SD пирамиды и угла наклона ребра AS к основанию ABC. Построить аксонометрическую проекцию пирамиды и ее высоты». Переносы допускаются.

Источник

58. Способ замены плоскостей проекций

Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.

Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.

Рассмотрим решение четырех исходных задач способом замены плоскостей проекций.

1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.

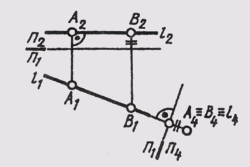
Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П₄, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П₁_|_П₂ перейти к системе П₄ _|_ П₁ или П₄ _|_ П₂. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П₁ _|_ П₄, причем П₄ || l. Новые линии связи A₁A₄ и В₁В₄проведены

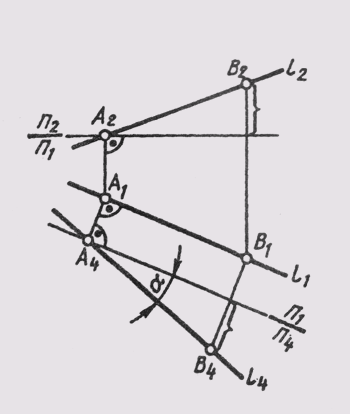
перпендикулярно новой оси —П₁/П₄ параллельной горизонтальной проекции l₁.

Новая проекция прямой дает истинную величину А₄В₄отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций (а = L₁П₁). Угол наклона прямой к фронтальной плоскости проекций (b = L₁П₂) можно определить, построив изображение прямой на другой дополнительной плоскости П4_|_П₂ (рис. 109).

2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.

Чтобы на новой плоскости проекций изображение прямой было точкой (см. § 10), новую плоскость проекций нужно расположить перпендикулярно данной прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П₄_|_ П₁. (рис. 110), а фронталь f— на П₄_|_ П₂

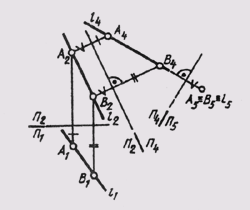
Читайте также: Каким способом можно получить индукционный ток
Если требуется построить вырожденную в точку проекцию прямой общего положения, то для преобразования чертежа потребуется произвести две последовательные замены плоскостей проекций. На рис. 111 исходный чертеж прямой l (А,В) преобразован следующим образом: сначала построено изображение прямой на плоскости П₄_|_ П₂, расположенной параллельно самой прямой l. В системе плоскостей П₂_|_ П₄, прямая заняла положение линии l уровня (А₂А₄ _|_П₂/П₁;

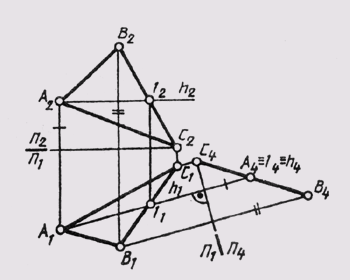
П₄ _|_П₅, причем вторая новая плоскость проекций П₅ перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П₄, то на плоскости П₅ получаем изображение прямой в виде точки (А₅ = B₅ = l₅).

3. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение.

Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из основных плоскостей проекций. Это возможно сделать, если учесть, что направление ортогонального проецирования на новую плоскость проекций должно совпадать с направлением соответствующих линий уровня данной плоскости общего положения. Тогда все линии этого уровня на новой плоскости проекций изобразятся точками, которые и дадут «вырожденную» в прямую проекцию плоскости (см. § 47).

На рис. 112 дано построение нового изображения плоскости 0 (ABC) в системе плоскостей П₄ _|_П₁. Для этого в плоскости 0 построена горизонталь h(A, 1), и новая плоскость проекций П₄ расположена перпендикулярно горизонтали h. Графическое решение третьей исходной задачи приводят к построению изображения плоскости в виде прямой линии, угол наклона которой к новой оси проекции П₁/П₄, определяет угол наклона а плоскости Q(ABC) к горизонтальной плоскости проекций (а = Q ^ П₁).

Построив изображение плоскости общего положения в системе П₂ _|_П₄, (П₄ расположить перпендикулярно фронтали плоскости),

можно определить угол наклона Р этой плоскости к фронтальной плоскости проекций.

4. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня.

Решение этой задачи позволяет определить величину плоских фигур.

Новую плоскость проекций нужно расположить параллельно заданной плоскости. Если исходное положение плоскости было фронтально проецирующим, то новое изображение строят в системе и П₂ _|_П₄, а если горизонтально проецирующим, то в системе П₁ _|_П₄. Новая ось проекций будет расположена параллельно вырожденной проекции проецирующей плоскости (см. § 47). На рис. 113 построена новая проекция А₄В₄С₄горизонтально проецирующей плоскости Sum (ABC) на плоскости П₄ _|_П₁

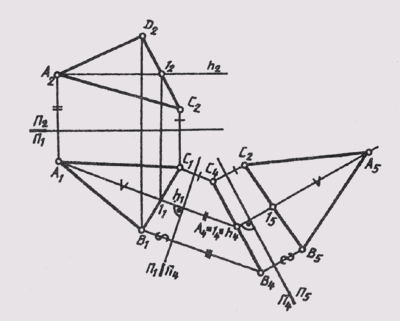
Если в исходном положении плоскость занимает общее положение, а нужно получить изображение ее как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно задачу 3; а затем задачу 4. При первой замене плоскость становится проецирующей, а при второй — плоскостью уровня (рис. 114).

В плоскости А(DEF) проведена горизонталь h (D — 1). По отношению к горизонтали проведена первая ось П₁ / П₄ _|_h₁. Вторая новая ось

проекций параллельна вырожденной проекции плоскости, а новые линии связи — перпендикулярны вырожденной проекции плоскости. Расстояния для построения проекций точек на плоскости П₅ нужно замерить на плоскости П₁от оси П₁ / П₂и откладывать по новым линиям связи от новой оси П₄ /П₅. Проекция D₅E₅F₅треугольника DEF конгруэнтна самому треугольнику ABC.

С применением способа замены плоскостей можно решать ряд других задач как самостоятельных, так и отдельных частей задач, включающих большой объем графических решений.

Источник