Способом замены плоскостей проекций определить кратчайшее расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми

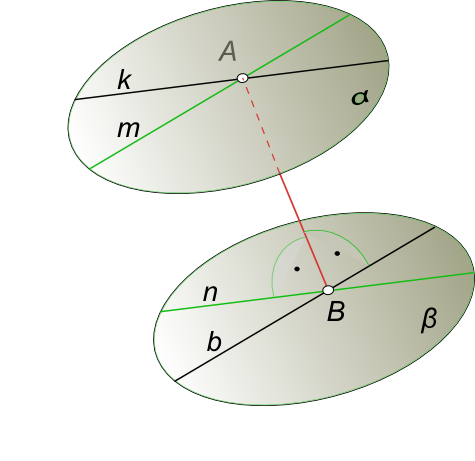
Кратчайшее расстояние между скрещивающимися прямыми определяется величиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые. Эти плоскости называют плоскостями параллелизма.

Для того чтобы через скрещивающиеся прямые k и b провести взаимно параллельные плоскости α и β, достаточно через точку A (A ∈ k) провести прямую m, параллельную прямой b, а через точку B (B ∈ b) прямую n, параллельную прямой k.

Пересекающиеся прямые k и m, b и n определяют взаимно параллельные плоскости α и β. Расстояние между плоскостями α и β равно искомому расстоянию между скрещивающимися прямыми k и b.

В качестве примера решаем задачу на кратчайшее расстояние между скрещивающимися прямыми

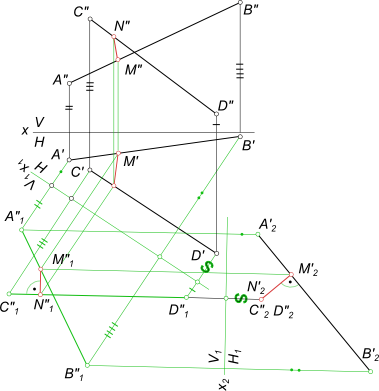
способом перемены плоскостей проекций. Здесь они заданны отрезками [AB] и [CD]. Кратчайшее расстояние между скрещивающимися прямыми способом прямоугольного треугольника

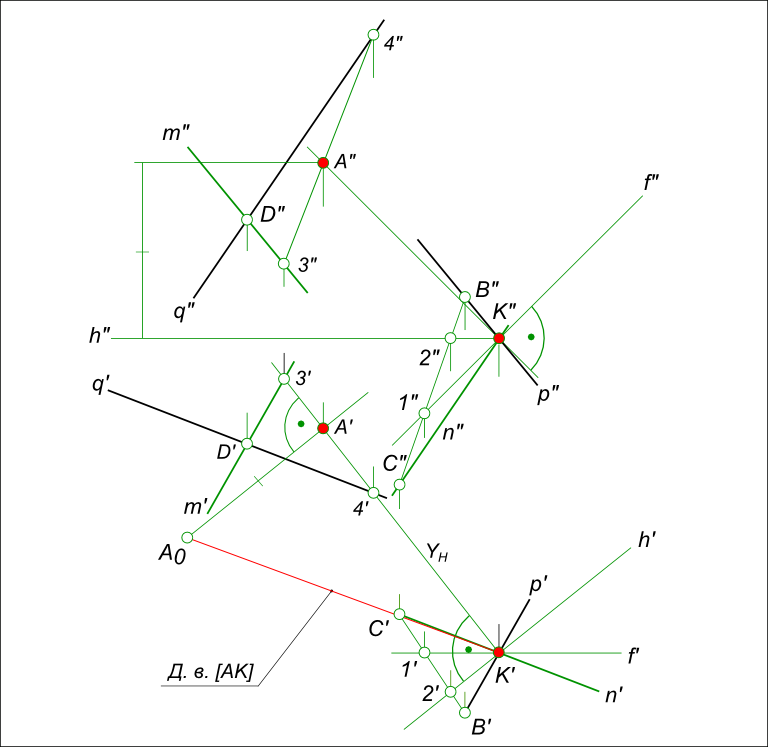
Здесь скрещивающиеся прямые q и p — через произвольно взятые точки D и K на скрещивающихся прямых q и p проводим прямые m║p и n║q. Таким образом, получаем две параллельные плоскости, каждая из пересекающихся прямых, параллельных друг другу; — через точку K восстанавливаем перпендикуляр к плоскости из пересекающихся прямых p и n, для этого: — построим точки C на прямой n и B на прямой p, соединив которые получим треугольный отсек плоскости CBK; — проводим главные линии плоскости CBK горизонталь h и фронталь f; — находим точку пересечения перпендикуляра и плоскости пересекающихся прямых q и m: — заключаем перпендикуляр в горизонтально проецирующую плоскость γ_H; — строим линию пересечения 3 — 4 γ_H и плоскости пересекающихся прямых q и m; — на пересечении линию пересечения 3 — 4 перпендикуляром находим точку A — точку встречи перпендикуляра опущенного из точки K на плоскость пересекающихся прямых q и m; — используя способ прямоугольного треугольника построим действительную величину перпендикуляра [KA] — кратчайшее расстояние между скрещивающимися прямыми q и p.

Решение задачи на определение угла между скрещивающимися прямыми смотри в статье: Угол между скрещивающимися прямыми.

Источник

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Использование метода замены при решении задач

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Источник

Определение расстояния между скрещивающимися прямыми

Приведем без доказательств сведения из стереометрии, необходимые для решения названной задачи.

1. Общим перпендикуляром двух скрещивающихся прямых называется отрезок,

концы которого лежат на данных прямых и который перпендикулярен к ним.

2. Общий перпендикуляр двух скрещивающихся прямых существует и единствен.

3. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.

Задача. Даны скрещивающиеся прямые АВ и CD. Определить расстояние между прямыми (рис. 8.7).

Решение задачи выполним методом замены плоскостей проекций. Проекционный алгоритм решения в этом случае может быть следующим:

1) вводится новая система плоскостей проекций

П₁, П₄ , таким образом, что П₄ // АВ, т.е. на КЧ

2) на П₄ строятся новые проекции А₄В₄ ( НВ отрезка АВ) и C₄D₄ ;

3) вводится новая система плоскостей П₄, П₅ с

4) на П₅ строятся новые проекции – отрезок C₅D₅ и точка А₅ = В₅;

В итоге, по смыслу построений в методе замены плоскостей проекций и приведенному понятию расстояния между скрещивающимися прямыми, получаем, что r(E₅, C₅D₅) = r(AB, CD). Для полноты решения задачи необходимо вернуть отрезок EF длиной r(AB, CD) на исходные плоскости проекций:

Отрезки E₂F₂ , E₁F₁ представляют собой основные проекции отрезка EF.

В стереометрии известно еще одно определение рассматриваемого расстояния: расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведенными через эти прямые.

Такое определение расстояния позволяет предложить более короткий путь решения рассматриваемой задачи. Пусть AB и CD – скрещивающиеся прямые (рис. 8.8). Переместим в пространстве прямую АВ параллельно самой себе в положение А 1 В 1 до пересечения с CD. Если взять теперь на прямой АВ любую точку Е и опустить из этой точки перпендикуляр ЕЕ 1 на образовавшуюся плоскость Σ(CD, A 1 B 1 ), то длина этого перпендикуляра будет искомым расстоянием r(AB,CD). Рассмотрим проекционное решение задачи.

Задача. Даны скрещивающиеся прямые АВ и CD (рис. 8.9). Определить расстояние между ними.

Решение задачи может быть следующим.

1. Перенесем прямую АВ параллельно самой себе до пересечения с CD. Таких

переносов может быть бесконечное множество. Один из переносов, например

2. Получаем новые условия задачи: задана плоскость Σ (А 1 В 1 , CD), где А 1 В 1 Ç CD и точка А; требуется определить расстояние r(А, Σ). Решение задачи выполняется методом замены плоскостей проекций по ранее изложенной схеме проекционного решения.

Определение углов

Между фигурами

Фигуры пространства: прямые линии, плоскости, прямые и плоскости могут образовывать между собой углы – геометрические фигуры с соответствующими этим фигурам величинами. Рассмотрим наиболее часто встречающиеся в начертательной геометрии углы.

Углы между прямыми

Приведем известные из школьного курса стереометрии понятия и определения, необходимые для решения последующих метрических задач:

1) плоский угол – фигура, образованная двумя лучами с общим началом и одной

из плоских областей, ограниченной ими;

2) угол между пересекающимися прямыми – величина наименьшего из плоских

углов, образованных этими прямыми;

3) угол между скрещивающимися прямыми – это угол между пересекающимися

прямыми, параллельными данным скрещивающимся прямым.

В последнем определении величина угла между двумя скрещивающимися прямыми не зависит от выбора пары пересекающихся прямых, параллельных им. Рассмотрим несколько задач на определение углов.

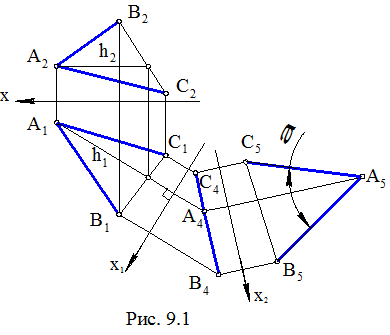
Задача.Даны пересекающиеся отрезки АВ и АС (рис. 9.1). Определить угол между ними.

Поскольку искомый угол является плоской фигурой, то решение задачи сводится к определению НВ плоской фигуры. Ее проекционное решение изложено в п. 1. Напомним алгоритм этого решения. Он основан на методе замены плоскостей проекций и применительно к условиям данной задачи может быть следующим:

1) строится линия уровня, например, h(h₁,h₂), принадлежащая плоскости Σ(АВ, АС), при этом h₂ // х;

2) строится ось проекции x₁^ h₁ , что соответствует введению в пространстве новой системы плоскостей проекций П₁, П₄, где П₄ ^ h;

3) на П₄ строится вырожденная проекция В₄С₄ плоскости Σ;

4) строится ось проекции x₂ // В₄С₄ , что соответствует введению в пространстве

новой системы плоскостей проекций П₄ , П₅ , где П₅ // Σ;

5) на П₅ строится угол Ð(А₅С₅ , А₅В₅ ) = a, который и является искомым.

Задача. Даны две скрещивающиеся прямые АВ и CD (рис. 9.2). Определить угол между ними.

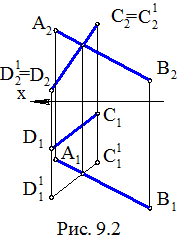
Решение задачи выполним, опираясь на определение угла между скрещивающимися прямыми, приведенное выше, а также учитывая алгоритм проекционного решения предыдущей задачи. Для этих целей переместим одну из прямых, например DC, в положение, когда она, оставаясь параллельной самой себе, будет пересекать другую прямую АВ. Таких положений существует бесчисленное множество. Одно из них, например D 1 C 1 (D₁ 1 C₁ 1 , D₂ 1 C₂ 1 ), где D₁ 1 С₁ 1 // D₁С₁ , D₂ 1 С₂ 1 = D₂C₂ , показано на КЧ (см. рис. 9.2). В итоге получаем пару пересекающихся прямых АВ Ç D 1 С 1 , угол между которыми может быть определен на основании вышеприведенного алгоритма.

Эту часть решения задачи рекомендуется выполнить самостоятельно.

Рассмотрим еще одно проекционное решение данной задачи. Смысл его заключается в построении такой дополнительной плоскости проекций, на которой ортогональные проекции заданных скрещивающихся прямых суть пересекающиеся прямые, соответственно параллельные этим скрещивающимся прямым. Угол между такими ортогональными проекциями является искомым. Указанная плоскость проекций перпендикулярна прямой кратчайшего расстояния между заданными скрещивающимися прямыми.

Задача.Даны скрещивающиеся прямые АВ и CD. Определить угол между ними

Проекционное решение этой задачи, в соответствии с предложенной выше схемой, будет следующим:

1) строится ось проекции x₁ // C₁D₁ (x₁ можно строить параллельно любой из четырех ортогональных проекций прямых АВ и CD), которая вместе с плоскостями П₁ , П₄ образует новую систему плоскостей проекций, такую, что П₄ // CD;

2) на П₄ строятся дополнительные проекции А₄В₄ , C₄D₄ прямых АВ и CD, при этом C₄D₄ есть НВ отрезка CD;

3) строится ось проекции x₂ ^ C₄D₄ , которая вместе с П₄ , П₅ образует новую систему плоскостей проекций, такую, что П₅ ^CD;

4) на П₅ строятся дополнительные проекции А₅В₅ и C₅ = D₅ прямых АВ и CD;

5) строится ось проекции x₃ // А₅В₅ , которая

вместе с П₅, П₆ образует новую систему плоскостей проекций, такую, что П₆ // AB;

6) на П₆ строятся дополнительные проекции

А₆В₆ и C₆D₆ , представляющих собой НВ прямых АВ и CD и образующих между собой угол a, являющийся решением задачи.

Источник