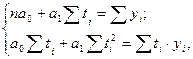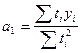Способом выявления тенденции ряда динамики является
7.5 чЩСЧМЕОЙЕ ПУОПЧОПК ФЕОДЕОГЙЙ ТСДБ ДЙОБНЙЛЙ
пДОБ ЙЪ ЧБЦОЕКЫЙИ ЪБДБЮ БОБМЙЪБ ТСДБ ДЙОБНЙЛЙ ЪБЛМАЮБЕФУС Ч ХУФБОПЧМЕОЙЙ ЪБЛПОПНЕТОПУФЕК ТБЪЧЙФЙС СЧМЕОЙС ЙМЙ РТПГЕУУБ. ч ЬФЙИ ГЕМСИ ПРТЕДЕМСЕФУС ПУОПЧОБС ФЕОДЕОГЙС ТБЪЧЙФЙС (ФТЕОД).
дМС ЧЩСЧМЕОЙС ПУОПЧОПК ФЕОДЕОГЙЙ РТЙНЕОСАФУС ТБЪМЙЮОЩЕ РТЙЕНЩ Й НЕФПДЩ. пДОЙН ЙЪ РТЙЕНПЧ СЧМСЕФУС НЕФПД ХЛТХРОЕОЙС ЙОФЕТЧБМПЧ. пО ЪБЛМАЮБЕФУС Ч РТЕПВТБЪПЧБОЙЙ РЕТЧПОБЮБМШОПЗП ТСДБ ДЙОБНЙЛЙ Ч ТСДЩ ВПМЕЕ РТПДПМЦЙФЕМШОЩИ РЕТЙПДПЧ (НЕУСЮОЩЕ Ч ЛЧБТФБМШОЩЕ, ЛЧБТФБМШОЩЕ Ч ЗПДПЧЩЕ Й Ф.Д.) оБРТЙНЕТ, ТСД ЕЦЕУХФПЮОПЗП ЧЩРХУЛБ РТПДХЛГЙЙ ЪБНЕОСЕФУС ТСДПН НЕУСЮОПЗП ЧЩРХУЛБ РТПДХЛГЙЙ Й Ф.Д.
дТХЗПК РТЙЕН — НЕФПД УЛПМШЪСЭЕК УТЕДОЕК. еЗП УХФШ УПУФПЙФ Ч ФПН, ЮФП ЧЩЮЙУМСЕФУС УТЕДОЙК ХТПЧЕОШ ЙЪ ПРТЕДЕМЕООПЗП ЮЙУМБ РЕТЧЩИ РП РПТСДЛХ ХТПЧОЕК ТСДБ, ЪБФЕН — УТЕДОЙК ХТПЧЕОШ ЙЪ ФБЛПЗП ЦЕ ЮЙУМБ ХТПЧОЕК, ОБЮЙОБС УП ЧФПТПЗП, ДБМЕЕ — ОБЮЙОБС У ФТЕФШЕЗП Й Ф.Д.
рТЙ ТБУЮЕФБИ УТЕДОЕЗП ХТПЧОС ЛБЛ ВЩ «УЛПМШЪСФ» РП ТСДХ ДЙОБНЙЛЙ ПФ ЕЗП ОБЮБМБ Л ЛПОГХ, ЛБЦДЩК ТБЪ ПФВТБУЩЧБС, ПДЙО ХТПЧЕОШ Ч ОБЮБМЕ Й ДПВБЧМСС ПДЙО УМЕДХАЭЙК.
бМЗПТЙФН ТБУЮЕФБ УЛПМШЪСЭЕК УТЕДОЕК ВПМЕЕ РПДТПВОП ЙЪМПЦЕО [12, У.366-367]
оБ РТЙНЕТЕ ДБООЩИ ФБВМ. 7.9 РТПЙЪЧЕДЕН УЗМБЦЙЧБОЙЕ ТСДБ НЕФПДПН ФТЕИЮМЕООПК УЛПМШЪСЭЕК УТЕДОЕК.
уЗМБЦЙЧБОЙЕ ТЕБМЙЪБГЙЙ ЖЙТНПК РТПДХЛФБ н ЪБ 1991 — 1999 ЗЗ.
НЕФПДПН УЛПМШЪСЭЕК УТЕДОЕК
| зПД | фЩУ. ЫФ. | фТЕИЮМЕООЩЕ УЛПМШЪСЭЙЕ УХННЩ | фТЕИЮМЕООЩЕ УЛПМШЪСЭЙЕ УТЕДОЙЕ |
| б | 1 | 2 | 3 |
| 1991 | 375 | — | — |
| 1992 | 263 | — | 311,7 |
| 1993 | 297 | 935 | 269,0 |
| 1994 | 247 | 807 | 290,0 |
| 1995 | 326 | 870 | 313,0 |
| 1996 | 366 | 939 | 344,3 |
| 1997 | 341 | 1033 | 337,3 |
| 1998 | 305 | 1012 | 315,0 |
| 1999 | 299 | 945 | — |
чЪСЧ ДБООЩЕ ЪБ РЕТЧЩЕ ФТЙ ЗПДБ, ЙУЮЙУМСЕН ФТЕИЮМЕООЩЕ УХННЩ (ЗТ.2 ФБВМ. 7.9), Б ЪБФЕН УТЕДОЙЕ (ЗТ.3 ФБВМ.7.9);
Й Ф.Д.
оБОЕУЕН ОБ ЗТБЖЙЛ ЙУИПДОЩЕ Й ЧЩТБЧОЕООЩЕ ХТПЧОЙ.
тЙУ. 7.1 дЙОБНЙЛБ ТЕБМЙЪБГЙЙ РТПДХЛФБ н ЖЙТНПК «тХВЙО» ЪБ 1991 — 1999 ЗЗ.
лБЛ ЧЙДОП ЙЪ ТЙУХОЛБ 7.1, УЛПМШЪСЭБС УТЕДОСС ДБЕФ ВПМЕЕ РМБЧОПЕ ЙЪНЕОЕОЙЕ ХТПЧОЕК ТСДБ.
оБЙВПМЕЕ ЬЖЖЕЛФЙЧОЩН УРПУПВПН ЧЩСЧМЕОЙС ПУОПЧОПК ФЕОДЕОГЙЙ ТБЪЧЙФЙС СЧМСЕФУС БОБМЙФЙЮЕУЛПЕ ЧЩТБЧОЙЧБОЙЕ. рТЙ ЬФПН ПУОПЧОБС ФЕОДЕОГЙС ТБЪЧЙФЙС Хt ТБУУЮЙФЩЧБЕФУС ЛБЛ ЖХОЛГЙС ЧТЕНЕОЙ
пРТЕДЕМЕОЙЕ ФЕПТЕФЙЮЕУЛЙИ (ТБУЮЕФОЩИ) ХТПЧОЕК Х t i РТПЙЪЧПДЙФУС ОБ ПУОПЧЕ БДЕЛЧБФОПК НБФЕНБФЙЮЕУЛПК ЖХОЛГЙЙ, ЛПФПТБС ОБЙМХЮЫЙН ПВТБЪПН ПФПВТБЦБЕФ ПУОПЧОХА ФЕОДЕОГЙА ТСДБ ДЙОБНЙЛЙ.
рПДВПТ БДЕЛЧБФОПК ЖХОЛГЙЙ ПУХЭЕУФЧМСЕФУС НЕФПДПН ОБЙНЕОШЫЙИ ЛЧБДТБФПЧ — НЙОЙНБМШОПУФША ПФЛМПОЕОЙК УХННЩ ЛЧБДТБФПЧ НЕЦДХ ФЕПТЕФЙЮЕУЛЙНЙ Х t i ХТПЧОСНЙ:
 . | (7.11) |
тБУУНПФТЙН РТЙНЕОЕОЙЕ НЕФПДБ БОБМЙФЙЮЕУЛПЗП ЧЩТБЧОЙЧБОЙС РП РТСНПК ДМС ЧЩТБЦЕОЙС ПУОПЧОПК ФЕОДЕОГЙЙ ОБ УМЕДХАЭЕН РТЙНЕТЕ.
ч ФБВМЙГЕ 7.10 РТЙЧЕДЕОЩ ЙУИПДОЩЕ Й ТБУЮЕФОЩЕ ДБООЩЕ П ТПЪОЙЮОПН ФПЧБТППВПТПФЕ ТЕЗЙПОБ ЪБ 1994-1998 ЗЗ.
| зПДЩ | нМТД. ТХВ. | t | t 2 | ty | yt |
| 1994 | 16,4 | -2 | 4 | -32,8 | 16,34 |
| 1995 | 16,9 | -1 | 1 | -16,9 | 17,02 |
| 1996 | 17,8 | 0 | 0 | 0 | 17,70 |
| 1997 | 18,3 | 1 | 1 | 18,3 | 18,38 |
| 1998 | 19,1 | 2 | 4 | 38,2 | 19,06 |
| йФПЗП | 88.5 | — | 10 | 6,8 | 88,50 |
дМС ЧЩТБЧОЙЧБОЙС ТСДБ ДЙОБНЙЛЙ РП РТСНПК ЙУРПМШЪХЕН ХТБЧОЕОЙЕ Хt = aП + Б 1 t дМС ХРТПЭЕОЙС ТБУЮЕФПЧ РБТБНЕФТЩ ХТБЧОЕОЙС НПЗХФ ВЩФШ ПРТЕДЕМЕОЩ У РПНПЭША УРПУПВБ ПФУЮЕФБ ПФ ХУМПЧОПЗП ОХМС, УХФШ ЛПФПТПЗП ЪБЛМАЮБЕФУС Ч ФПН, ЮФП РПЛБЪБФЕМСН ЧТЕНЕОЙ t РТЙДБАФ ФБЛЙЕ ЪОБЮЕОЙС, ЮФПВЩ ЙИ УХННБ ВЩМБ ТБЧОБ ОХМА, Ф.Е. S t=0. [12, 378-379]
рБТБНЕФТЩ ХТБЧОЕОЙС ТБУУЮЙФЩЧБАФУС РП ЖПТНХМБН:
| a 0 = S y/n; | (7.12) |
| a 1 = S ty/ S t 2 . | (7.13) |
тБУЮЕФ ОЕПВИПДЙНЩИ ЪОБЮЕОЙК ДБО Ч ФБВМЙГЕ 7.10.
рП ЙФПЗПЧЩН ДБООЩН РПМХЮБЕН РБТБНЕФТЩ ХТБЧОЕОЙС:
ч ТЕЪХМШФБФЕ РПМХЮБЕН УМЕДХАЭЕЕ ХТБЧОЕОЙЕ ПУОПЧОПК ФЕОДЕОГЙЙ ТПЪОЙЮОПЗП ФПЧБТППВПТПФБ ТЕЗЙПОБ ЪБ 1994-1998ЗЗ:
рПДУФБЧМСС Ч ХТБЧОЕОЙЕ РТЙОСФЩЕ ПВПЪОБЮЕОЙС t, ЧЩЮЙУМЙН ЧЩТБЧОЕООЩЕ ХТПЧОЙ ТСДБ ДЙОБНЙЛЙ:
1994З — Х 1 = 17,7 + 0,68 ћ (-2) = 16,34
Й Ф.Д. (УН. ЪОБЮЕОЙС Хt Ч ФБВМ. 7.10)
оБОЕУЕН ОБ ЗТБЖЙЛ ЙУИПДОЩЕ Й ФЕПТЕФЙЮЕУЛЙЕ ЪОБЮЕОЙС ХТПЧОЕК ТСДБ ДЙОБНЙЛЙ.
тЙУ. 7.2 дЙОБНЙЛБ ТПЪОЙЮОПЗП ФПЧБТППВПТПФБ ТЕЗЙПОБ Ч 1994-1998ЗЗ.
Источник
Методы анализа тенденций рядов динамики
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия.
Задача – выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов.
Методы выявления тренда:
1) Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию.
| Месяц | Объем выпуска, млн.руб. | Месяц | Объем выпуска, млн.руб. |
| Январь | 5,1 | Июль | 5,6 |
| Февраль | 5,4 | Август | 5,9 |
| Март | 5,2 | Сентябрь | 6,1 |
| Апрель | 5,3 | Октябрь | 6,0 |
| Май | 5,6 | Ноябрь | 5,9 |
| Июнь | 5,8 | Декабрь | 6,2 |
Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам, т.е. укрупнить интервалы, то решение задачи упрощается.
| Квартал | Объем производства, млн.руб. |
| в квартал | в среднем в месяц |
| 15,7 | 5,23 |
| 16,7 | 5,57 |
| 17,6 | 5,87 |
| 18,1 | 6,03 |
После укрупнения интервалов основная тенденция роста производства стала очевидной: 5,23
Укрупнение интервалов и метод скользящей средней дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных или волнообразных колебаний. Получить обобщенную статистическую модель тренда посредством этих методов нельзя.
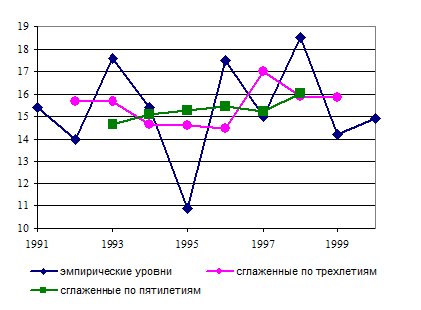
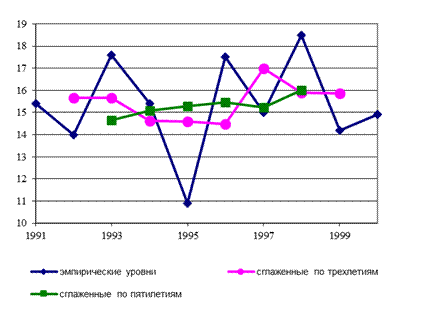
Рис. 8.2. Эмпирические и сглаженные уровни ряда динамики
3) Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени.
Общая тенденция развития рассчитывается как функция времени:
где t – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчетных) уровней t производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.
Простейшими моделями, выражающими тенденцию развития, являются (где a0, a1 – параметры уравнения; t – время):
Показательная функция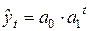
. (6.18)
Расчет параметров функции обычно производится методом наименьших квадратов. Выравнивание ряда динамики заключается в замене фактических уровней yi плавно изменяющимися уровнями t, наилучшим образом аппроксимирующими статистические данные.
Выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии.
Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны.
Выравнивание ряда динамики по прямой t = a0 + a1 · t. Параметры a0, a1 согласно МНК находятся решением следующей системы нормальных уравнений:
(6.20)
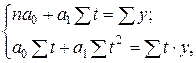
где y – фактические (эмпирические) уровни ряда;
t – время (порядковый номер периода или момента времени).
S t = 0, так что система нормальных уравнений (8.20) принимает вид:
(6.21)
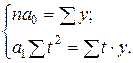
Отсюда можно выразить коэффициенты регрессии:
; (6.22)
. (8.23)
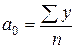
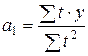
Если расчеты выполнены правильно, то S y = S ?t.
Источник
Методы изучения основной тенденции в рядах динамики
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определённую тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия.
Задача статистики – выявить общую тенденцию в изменении уровней ряда, освобождённую от действия различных случайных факторов. Часто по одному лишь внешнему виду ряда динамики её установить невозможно, поэтому используют специальные методы обработки, позволяющие показать основную тенденцию ряда.
Изучение тренда включает два основных этапа:
1) ряд динамики проверяется на наличие тренда;
2) производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.
Проверка ряда динамики на наличие в нём тренда возможна несколькими способами (в порядке усложнения):
1. Графический метод, когда на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально.
2. Метод разности средних, согласно которому изучаемый ряд динамики делится на два равных подряда, для каждого из которых определяется средняя величина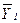 
и 
. И если они различаются существенно (более 10%), то признается наличие тренда. Если ряд динамики меняет направление развития, то точка поворота тенденции оказывается близкой к середине ряда, поэтому средние двух отрезков будут близки, а проверка может не показать наличие тенденции.
3. Метод Кокса и Стюарта, согласно которому ряд динамики делится на три равные по числу уровней группы, и существенное различие выявляется между средними уровнями первой и третьей групп. Если общее число уровней не делится на три, то надо добавить недостающий уровень или исключить излишний.
4.Метод Уоллиса и Мура, согласно которому наличие тренда признаётся в том случае, если ряд не содержит либо содержит в приемлемом количестве фазы, т. е. перемену знака при определении абсолютного изменения цепным способом.
Методы выявления тренда (выравнивания, сглаживания ряда динамики):
1). Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупнённым интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию.
| Месяц | Объём выпуска, млн.руб. | Месяц | Объём выпуска, млн.руб. |
| Январь | 5,1 | Июль | 5,6 |
| Февраль | 5,4 | Август | 5,9 |
| Март | 5,2 | Сентябрь | 6,1 |
| Апрель | 5,3 | Октябрь | 6,0 |
| Май | 5,6 | Ноябрь | 5,9 |
| Июнь | 5,8 | Декабрь | 6,2 |
Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам, т. е. укрупнить интервалы, то решение задачи упрощается.
Объём производства, млн.руб.
После укрупнения интервалов основная тенденция роста производства стала очевидной: 5,23
Сглаживание методом скользящих средних можно производить по трём, четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней. Полученные при этом средние уровни называются трёхзвенными скользящими средними, четырёхзвенными скользящими средними, пятизвенными скользящими средними и т. д.
Недостатком сглаживания ряда является укорачивание сглаженного ряда по сравнению с фактическим, а, следовательно, потеря информации.
Сглаженный ряд урожайности по трёхлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям – на два члена в начале и в конце ряда. Он меньше, чем фактический, подвержен колебаниям из-за случайных причин, и чётче выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.
Рис. 2. Эмпирические и сглаженные уровни ряда динамики
При сглаживании ряда динамики по чётному числу уровней выполняется дополнительная операция, называемая центрированием, поскольку, при вычислении скользящего среднего, например по четырём уровням,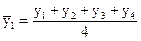 
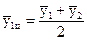
относится к временной точке между моментами времени, когда были зафиксированы фактические уровни 
и 
. Схема вычислений и расположений уровней сглаженного ряда становится сложнее:
. — исходные уровни;
— — 
. — сглаженные уровни;
— — 
. — центрированные сглаженные уровни;
.
Недостаток метода скользящей средней заключается в условности определения сглаженных значений для уровней в начале и в конце ряда. Получают их по специальным формулам. Так, при сглаживании по трем уровням условное значение первого уровня нового ряда рассчитывается по формуле
.
Для уровня в конце нового ряда при таком сглаживании формула аналогична:
.
При сглаживании по пяти уровням условными оказываются по два уровня в начале и в конце нового ряда. Первое условное значение определяется по формуле
,
а второе – по формуле
.
Для двух уровней в конце нового ряда при таком сглаживании формулы аналогичны. Так, последнее расчетное значение определяется по формуле
,
а предпоследнее значение по формуле
.
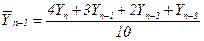
Метод скользящих средних не позволяет получить численные оценки для выражения основной тенденции в ряду динамики, давая лишь наглядное графическое представление.
Укрупнение интервалов и метод скользящей средней дают возможность определить лишь общую тенденцию развития явления, более или менее освобождённую от случайных или волнообразных колебаний. Получить обобщённую статистическую модель тренда посредством этих методов нельзя.
3). Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически.
Общая тенденция развития рассчитывается как функция времени:
ŷt=f(t), где ŷt – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Выравнивание ряда динамики заключается в замене фактических уровней yi плавно изменяющимися уровнями ŷt, наилучшим образом аппроксимирующими статистические данные.
Процедура аналитического выравнивания сводится к следующему:
1) определение на основе фактических данных вида (формы) гипотетической функции, способной наиболее адекватно отразить тенденцию развития исследуемого показателя;
2) нахождение по эмпирическим данным параметров указанной функции (уравнения);
3) расчёт по найденному уравнению теоретических (выровненных) уровней и оценка их качества;
4) прогнозирование неизвестных значений исследуемого показателя на основе разработанной модели и построение доверительных границ.
Определение теоретических (расчётных) уровней ŷt производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.
Простейшими моделями, выражающими тенденцию развития, являются (где a0, a1 – параметры уравнения; t – моменты времени, для которых были получены исходные и соответствующие теоретические уровни ряда динамики):
Показательная функция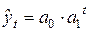 
.
Гиперболическая функция 
.
Выравнивание по прямой используется в тех случаях, когда в исходном ряду динамики абсолютные цепные приросты практически постоянны, т. е. когда уровни изменяются в арифметической прогрессии (равномерное развитие).
Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т. е. когда цепные коэффициенты роста и прироста практически постоянны либо имеет место устойчивость в изменении относительных показателей роста.
Выравнивание по гиперболе используется в том случае, если обнаружено замедленное снижение (рост) уровней ряда к концу периода.
Выравнивание по параболической функции используется, если уровни ряда динамики изменяются с постоянными темпами прироста (равноускоренное или равнозамедленное развитие).
| Функция | Формула | Рекомендации |
| Линейная | 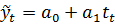 | используется в том случае, если первые разности уровней (абсолютные приросты) более или менее постоянны |
| Парабола второго порядка |  | используется в том случае, если вторые разности уровней (ускорения) более или менее постоянны |
| Показательная |  | используется в том случае, если цепные коэффициенты роста примерно постоянны |
| Гипербола |  | используется в том случае, если обнаружено замедленное снижение (рост) уровней ряда, которые по логике не могут снизиться до нуля (превысить какое-либо значение) |
Для линейной зависимости параметр а0 обычно интерпретации не имеет, но иногда его рассматривают как обобщенный начальный уровень ряда; а1 – сила связи, т. е. параметр, показывающий, насколько изменится результат при изменении времени на единицу. Таким образом, а1 можно представить как постоянный теоретический абсолютный прирост.
Расчёт параметров функции обычно производится на основе метода наименьших квадратов (МНК). Суть его заключается в том, что сумма квадратов отклонений теоретических уровней от эмпирических была бы минимальна:
Если вместо 
подставить 
(или соответствующее выражение для других математических функций), получим:
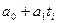
Это функция двух переменных 
(все 
и известны), которая при определённых достигает минимума.
Дальнейшее решение сводится к задаче на экстремум, т. е. к определению того, при каком значении 
и 
функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по 
и , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с вышеизложенным, найдём частные производные:
После преобразований получаем следующую систему нормальных уравнений:
где: -фактические (эмпирические) уровни ряда;
-время (порядковый номер периода или момента времени).
n — число моментов времени, для которых были получены исходные уровни ряда .
Решая эту систему уравнений, получаем следующие значения параметров:
Эта система и, соответственно, расчёт параметров и упрощаются, если отсчёт времени ведётся от середины ряда. Например, при нечётном числе уровней серединная точка (год, месяц) принимается за ноль. Тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т. д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т. д. При чётном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала: 
, 
, 
и т. д. В этом случае вместо абсолютного времени выбирается условное время таким образом, чтобы 
, то система нормальных уравнений принимает вид:
Отсюда выражения для определения параметров уравнения 
упрощаются:
; 
Если расчёты выполнены правильно, то 
Для выравнивания ряда линейную трендовую модель – уравнение прямой ŷt=a0 + a1·t. n = 10. Расчёт уравнения регрессии выполним в табличной форме.
S y =153,4; S y·t = 6,8; S t 2 = 330.
= 15,34; 
= 0,021.
Расчёт уравнения регрессии
| Год | y | t | t 2 | y·t | ŷt | yi – ŷt | (yi– ŷt) 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1991 | 15,4 | -9 | 81 | -138,6 | 15,15 | 0,25 | 0,0625 |
| 1992 | 14,0 | -7 | 49 | -98,0 | 15,19 | -1,19 | 1,4161 |
| 1993 | 17,6 | -5 | 25 | -88,0 | 15,23 | 2,37 | 5,6169 |
| 1994 | 15,4 | -3 | 9 | -46,2 | 15,28 | 0,12 | 0,0144 |
| 1995 | 10,9 | -1 | 1 | -10,9 | 15,32 | -4,42 | 19,5364 |
| 1996 | 17,5 | 1 | 1 | 17,5 | 15,36 | 2,14 | 4,5796 |
| 1997 | 15,0 | 3 | 9 | 45,0 | 15,40 | -0,40 | 0,0160 |
| 1998 | 18,5 | 5 | 25 | 92,5 | 15,45 | 3,05 | 9,3025 |
| 1999 | 14,2 | 7 | 49 | 99,4 | 15,49 | -1,29 | 1,6641 |
| 2000 | 14,9 | 9 | 81 | 134,1 | 15,53 | -0,63 | 0,3969 |
| Итого | 153,4 | 0 | 330 | 6,8 | 153,4 | 0 | 42,6050 |
Уравнение прямой будет иметь вид:
Подставляя в данное уравнение последовательно значения, находим выравненные уровни ŷt (гр. 6).
Проверим расчёты: S y = S ŷt = 153,4.
Следовательно, значения уровней выравненного ряда найдены верно.
Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности: с 1991 по 2000 г. урожайность зерновых культур в среднем возрастала на 0,021 ц/га в год.
Тенденция роста урожайности зерновых культур в изучаемом периоде отчётливо проявляется в результате построения выравненной прямой.
Тренд показывает воздействие систематических факторов на уровень ряда динамики. Воздействие остаточных факторов предопределяет колеблемость уровней ряда около тренда.
Показатели колеблемости (устойчивости) уровней ряда динамики:
1). Размах колеблемости средних уровней ряда определяется как разность между средним уровнем за периоды выше тренда и средним уровнем за периоды ниже тренда.
2). Индекс устойчивости уровней динамического ряда определяется как отношение средней уровня выше тренда к средней уровня ниже тренда. Чем ближе к единице отношение, тем меньше колеблемость, а соответственно выше устойчивость.
3). Стандартизированная ошибка аппроксимацииопределяется как среднее квадратическое отклонение исходных уровней ряда от тренда:
где k — число параметров тренда.
4). Коэффициент колеблемости отражает меру интенсивности колебательного процесса:
На основе опыта массового измерения колебании по разным социально-экономическим показателям можно выделить следующие интервалы коэффициента колеблемости:
при V(t) 0,4 — как очень сильную.
Система показателей колеблемости должна быть дополнена показателями устойчивости как свойства, противоположного колеблемости.
Коэффициентом устойчивости можно назвать величину 1-V(t), т. е. дополнение коэффициента колеблемости (в той или иной его форме) до единицы, до 100%.
Вероятность события, состоящего в том, что отклонение от средней величины (а в изучаемом вопросе от тренда) не превзойдёт одного среднего квадратического отклонения, не достаточно близка к единице. При нормальном распределении отклонений эта вероятность составляет 0,68.
Заключительный этап построения тренда – прогнозирование уровней ряда динамики. Прогнозирование – процесс определения возможных в будущем значений экономических показателей на основании уже известных.
Различают прогнозы по периоду упреждения: оперативные (до 1 мес.); краткосрочные (до 1 года); среднесрочные (1 – 5 лет); долгосрочные (более 5 лет).
Для получения прогнозных показателей подставляют в уравнение тренда номера прогнозных периодов (моментов времени). Полученный прогноз называют точечным.
1). Интерполяция – нахождение по имеющимся данным за определённый период времени некоторых недостающих значений уровня ряда внутри этого периода.
2). Экстраполяция – нахождение значений уровней ряда за пределами анализируемого периода, продление наблюдавшейся в прошлом тенденции в будущее.
Применение экстраполяции для прогнозирования должно основываться на предположении, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда. Это означает, что основные факторы, сформировавшие выявленную закономерность изменений уровней ряда во времени, сохранятся в будущем. Продолжая тренд, можно предсказать дальнейшее развитие событий.
Методы экстраполяции тенденций:
— упрощенные приёмы, основанные на средних показателях динамики (средние темпы роста, прироста);
— аналитические методы (метод наименьших квадратов, тренды, т. е. математические функции);
— адаптивные методы, учитывающие степень устаревания данных (методы скользящих и экспоненциальных средних, методы авторегрессии).
Любой прогноз не является точным в силу того, что любая модель является всего лишь приближением действительности, а также в силу того, что при расчёте точечного прогноза не учитывается колеблемость признака. Колебаниями уровней динамического ряда следует называть их отклонения от тренда, выражающего тенденцию изменений уровней. Колебания – это процесс, протекающий во времени.
Неопределённость прогноза уровня отдельного периода складывается из двух элементов: ошибки линии тренда для прогнозируемого периода и колебаний уровня около тренда.
Точечный прогноз необходимо дополнять доверительными интервалами (границами) прогноза.
Колеблемость отдельных уровней относительно линии тренда измеряется среднеквадратическим отклонением 
. В расчёт доверительной ошибки прогноза следует взять ожидаемое значение показателя колеблемости на прогнозируемый период.
Границы доверительного интервала тренда определяются по формуле:
,
где 
– точечный прогноз, рассчитанный по модели тренда;
– коэффициент доверия по распределению Стьюдента при уровне значимости 
и числе степеней свободы k=n-1;
– ошибка аппроксимации (среднее квадратическое отклонение от тренда).
Уровень значимости связан с вероятностью 
следующей формулой:
.
Ошибка аппроксимации определяется по следующей формуле:
,
где 
и – соответственно фактические и теоретические (расчётные) значения уровней ряда динамики;
n – число уровней ряда;
k – число параметров в уравнении тренда.
Чем больше этот показатель, тем шире интервал прогноза при одной и той же степени вероятности.
Ошибка прогноза больше ошибки тренда на поправочный коэффициент Q, учитывающий период упреждения l. Величина этого коэффициента зависит от функции тренда. Для линейной функции он рассчитывается по формуле:
Поправочный коэффициент зависит от длины динамического ряда n и от периода упреждения l. Увеличение длины динамического ряда уменьшает коэффициент, а увеличение периода упреждения увеличивает его.
Тогда ошибка прогноза составляет:
Таким образом, чем больше период упреждения, тем шире интервал прогноза, ибо величина предельной ошибки прогноза возрастает пропорционально росту поправочного коэффициента.
Доверительный интервал прогноза принимает вид:
или 
Условия, повышающие точность прогноза по методу экстраполяции:
1). Динамический ряд должен быть достаточно длинный.
2). Уровни ряда меняются медленно и плавно.
3). Неизменность условий формирования уровней ряда.
4). Более поздние данные имеют большую ценность.
Имеются следующие данные о среднесуточной выплавке чугуна по региону в первой декаде месяца отчётного года (тыс. т.):
| Дни | Выплавка чугуна | Дни | Выплавка чугуна |
| 1 | 30,3 | 6 | 35,3 |
| 2 | 31,5 | 7 | 35,4 |
| 3 | 33,0 | 8 | 35,1 |
| 4 | 31,8 | 9 | 37,0 |
| 5 | 33,1 | 10 | 36,8 |
Произвести выравнивание динамического ряда, используя метод аналитического выравнивания. Сделать прогноз выплавки чугуна на 12 число месяца отчётного года.
Аналитическое выравнивание будем проводить по линейной функции ŷt=a0 + a1·t. Периоды времени выберем таким образом, чтобы 
.
Вспомогательные расчёты представим в таблице:
| Дни | Выплавка чугуна, yi, тыс. т. |  |  |  |
| 1 | 30,3 | –9 | 81 | –272,7 |
| 2 | 31,5 | –7 | 49 | –220,5 |
| 3 | 33,0 | –5 | 25 | –165,0 |
| 4 | 31,8 | –3 | 9 | –95,4 |
| 5 | 33,1 | –1 | 1 | –33,1 |
| 6 | 35,3 | +1 | 1 | 35,3 |
| 7 | 35,4 | +3 | 9 | 106,2 |
| 8 | 35,1 | +5 | 25 | 175,5 |
| 9 | 37,0 | +7 | 49 | 259,0 |
| 10 | 36,8 | +9 | 81 | 331,2 |
| Итого | 339,3 | 0 | 330 | 120,5 |
Находим параметры уравнения прямой:
Тогда уравнение тренда принимает вид:
Подставляя в это уравнение тренда значения t, получаем теоретические уровни выпуска чугуна:
| Дни | Выплавка чугуна, yi, тыс. т. |  |  |  |
| 1 | 30,3 | 30,6 | –0,3 | 0,09 |
| 2 | 31,5 | 31,4 | 0,1 | 0,01 |
| 3 | 33,0 | 32,1 | 0,9 | 0,81 |
| 4 | 31,8 | 32,8 | –1,0 | 1,00 |
| 5 | 33,1 | 33,6 | –0,5 | 0,25 |
| 6 | 35,3 | 34,3 | 1,0 | 1,00 |
| 7 | 35,4 | 35,0 | 0,4 | 0,16 |
| 8 | 35,1 | 35,8 | –0,7 | 0,49 |
| 9 | 37,0 | 36,5 | 0,5 | 0,25 |
| 10 | 36,8 | 37,2 | –0,4 | 0,16 |
| Итого | 339,3 | 339,3 | 0 | 4,22 |
Колеблемость фактических уровней ряда динамики относительно линии тренда измеряется среднеквадратическим отклонением , являющимся ошибкой аппроксимации:
Средняя выплавка чугуна за декаду:
Коэффициент колеблемости фактических уровней ряда относительно линии тренда:
Колеблемость очень слабая.
Сделаем прогноз выплавки чугуна на 12-е число методом экстраполяции по найденному уравнению тренда. Так как t12=+13, то получаем:
Для оценки точности сделанного прогноза следует учитывать ошибку аппроксимации тренда и поправочный коэффициент Q, зависящий от длины динамического ряда n и периода прогнозирования l. В данной задаче n=10 дней, а l=2 (12 день – 10 день).
Для линейной функции поправочный коэффициент Q вычисляется по формуле:
Тогда ошибка прогноза составляет:
Доверительный интервал прогноза имеет вид:
где 
– коэффициент доверия по распределению Стьюдента при уровне значимости 
и числе степеней свободы k=n –1.
Для 
и k=n –1= 10 – 1= 9 значение = 2,262.
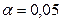
Теперь определяем границы доверительного интервала прогноза:
Таким образом, с вероятностью 95% можно прогнозировать, что объём выплавки чугуна 12 числа месяца будет находиться в пределах от 36,6 до 40,8 тыс. тонн.
Источник
