Способом выделения полных квадратов

Выделение полного квадрата — формулы, методы и примеры решений

Однако не все его знают. В результате этого объем вычислений увеличивается, а также допускаются ошибки. Он также применяется для нахождения корней уравнений и построения графиков.

Общая информация

Выделить полный квадрат из многочлена второй степени означает, что его следует привести к более читабельной формуле. Эта операция применяется в следующих случаях: интегрирование, дифференцирование, построение графиков и решение уравнений (чаще — в последних двух).

За основу взяты три формулы сокращенного умножения (разложение квадратного многочлена на множители), которые специалисты рекомендуют запомнить или выписать отдельно.

К ним относятся следующие соотношения:

1. Квадрат суммы: (y + z)^2 = y 2 + 2yz + z 2 .
2. Квадрат разности: (y — z)^2 = y 2 — 2yz + z 2 .
3. Разность квадратов: y 2 — z 2 = (y — z)(y + z).

Существует правило, позволяющее выполнить операцию упрощения многочлена ay 2 + by + c второй степени путем разложения его на множители. Это означает, что его следует свести (преобразовать) к виду a * (y — y0)^2 + y0.

Универсальный алгоритм

Алгоритмом называется комплексное решение, состоящее из последовательного набора правил. Преобразование ay 2 + by + c осуществляется следующим образом:

1. Привести к такому виду первое слагаемое на основании формулы (y + z)^2 = y 2 + 2yz + z 2 : [(a)^(½) * y]^2. Корень из коэффициента «а» следует указывать обязательно.
2. Второе слагаемое должно состоять из удвоенного произведения: by = [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)].
3. Третий свободный член находится по формуле z = (b / [2 * (a)^(½)].
4. Для равновесия следует отнять число, полученное в пункте 3.
5. Записать результат нужно таким образом: [(a)^(½) * y]^2 + [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)] + [(b / (2 * (a)^(½))]^2 — [(b / (2 * (a)^(½))]^2 + c.

Для квадрата разности алгоритм похожий. Формула выделения полного квадрата имеет такой вид: [(a)^(½) * y]^2 — [(2 * (a)^(½) * y)] * (b / [2 * (a)^(½)] + [(b / (2 * (a)^(½))]^2 — [(b / (2 * (a)^(½))]^2 + c. Соотношение также применяется математиками в алгебре, а также в различных дисциплинах с физико-математическим уклоном. Для этого нужно воспользоваться таким подробным объяснением правил решения:

1. Запись формулы: ay 2 — c = ((a)^(½) * y — (c)^(½))((a)^(½) * y + (c)^(½)).
2. Коэффициент «с^(½)» должен быть равен целому числу.
3. Если условие во втором пункте не выполняется, то следует воспользоваться таким соотношением: с + a — a= с1 — a.
4. Записать выражение в таком виде: ay 2 — c + a — a = ((a)^(½) * y — (c1)^(½))((a)^(½) * y + (c1)^(½)) — a.

Число «а» может быть положительным или отрицательным. Если его прибавить к «с», то должно получиться значение «с1».

При извлечении квадратного корня результат должен быть целым. Чтобы равенство не нарушалось, следует прибавить и отнять «а».

Алгоритм записан в общем виде. В теории он является сложным для понимания.

Однако при практическом применении некоторые неясности исчезают. Для начала нужно разобрать, где его нужно применять.

Сферы использования

Математики рекомендуют разобрать основные примеры выделения полного квадрата. Следует их систематизировать, поскольку это позволит оптимизировать процесс решения. Основной смысл заключается в применении соответствующих алгоритмов для экономии времени.

Некоторые считают, что шаблонами пользоваться нежелательно. Однако в этом есть и свои положительные стороны. Например, при поступлении в какое-либо высшее учебное заведение следует придерживаться общепринятых вариантов решения. При успешном зачислении в университет можно применить нестандартные подходы выполнения задания.

Шаблоны широко применяются не только в дисциплинах с физико-математическим уклоном, но и в программировании.

Распространенными заданиями с упрощением квадратного трехчлена являются:

• построение графиков квадратичной функции;
• решение уравнений;
• упрощение выражений.

Для нахождения решений следует подробно разобрать алгоритмы. Нет необходимости заучивать основные определения, формулы и правила. Их следует понимать, поскольку в философии есть такой закон: «переход количества в качество». Кроме того, программистами были созданы специальные онлайн-калькуляторы, позволяющие получить полный квадрат, разложить многочлен на множители и так далее.

Построение графиков

Графиком квадратичной функции z = a[y — c]^2 + d является кривая, которая называется параболой. Далее следует ввести следующие пояснения:

1. Коэффициенты «а» и «с» — некоторые числа. Последнее вычисляется по такой формуле: с = b / 2a.
2. Константа «d» является свободным членом.

Следует отметить, что расположение графика функции зависит от вышеописанных коэффициентов. Для построения параболы математики рекомендуют разобрать частные случаи:

Направление ветвей: вверх (a > 0) и вниз (a 0), по ОУ в отрицательном направлении (c 2 + bz + с = 0 означает найти все его корни или доказать, что их нет. Его можно решать несколькими методами: нахождение дискриминанта, использование теоремы Виета или представление в виде квадрата.

При использовании первого метода нужно воспользоваться таким алгоритмом:

1. Упростить выражение (выведение общего множителя, раскрытие скобок и приведение подобных слагаемых).
2. Вычисление дискриминанта: D = (-b)^2 — 4ac.
3. Разобрать частные случаи, и выбрать ход решения, который зависит от значения D: при D > 0 решением уравнения являются два значения или корня (z1 = -b — D^(½) / 2a и z2 = -b + D^(½) / 2a; D = 0 — один корень (z = -b / 2a) и D 2 + c = 0), то дискриминант можно не высчитывать. Решение находится следующим образом:

1. Нужно перенести свободный член «с» в правую сторону. Если с 0, необходимо перейти ко второму шагу решения.
2. Разделить обе части на «а».
3. Вычислить корни по формулам (будут одинаковыми числами, но с разными знаками): z1 = -[c/a]^(½) z2 = [c/a]^(½).

Когда коэффициент с = 0 (az 2 + bz = 0), то решить уравнение очень просто.

Для этого нужно произвести такие действия:

1. Сократить обе части на «a».
2. Вынести за скобку общий множитель: z (z + b/a) = 0.
3. Решить два уравнения: z1 = 0 и z2 + b/a = 0.
4. Проверить корни, подставив в исходное тождество.

Третий способ — выделение квадрата или использование формул сокращенного умножения. В этом случае нет необходимости использовать стандартный первый метод. Если построить график функции, то корнями будут являться его точки пересечения с осью абсцисс. Можно получить решения при помощи математических преобразований. Последний считается менее точным способом, поскольку корнями могут быть иррациональные числа, а не действительные.

Упрощение выражений

Бывают случаи, когда следует решить уравнение, упростив его. Например, чтобы решить равенство (2z 2 — 5z + 7) + (z + 5)(z + 3) = 0, нужно раскрыть скобки, а затем привести подобные слагаемые. Этот способ называется методом математических преобразований.

В некоторых случаях следует возвести в квадрат, а затем привести подобные слагаемые. После этого необходимо опять воспользоваться формулами, сгруппировав элементы.

Этот шаг позволяет оптимизировать процесс вычислений. Например, нет необходимости подставлять численные значения в выражение z 2 + 4z + 16 + z 2 — 16. Его можно просто упростить: z 2 + 8z + 16 + z 2 — 16 = (z + 4)^2 + (z — 4)(z + 4) = (z + 4)(z + 4 + z — 4) = 2z (z + 4).

Пример решения

Необходимо решить квадратное уравнение z^2 + 20z + 50 = 6z + 5 несколькими способами, используя следующие методы: нахождение дискриминанта, формул разложения, теоремы Виета и построить график. Вычисление корней первым методом (через дискриминант) выглядит таким образом:

1. Упростить выражение: z^2 + 20z + 50 — 6z — 5 = z^2 + 14z + 45.
2. Вычислить дискриминант: D = 14^2 — 4 * 1 * 45 = 196 — 180 = 16 = 4^2.
3. Осуществить анализ второго пункта: если D = 16 > 0, то значит у уравнения два корня.
4. Первый корень: z1 = (-14 — 4) / 2 = -9.
5. Второе решение: z2 = (-14 + 4) / 2 = -5.
6. Проверка: (-9)^2 + (-9) * 14 + 45 = 81 — 126 + 45 = 0 и (-5)^2 + (-5) * 14 + 45 = 25 — 70 + 45 = 0.

Два корня подходят, поскольку равенство 0 = 0 соблюдается. Специалисты рекомендуют опускать проверку, поскольку задача решается несколькими способами.

Второй метод заключается в использовании теоремы Виета. Произвести поиск корней довольно просто, поскольку а = 1. Воспользовавшись формулами z1 + z2 = — 14 и z1 * z2 = 45, можно подобрать корни: z1 = -9 и z2 = -5.

Третий метод заключается в использовании формул разложения. Их разрешается применять несколько раз и в любом порядке. Алгоритм решения выглядит таким образом:

1. Разложить на множители (формула квадрат суммы): z^2 + 14z + 45 = z^2 + 14z + 45 + 4 — 4 = (z^2 + 14z + 49) — 4 = (z + 7)^2 — 4.
2. Использовать формулу разности квадратов двух чисел: (z + 7)^2 — 4 = (z + 7 — 2)(z + 7 — 2) = (z + 5)(z + 9).
3. Записать в виде уравнений: (z + 5) = 0 и (z + 9) = 0.
4. Корни: z1 = -5 и z2 = -9.

Использование графического метода позволит получить точные значения, поскольку во всех предыдущих способах они являются целыми числами. Необходимо записать уравнения параболы (можно воспользоваться вторым пунктом алгоритма третьего метода): (z + 7)^2 — 4. Анализ перед построением выглядит таким образом:

Источник

∑ Некоторые алгебраические понятия — определения и работа с ними

Метод выделения полного квадрата

Итак, традиционно корни многочлена находят, разложив его на множители. Разложение на множители очень помогает в поиске корней, так как, если произведение равно нулю, то один из множителей равен 0. При разложении на множители помогает вынесение общего множителя за скобку (пожалуй, это первое, что следует делать при разложении на множители). Далее обычно происходит группировка (если нет общего множителя, или этого не достаточно). Это по аналогии можно назвать методом группировки: одночлены разделяются по группам, имеющим общий множитель. Далее в идеале появляется общий множитель у всего выражения, который можно вынести и продолжить разложение. Потом, используя формулы сокращённого умножения, можно закончить разложение.

Однако, есть ещё один приём, заслуживающий отдельного внимания, основанный на формулах квадрата суммы и разности. Метод выделения полного квадрата. Особенность этих формул в том, что в них есть квадраты двух выражений и их удвоенное произведение. Если найти что-то, отдалённо напоминающее квадрат суммы или разности, но без какой-то необходимой части, то её можно прибавить, а затем отнять, тем самым не меняя конечного значения выражения. Далее, свернув квадрат суммы/разности, обычно нужно применить ещё какую-то формулу (например, разности квадратов) или совершить какую-то последовательность действий, и многочлен разложится на множители.

Пример разложения на множители методом выделения полного квадрата: y 4 + 4 ⁢ x 4 = y 2 2 + 2 2 ⁢ x 2 2 + 2 × 2 ⁢ x 2 ⁢ y 2 — 2 × 2 ⁢ x 2 ⁢ y 2 = y 2 + 2 ⁢ x 2 2 — 4 ⁢ x 2 ⁢ y 2 = y 2 + 2 ⁢ x 2 — 2 ⁢ x ⁢ y ⁢ y 2 + 2 ⁢ x 2 + 2 ⁢ x ⁢ y
Метод выделения полного квадрата имеет много применений, связанных с квадратными уравнениями. Его можно применить к квадратному трёхчлену (общему виду квадратного уравнения). a ⁢ x 2 + b ⁢ x + c = a ⁢ x 2 + b a × x + c a = a ⁢ x 2 + b ⁢ 2 a ⁢ 2 ⁢ x + c a = a ⁢ x 2 + 2 ⁢ b 2 ⁢ a + c a ; метод выделения полного квадрата : a ⁢ x 2 + b ⁢ x + c = a ⁢ x 2 + 2 ⁢ b 2 ⁢ a + b 2 4 ⁢ a 2 — b 2 4 ⁢ a 2 + c a = a ⁢ x + b 2 ⁢ a 2 — b 2 4 ⁢ a 2 + c a = a ⁢ x + b 2 ⁢ a 2 — b 2 — 4 ⁢ a ⁢ c 4 ⁢ a
Великолепная иллюстрация к методу выделения полного квадрата из Wikimedia Commons О свойствах и некоторых полезных следствиях получившегося представления можно прочитать здесь. Это ещё одна удобная форма представления квадратичной функции.

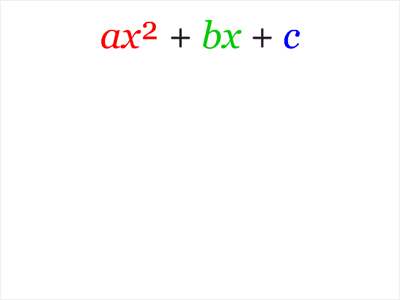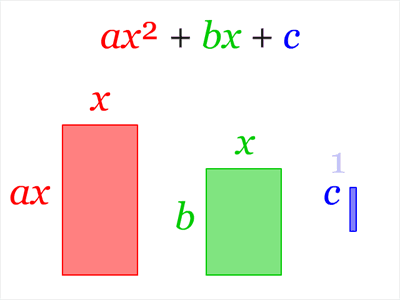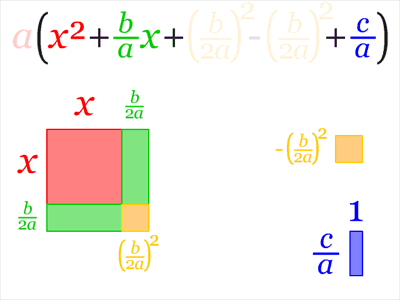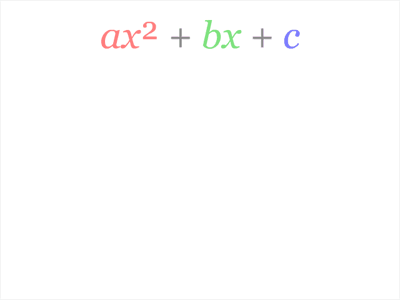
Также метод выделения полного квадрата позволяет именно решать квадратные уравнения. Для этого есть хорошо определённый и вполне известный алгоритм (написан для a x ²+b x +c = 0).

1. Разделить каждую часть на a — старший коэффициент (при квадрате).
2. Вычесть из обеих частей свободный член c/a.
3. Добавить с обеих сторон квадрат половины среднего коэффициента b/a (при x).
4. Свернуть левую часть и упростить правую (если нужно).
5. Произвести два линейных уравнения, приравнивая квадратный корень левой части к положительному и отрицательному квадратному корню правой.
6. Решить получившуюся систему.

У многих квадратных уравнений есть более красивые и простые решения.

Пример нестандартного, но более интуитивного и быстрого решения:
x 2 + 14 ⁢ x + 45 = 0 x 2 + 14 ⁢ x + 45 + 4 — 4 = 0 x 2 + 14 ⁢ x + 49 — 4 = 0 x + 7 2 — 4 = 0 x + 7 2 — 2 2 = 0 x + 7 — 2 ⁢ x + 7 + 2 = 0 x + 5 ⁢ x + 9 = 0 x + 5 = 0 x + 9 = 0 x = — 5 x = — 9 Ответ: x ∈ -5 -9 .
Пример решения уравнения с использованием алгоритма: 4 ⁢ x 2 + 20 ⁢ x — 24 = 0 | × 1 4 x 2 + 5 ⁢ x — 6 = 0 | — — 6 x 2 + 5 ⁢ x = 6 | + 2.5 2 x 2 + 5 ⁢ x + 6.25 = 12.25 x + 2.5 2 = 12.25 x + 2.5 = 3.5 x + 2.5 = — 3.5 x = 1 x = — 6 Ответ: x ∈ 1 — 6 .

Формула корней полного квадратного уравнения

Решение квадратных уравнений с разложением на множители — это достаточно хороший способ решения. Однако, он далеко не единственный. Корни квадратного уравнения также можно вычислять по формуле (используя их зависимость от дискриминанта и коэффициентов — подробнее о дискриминанте и зависимости), но данная формула также выводится, используя описанный выше метод выделения полного квадрата (хотя, как и везде, точное следование заданному алгоритму необязательно, и есть другие (возможно более удобные) пути выведения формулы).

Начнём, как водится, с записи квадратного уравнения общего вида: a x ²+b x +c = 0. А затем, можно проделать над уравнением ряд действий, основанных на алгоритме.

a ⁢ x 2 + b ⁢ x + c = 0 | × 1 a x 2 + b a ⁢ x + с a = 0 x + b 2 ⁢ a 2 = b 2 4 ⁢ a 2 — c a x + b 2 ⁢ a 2 = b 2 — 4 ⁢ a ⁢ c 4 ⁢ a 2
Выражение b² — 4ac называется дискриминантом квадратного уравнения (подробнее о дискриминанте можно прочитать по ссылке выше). Его можно обозначать D.
Получается. x + b 2 ⁢ a = D ⁡ 4 ⁢ a 2 x + b 2 ⁢ a = — D ⁡ 4 ⁢ a 2 Используя свойство квадратного корня из дроби, получаем конечную формулу корней квадратного уравнения. x 1 = — b + D ⁡ 2 ⁢ a x 2 = — b — D ⁡ 2 ⁢ a Это называется основной формулой корней квадратного уравнения. Далее следовало бы обсудить как по дискриминанту определить вид корней и т.д., но это тоже описано по ссылке выше.

Соответственно при решении квадратных уравнений по формуле целесообразно поступать по данному алгоритму.

1. Вычислить дискриминант.
2. Сравнить дискриминант с нулём.
3. Найти корни по формуле.
4. Если дискриминант меньше 0, то уравнение не имеет корней в поле действительных чисел ℝ .

fedor1113
К остальным темам

Источник