Способы геодезических разбивочных работ

Drillings.ru

Торговый дом АУМАС

Тел: +7 (8552) 77-36-15
Моб. тел.: +79053740010, +79600530909, +79656296455
E-mail: drillings@aumas.ru, sale@aumas.ru

Буровые установки (агрегаты, станки) шпиндельного типа

Глубина бурения, м

100 м

300 м

500 м

800 м

2000 м

Буровые установки с подвижным вращателем

Глубина бурения, м

до 15 м.

до 25-50 м.

до 100 м.

до 300 м.

до500 м.

до1000 м.

до2000 м.

Буровые установки роторного типа для бурения скважин

Глубина бурения, м

до 25-50 м.

до 200 м.

600-800 м.

Глубина бурения 2000-3000 м.

Самоходные буровые установки для бурения скважин

Буровые установки и оборудование для глубокого бурения

Источник

Способ прямоугольных координат. Способ полярных координат

Способ прямоугольных координат

Применяется на строительных площадках, где имеется строительная сетка и ведется прямоугольная квартальная застройка(рис 1.). положение точек А и В определяется на местности построением приращений координат и прямых углов.

Рис.1. Способ прямоугольных координат

Аналогично производится вынос осевых знаков от красных линий застройки. Точность перенесения в натуру проектных точек способом прямоугольных координат зависит от точности измерения (отложения) приращений координат, построения прямых углов, ошибок исходных координат, ошибок фиксации (закрепления) точек и рассчитывается по формуле:

где mx и my -ошибки координат пунктов строительной сетки mq0 -погрешность построения угла 900, mф –погрешность фиксации точки А.

Способ полярных координат

Применяется на открытой местности, удобной для измерений расстояний, где отсутствует строительная сетка, путем построения на местности проектных углов ? и полярных расстояний d (рис 2.). Для контроля измеряют величину АВ, если она отличается от проектной более допуска, производится редуцирование точек А и В (смещение в разные стороны на половину величины отклонения).

Рис. 2. Способ полярных координат.

Точность перенесения полярным способом зависит от погрешностей построения угла, линии, исходных данных, закрепления точек (фиксации) и определяется формулой:

где m? погрешность построения угла, md -линии.

Геодезические разбивочные работы – статья на сайте “студент-строитель.ру

Посмотрите также:

Тахеометрическая съемка В основе лежит метод пространственного определения точек местности одним наведением зрительной трубы на рейку, установленную на точке (рис.

Теодолитная съемка Это горизонтальная съемка контуров и предметов местности, выполняемая при создании планов застроенных территорий или подземных коммуникаций в масштабах.

Нивелирование IV класса Общая схема Последовательность работ при нивелировании: 1. Проектирование на карте нивелирных ходов. 2. Рекогносцировка на местности (выбирают.

Источник

СПОСОБ ПРЯМОУГОЛЬНЫХ КООРДИНАТ

Способ прямоугольных координат применяют в основном при наличии на площадке или в цехе промышленного предприятия строительной сетки, в системе координат которой задано положение всех главных точек и осей проекта.

Рис. 19. Схема разбивки способом прямоугольных координат

Разбивку проектной точки С (рис. 19) производят по вычисленным значениям приращений ее координат Δx и Δy от ближайшего пункта сетки. Большее приращение (на рисунке — Δ_y) откладывают по створу пунктов сетки АВ. В полученной точке D устанавливают теодолит и строят от стороны сетки прямой угол. По перпен­дикуляру откладывают меньшее приращение и закрепляют полученную точку С. Для контроля положение точки С можно опреде­лить от другого пункта строительной сетки.

Схема способа прямоугольных координат по существу сочетает в себе схему створно-линейного и полярного способов.

Средняя квадратическая ошибка в положении точки С, опреде­ленной способом прямоугольных координат, может быть выражена формулой

, (68)

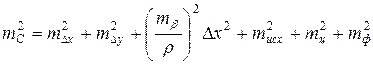
где m_Δxи m_Δy — ошибки отложения приращения координат.

Если по перпендикуляру откладывается ордината, то в формуле (68) величина Δx заменяется на Δy.

Из формулы (58) следует, что большее приращение необ­ходимо откладывать по створу стороны сетки, а меньшее — по перпендикуляру. В этом случае влияние ошибки построения прямо­го угла будет меньшим.

Влияние ошибок в положении исходных пунктов при условии т_A = т_B = т_АB выражается формулой

, (69)

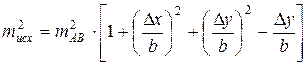
а ошибок центрирования

, (70)

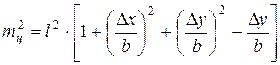
где b — длина стороны строитель­ной сетки.

При разбивке точки С по пер­пендикуляру от стороны абсцисс в формулах (69) и (70) в последнем члене вместо Δy следует принимать Δx.

Рассчитаем для примера точность выноса в натуру проектной точки С, расположенной в середине квадрата строительной сетки со стороной 200 м. Примем относительную ошибку отложения рассто­яния равной 1:10000, т_β = 10″, т_AB = 10 мм, l = 1 мм, m_ф= 1 мм.

Поскольку точка С расположена в середине квадрата строитель­ной сетки, то Δx = Δy =100 м. Для этого случая

мм; m_исх = m_AB = 10 мм;

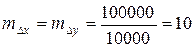
m_ц = l =1 мм; 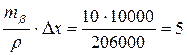мм.

Подставив эти данные в формулу (68) получим

мм.

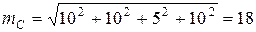
Ошибки центрирования и фиксации можно не учитывать, так как они малы по сравнению с величинами других ошибок.

Источник

Как определить прямоугольные координаты на топографической карте

Координаты являются методом обозначения точки на карте. В картографии используются различные координаты: плоские, прямоугольные, угловые, биполярные и полярные. В целях обозначения объектов недвижимого имущества на топографических картах применяются прямоугольные координаты. Ведь определение прямоугольных координат на топографических картах гораздо проще и точнее.

Понятие прямоугольных координат

Прямоугольные координаты представлены в виде точек пересечения предполагаемых линий по данным взаимно перпендикулярных осей на плоской поверхности. Обычно данные оси на плоскости условно обозначаются латинскими буквами x (абсцисса), y (ордината). Предполагаемые линии, пересечение которых является точкой местоположения, определяются по целым и дробным числовым показателям на указанных осях.

В классической науке такая система носит название декартовая система. Однако классическая система Декарта и применяемая в целях топографического обозначения объектов на карте несколько различаются между собой. Так, в системе расположение осей повернуто на 90 градусов по углу. Названа такая система в честь основателя – Гаусса.

Система Гаусса используется для разделения всей территории Земли на отдельные зоны. Внутри каждой из зон координат идёт обозначение своих числовых выражений предполагаемых линий определения точек. Важным моментом является установление точки отсчёта внутри зоны.

Обычно в качестве такой точки выступает место пересечения срединного меридиана в полосе с экватором планеты. Данная точка не имеет материальной величины, так что обозначается она в качестве нулевой отметки, а её значение всегда равно нулю.

В целом такая система имеет вид сетки с бесконечным количеством числовых значений. Там могут отображаться две группы числовых значений:

1. Значения со знаком минус – для обозначения объектов, находящихся южнее и к западу нулевой отметки.
2. Положительные числовые значения – для указания мест расположения точек восточнее и севернее центральной точки системы координат.

Однако это не полная характеристика значений, указываемых в прямоугольных координатах точек на топографических картах. К примеру, при обозначении точек расположения на топографических картах отрицательные значение не используются.

Обозначения точек на топографических картах при помощи прямоугольных координат

Координатные зоны по системе Гаусса по всей земной поверхности пронумерованы. При обозначении точек на отдельных зонах помимо координат внутри самой зоны указывается номер, который приурочен к указанному квадрату по системе Гаусса.

Данный номер указывается перед отрицательными значениями координат на оси ординат. На оси абсцисс номер зоны не указывается. Указание номера означает смещение нулевой отметки на 500 км в левую сторону. Это сделано, чтобы исключить наличие значений со знаком минус на карте.

Значения обозначаются в километрах и равны они промежутку от нулевой отметки на оси до соответствующего места на карте.

Значение при этом указывается двояко:

1. Полные координаты – указывается промежуток с точностью до метра.
2. Сокращённые координаты – обозначаются лишь километры до десятков и метры.

Однако в основном используются полные координаты, так как точное указание местоположения точки имеет большое значение в топографических целях. Сокращённые координаты допускается использовать лишь в случае, когда топографическая карта охватывает не более 10 тысяч квадратных километров, т. е. реальные длины осей не превышают ста километров.

При обозначении отрицательного значения на оси У указывается сначала ось, потом номер зоны по системе Гаусса и в конце промежуток от нулевой отметки до объекта на карте. Примерно, прямоугольные координаты точки на топографической карте выглядят следующим образом: х = 5 650 450; у = 3 620 840.

В подобном случае значение по оси Х толкуется прямо, а для установления отдалённости точки по ординате от нулевой отметки из указанного значения вычитается 500 километров. А это значит, что точка в указанном примере находится в 5 650 километрах и 450 метрах от экватора и 120 километрах и 840 метрах от срединного меридиана.

Определение точек на карте по координатной сетке

Координатную сеть иначе ещё называют километровой, так как на мелких картах величина квадратов сетки равняется километру. На подобных картах километровая сеть изображается в виде линий, прочерченных параллельно осями и имеющих определённый интервал между собой. Интервал устанавливается в зависимости от масштаба.

Так, при масштабе 1 : 25 000 значение интервала равняется 4 сантиметрам. При большем масштабе интервал не бывает меньше 2 сантиметров, невзирая на реальное расстояние между линиями. При масштабе больше чем 1 : 500 000 сетка прямо не изображается. Обозначаются лишь выходные метки по краям карты.

Координатная сеть является условной для отдельной зоны, и для сопоставления топографии соседних зон по краям карты оставляются отметки сетки, которые соответствуют выходам сетки соседней зоны.

При обозначении значений координат на топографических картах координатная сеть позволяет быстрее обозначить необходимую точку. Отсчет расстояния идёт от границ квадрата координатной сетки. Каждая из сторон отдельного квадрата сетки имеет заранее определенную реальную длину в километрах (1, 2 и т. д. километров).

Определение прямоугольных координат на топографической карте

Чтобы осуществить определение координат точек на картах, очень важно иметь ориентиры. Если изначальное координаты ясны и нужно лишь указать их на карте, то делается это следующим образом:

1. Определяется квадрат на сетке по километру координат.
2. При помощи линейки отсчитываются метровые величины внутри квадрата, сначала по параллельной линии к оси абсцисс, затем к оси ординат.
3. Вдоль линий указываются метровые значения.

В целом процедура завершена. Однако на практике не всё так просто. Зачастую не имеется значения изначальных координат. В таких случаях важно иметь определенные ориентиры, без которых найти точку представляется невозможным. В качестве ориентира может послужить любая близлежащая точка с известными координатами. Достаточно выяснить реальное расстояние между известной точкой и искомым объектом.

Указать адрес точки на карте на 100 % точно невозможно, так что определяются примерные значения.

С другой стороны, современные технологии позволяют произвести точные измерения на месте с моментальным отображением результатов на электронной топографической карте. Для этого применяются методы лазерного измерения или радиолокации. В любом случае при практической необходимости выяснения местоположения того или иного объекта недвижимости правильным решением будет обратиться к специалистам.

В качестве специалистов могут выступать:

• инженеры государственной службы геодезии и картографии (кадастр);
• специалисты частных инженерных служб.

При этом частные инженерные службы в своём распоряжении имеют более высокотехнологичное, а значит и более точное оборудование, нежели государственные органы. Разумеется, услуги таких специалистов стоят не дёшево.

Соотношение прямоугольных координат с другими системами обозначения точек на карте

Помимо непосредственного использования прямоугольной системы или системы Гаусса часто возникает необходимость сопоставления данных в указанной системе и на обычной географической карте. В таких случаях используется несколько методов:

1. Метод перевода значения из числового значения в стандартные значения (широты и долготы).
2. Способ наложения значения расстояний по масштабу.
3. Метод сопоставления географической карты с целой зоны Гаусса.

Практическое применение находит лишь первый метод, так как он признан официальным способом переложения координат объектов недвижимости из обычной топографической карты в географическую. Именно данный способ используют государственные службы и частные специалисты.

С другой стороны, это один из самых сложных способов, требующий специальных навыков и знаний. Кроме того необходимо наличие сведений о ключевых топографических точках.

Самым простым способом признаётся метод наложения расстояния. По сути, зная масштаб, вычислить координаты может даже школьник при помощи обычной линейки. Однако погрешность в таком случае может быть равна десяткам километров.

Метод сопоставления карт применяется крайне редко. К примеру, такой способ может быть использован при корректировке генерального плана расширения населённых пунктов, определения границ регионов и государств.

Но данные методы позволяют не только решить частные проблемы, но и узнать координаты искомого объекта недвижимости. Такое стало возможным после предоставления открытого доступа к картам GPS. Постоянное спутниковое наблюдение за поверхностью земли позволило с точностью до метра определить местоположение практически любого объекта, не оснащенного радиопоглощающим покрытием.

Выяснить местоположение путем сопоставления данных с GPS и топографической карты может практически любой человек. Для этого необходимо:

• получить данные географических координат из системы GPS, выраженные в широте и долготе;
• по ним вычислить зону Гаусса (срединный меридиан в зоне);
• переложить точку соответственно зоне Гаусса.

Разумеется, задача не простая, но зато выполнимая. Другой вопрос – официальный статус такого вычисления.

Официальный статус определённых прямоугольных координат объектов недвижимости

Выявленные частным образом координаты никогда не будут иметь официального статуса. Ведь в целях топографии законодательством установлены специальные ГОСТы определения местоположения объектов недвижимости. Но при желании одним из вышеуказанных способов можно проверить соответствие официальных данных по тому или иному объекту недвижимости.

Очень редко, но всё же встречаются случаи, когда официальные данные в службе геодезистов не совсем точны. Никакого практического значения в повседневной жизни данный фактор может и не иметь. Однако он важен при определении так называемых «красных линий» на топографических картах. Это линии, по которым будут пролегать дороги и инженерные линии, и которые будут в будущем реквизированы.

Если по топографической карте данные объекта недвижимости указаны неверно, то его владелец может оказаться жертвой ошибочной реквизиции. Чтобы такого не случилось, при выявлении несоответствий фактических и официальных топографических координат необходимо сообщить об этом в уполномоченный орган (кадастр).

Если в удовлетворении ходатайства о проведении проверки и внесении изменений служба откажет, то можно добиться своего через суд. В таком случае будет назначена отдельная экспертиза с привлечением сторонних специалистов. В целом, процедура расходная и отнимает много времени, но рано или поздно владелец недвижимости может с таким столкнуться.

Источник