Способ прямоугольного треугольника
Способ прямоугольного треугольника является одним из тех методов в котором находится действительная величина отрезка или расстояние между двумя точками прямой по двум проекциям. В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.
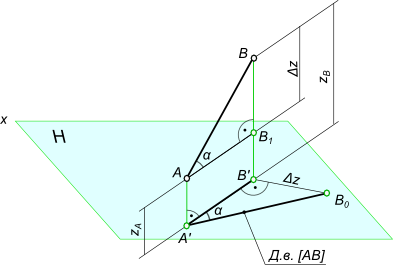
Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB1) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций.
Для определения натуральной величины отрезка прямой общего положения и углов наклона ее к плоскости проекций на КЧ необходимо построить прямоугольный треугольник: — первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов); — из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций; — гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка.
Ортогональная проекция отрезка общего положения всегда будет меньше его действительной величины.
Для графического определения на эпюре Монжа действительной величины отрезка или расстояния между двумя точками прямой может быть использован способ прямоугольного треугольника. Где выполняется построение прямоугольного треугольника: — за один его катет принимается горизонтальная (фронтальная, профильная) проекция отрезка; — а за другой катет — разность удаления концов отрезка от горизонтальной (или соответственно фронтальной, профильной) плоскости проекции; — гипотенуза, полученного таким образом, прямоугольного треугольника равна действительной величине заданного отрезка или расстояния между двумя точками прямой.
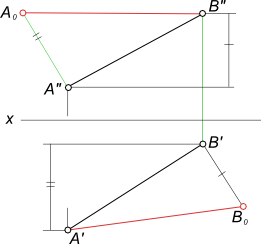
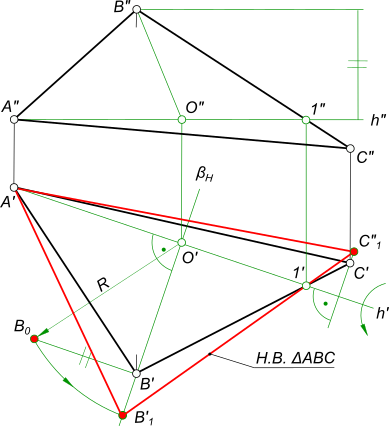
Графическое определение действительной величины отрезка [AB] или расстояния между двумя точками прямой A и B путем построения прямоугольных треугольников ΔA`B`B0 или ΔA»B»A0.
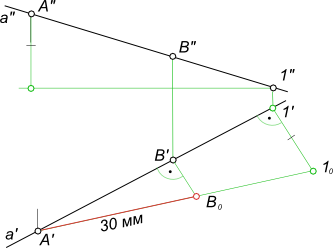
Используя способ прямоугольного треугольника, можно также решать задачу по построению на эпюре: — проекции отрезка, наперед заданной величины; — проекции расстояния между двумя точками прямой, наперед заданной величины.
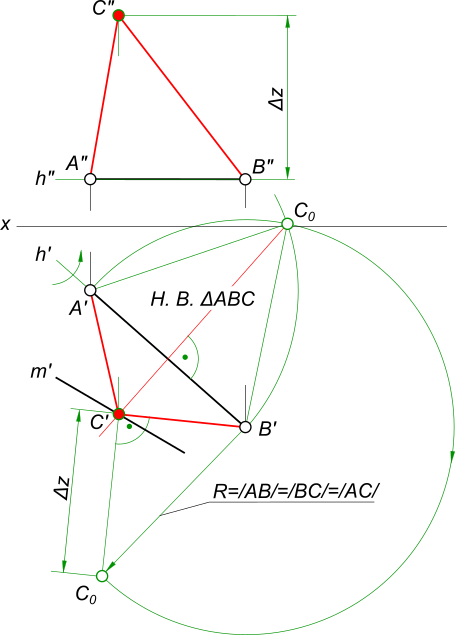
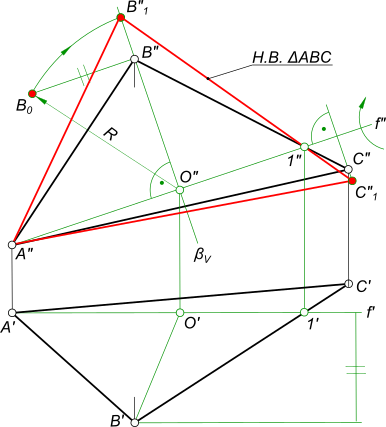
Даны проекции равностороннего треугольника ABC(A`B`C`,A»B». ) .
Построить недостающие проекции треугольника.
Построение равностороннего треугольника выполняется с использованием способа прямоугольного треугольника
Другие графические способы определение действительной величины, натурального вида или натуральной величины отрезка, плоской фигуры изложены в статье: Метод преобразования. Определение действительной величины треугольника ΔABC показаны на примере решения двух задач в статье: Графическая работа 3
Способ прямоугольного треугольника применяется в статье графическая работа 1: Графическая работа 1
Если вы искали не Способ прямоугольного треугольника а: Проекции треугольника, нажмите на ссылку.
Построение треугольника в плоскости общего положения смотри: Вращение вокруг следа
Источник
Определение натуральной величины отрезка
Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.
Метод прямоугольного треугольника
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.
Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A0A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A0 равен величине ZA – ZB, то есть разности удаления точек A и B от горизонтальной плоскости П1.
Откладываем A’A0 = ZA – ZB перпендикулярно A’B’. Затем проводим гипотенузу A0B’ треугольника A0A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.
Способ параллельного переноса
Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П1, то длина его проекции E’F’ не изменится, когда она займет новое положение E’1F’1 (как это показано на рисунке ниже).
Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.
Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’1F’1 = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»1 и F»1. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.
Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.
Поворот вокруг оси
Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.
Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’1N’1, параллельное оси X.
По линиям связи находим точку M»1. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.
Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»1 и M»1 искомым отрезком. На рисунке он выделен красным цветом.
Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.
Источник
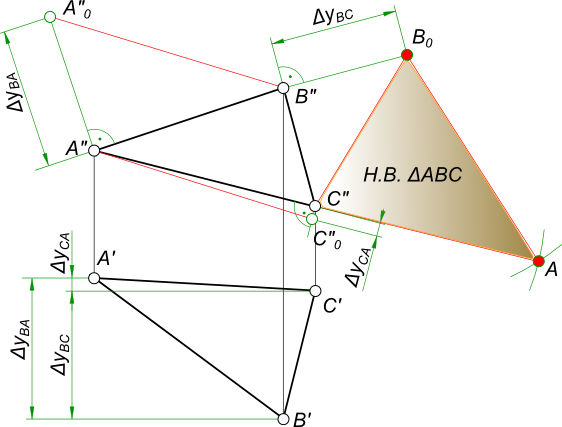
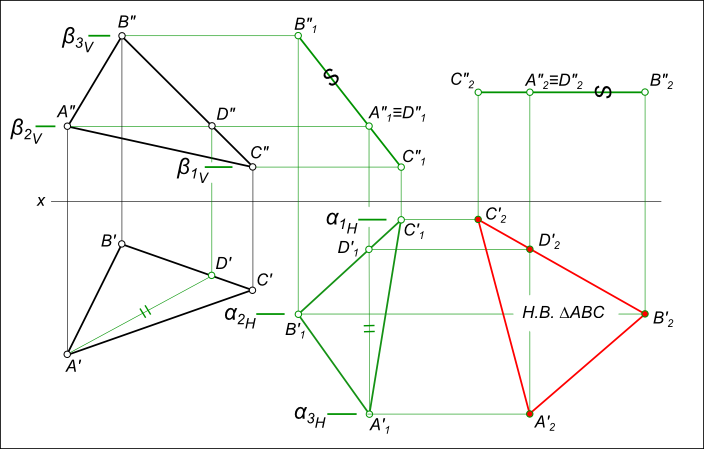
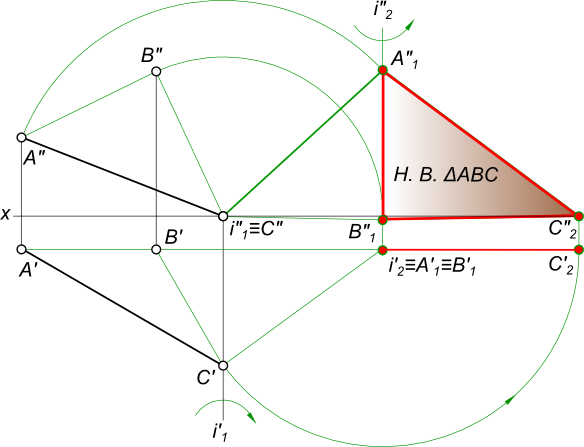
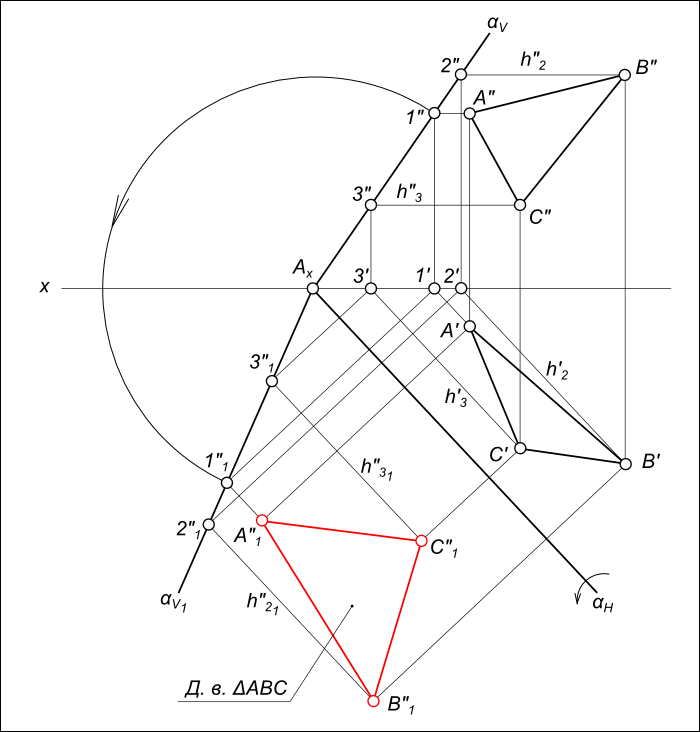
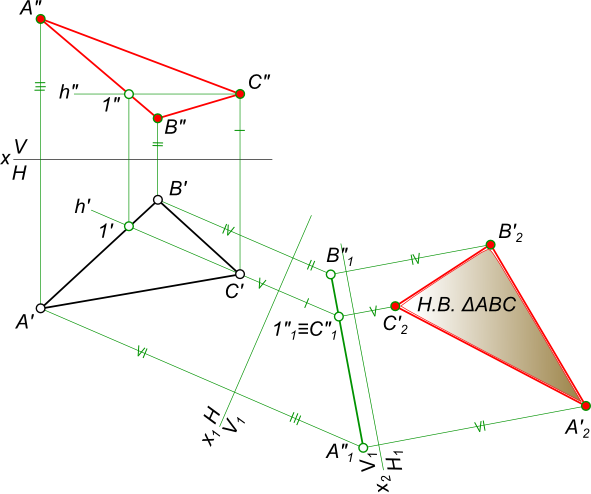
Натуральная величина треугольника
Натуральная величина треугольника на эпюре Монжа может быть определена: — способом прямоугольного треугольника;
Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.
Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:
— Способ вращения вокруг осей перпендикулярных плоскостям проекций;
— Вращение вокруг горизонтали представляющих собой линии уровня;
представляющих собой линии уровня;
— Вращение вокруг следа или способ совмещения с плоскостью проекций;
Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.
Источник
Способ прямоугольного треугольника



Рисунок 30
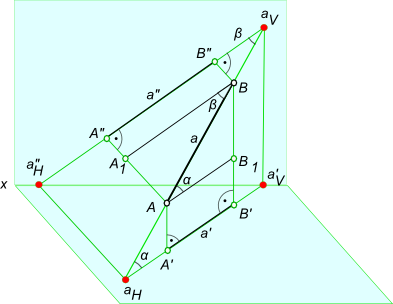
Этот способ применяется для определения натуральных величин отрезков общего положения, а также углов наклона их к плоскостям проекций. Для того, чтобы определить натуральную величину отрезка этим способом, необходимо достроить прямоугольный треугольник к одной из проекций отрезка. Другим катетом будет являться разность высот или глубин конечных точек отрезка, а гипотенуза – натуральной величиной.
Рассмотрим пример: на рисунке 31 дан отрезок АВ общего положения. Требуется определить его натуральную величину и углы его наклона к фронтальной и горизонтальной плоскостям проекций.
Проводим перпендикуляр к одному из концов отрезка на горизонтальной плоскости. Откладываем на нем разность высот (ZA-ZB) концов отрезка и достраиваем прямоугольный треугольник. Гипотенуза его является натуральной величиной отрезка, а угол между натуральной величиной и проекцией отрезка – натуральной величиной угла наклона отрезка к плоскости П1. Порядок построений на фронтальной плоскости тот же самый. По перпендикуляру откладываем разность глубин концов отрезка (YA-YB). Полученный угол между натуральной величиной отрезка и его фронтальной проекцией – это угол наклона отрезка к плоскости П2.
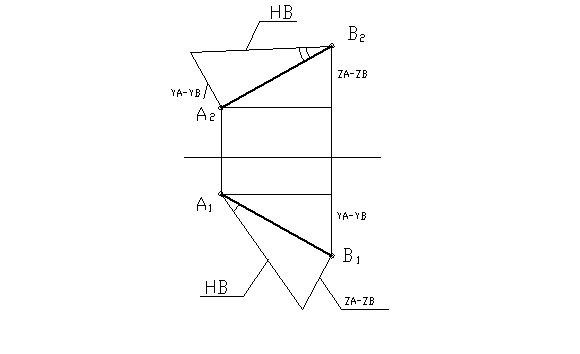
Рисунок 31
1. Сформулируйте теорему о свойстве прямого угла.
2. В каком случае прямая перпендикулярна плоскости ?
3. Сколько прямых и сколько плоскостей, перпендикулярных данной плоскости, можно провести через точку пространства ?
4. Для чего применяется способ прямоугольного треугольника ?
5. Как при помощи этого способа определить угол наклона отрезка общего положения к горизонтальной плоскости проекций ?
Источник
Определение натуральной величины прямой
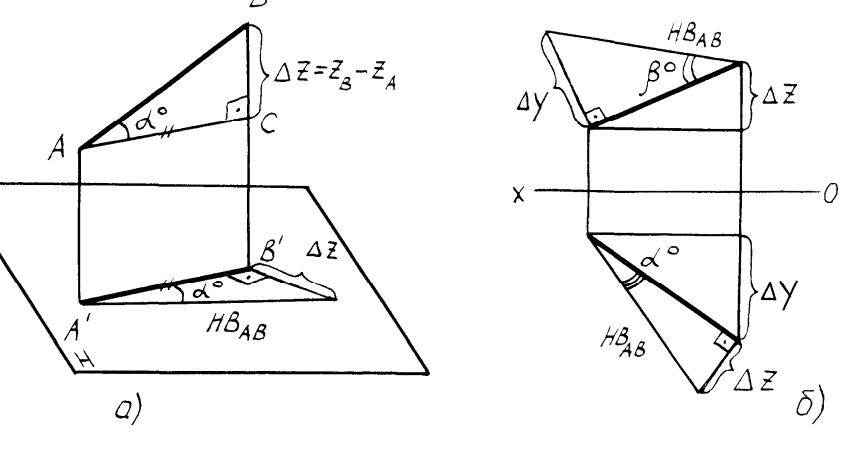
Так как прямая общего положения проецируется на плоскости проекций с искажением, то задача определения натуральной величины (НВ) прямой по её проекциям является важной. С целью определения НВ прямой разработан метод прямоугольного треугольника, сущность которого понятна из пространственного чертежа (рисунок 2.4а). Для того, чтобы определить натуральную величину прямой по её проекциям, необходимо на одной из её проекций (на любой) построить прямоугольный треугольник, одним катетом которого является сама проекция, а другим катетом– разность недостающих координат концов отрезка прямой. Тогда гипотенуза треугольника будет являться НВ прямой (рисунок 2.4б). Недостающей координатой здесь названа та координата, которая не участвует в построении той или иной проекции прямой. Так, например,горизонтальная проекция прямой строится по координатам X и Y её концов. Координата Z в построениях не участвует и называется недостающей координатой. Таким образом, при построении прямоугольного треугольника на горизонтальной проекции прямой на катете откладывают разность аппликат, а при построении на фронтальной проекции – разность ординат. При определении НВ прямой методом прямоугольного треугольника одновременно можно определить углы наклона прямой к плоскостям проекций (углы αο и βο). Они определятся как углы между гипотенузой и соответствующей проекцией прямой.
Рисунки 2.4 – Метод прямоугольного треугольника
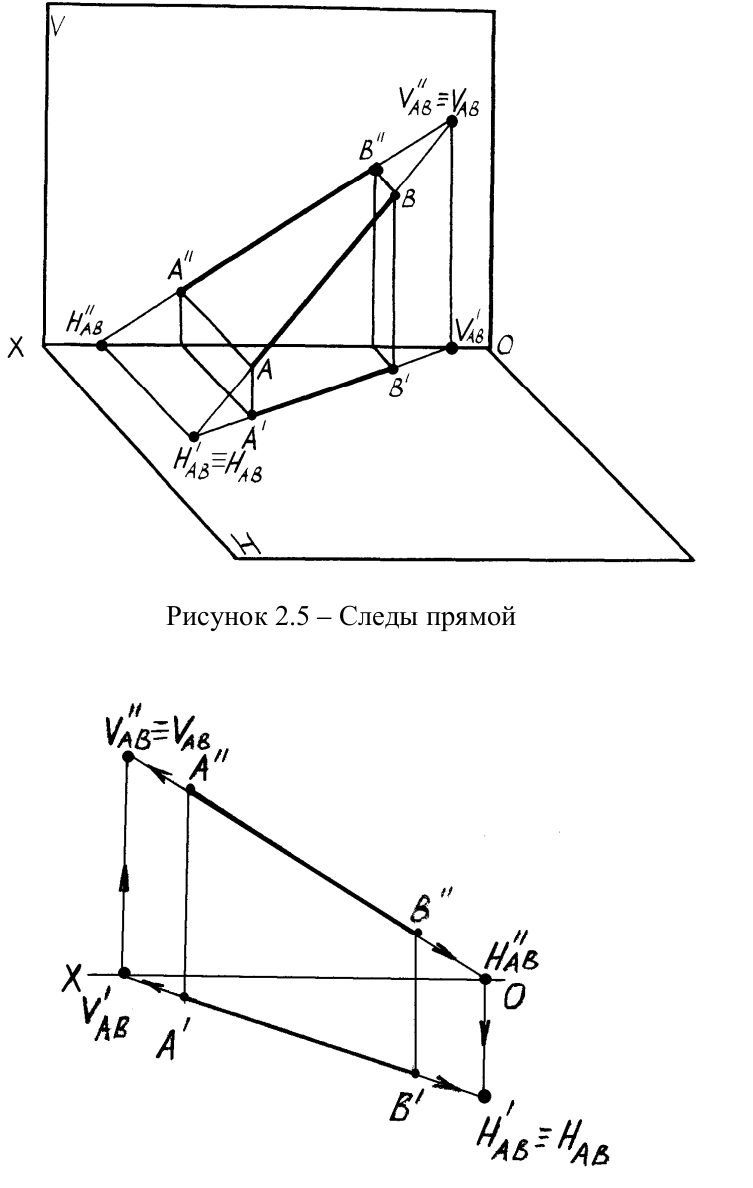
Следы прямой
Точки пересечения прямой с плоскостями проекций называются следами прямой. В точках следов прямая переходит из одного октанта в другой. Различают горизонтальный, фронтальный и профильный следы прямой и их соответствующие проекции. На рисунке 2.5 показаны пространственные чертежи прямых общего и частного положения и образование их следов. Прямые, параллельные плоскостям проекций, имеют только два следа, а прямые, перпендикулярные плоскостям проекций, — один след, совпадающий с той проекцией прямой, на которой она проецируется в точку.
Рисунок 2.5 – Следы прямой
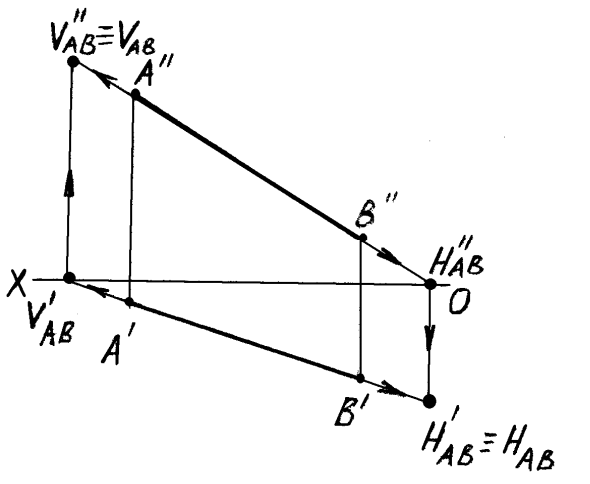
Рисунок 2.6 – Построение следов прямой
Из пространственных чертежей следует методика построения проекций следов прямой на эпюре (рисунок 2.6).
Источник