Определение натуральной величины отрезка
Если отрезок параллелен плоскости, то он проецируется на неё без искажений. В остальных случаях для нахождения его натуральной величины применяют метод прямоугольного треугольника или способы преобразования ортогональных проекций.
Метод прямоугольного треугольника
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.
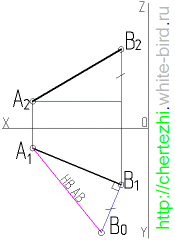
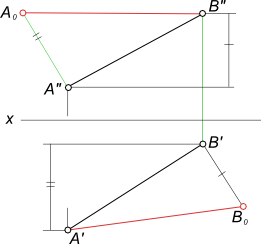
Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A0A’B’. Его первый катет A’B’ – это горизонтальная проекция AB. Второй катет A’A0 равен величине ZA – ZB, то есть разности удаления точек A и B от горизонтальной плоскости П1.
Откладываем A’A0 = ZA – ZB перпендикулярно A’B’. Затем проводим гипотенузу A0B’ треугольника A0A’B’. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.
Способ параллельного переноса
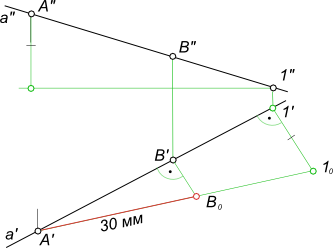
Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Например, если перемещать отрезок EF параллельно горизонтальной плоскости П1, то длина его проекции E’F’ не изменится, когда она займет новое положение E’1F’1 (как это показано на рисунке ниже).
Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X.
Чтобы определить действительный размер отрезка EF, на свободном месте чертежа строим его новую горизонтальную проекцию E’1F’1 = E’F’ так, чтобы она была параллельна оси X . Затем по линиям связи находим точки E»1 и F»1. Расстояние между ними и есть искомая величина, поскольку мы перенесли EF в положение, параллельное фронтальной плоскости.
Метод параллельного переноса, описанный здесь, иногда называют параллельным перемещением. Посмотреть дополнительные примеры и получить более подробную информацию по данной теме можно в этой статье.
Поворот вокруг оси
Для того, чтобы отрезок стал параллелен плоскости проекции и без искажения отразился на ней, он может быть повернут вокруг проецирующей прямой, проходящей через один из его концов.
Определим длину произвольного отрезка MN. Для этого через точку N проводим горизонтально проецирующую прямую i. Вокруг неё поворачиваем MN так, чтобы его проекция M’N’ заняла положение M’1N’1, параллельное оси X.
По линиям связи находим точку M»1. При этом исходим из того, что M» в процессе вращения движется параллельно горизонтальной плоскости.
Точка N не изменит своего положения, так как лежит на оси поворота. Поэтому осталось только соединить N»1 и M»1 искомым отрезком. На рисунке он выделен красным цветом.
Более подробную информацию о решении задач методом поворота вокруг оси вы можете получить, ознакомившись со следующим материалом.
Источник
Способом прямоугольного треугольника можно определить натуральную величину

Как определить натуральную величину отрезка?

************************ —>
Сегодня мы рассмотрим один из самых простых элементов теории, но важность его такова, что без него решение большинства задач по начертательной геометрии не представляется возможным. Если вы не знаете, как определить натуральную величину отрезка, то вы никогда не сможете доказать преподавателю, что решили задачи самостоятельно. Задача на определение натуральной величины отрезка в начертательной геометрии встречается как сама по себе, так и в качестве вспомогательных построений при решении сложных комплексных задач. В любом случае, каждый студент, который планирует получить зачет\экзамен по начерталке, обязан уметь определить натуральную величину отрезка, причем быстро и без заминок.
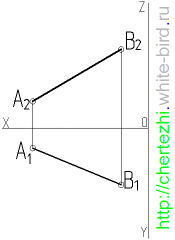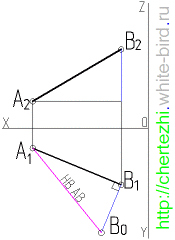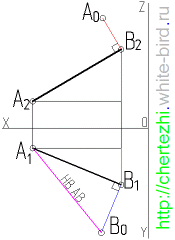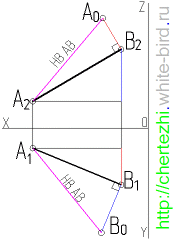
Имея две проекции прямой частного положения мы всегда можем определить натуральную величину любого отрезка отложенного на этой прямой. Для этого используется метод прямоугольного треугольника. На рисунке в начале статьи мы определили натуральную величину отрезка АВ построив прямоугольный треугольник на горизонтальной плоскости проекции, но вы должны знать, что построить прямоугольный треугольник мы можем как на горизонтальной, так и на фронтальной плоскостях. Это показано на анимированном рисунке ниже — на нем мы сначала определили натуральную величину АВ на горизонтальной плоскости проекции, а затем на фронтальной
Коротко же алгоритм определения натуральной величины отрезка сводится следующему: на любой проекции через любую из конечных точек отрезка проводят перпендикулярную прямую, и на ней откладывают расстояние, равное разнице значений по оси ординат этих двух точек на противоположной плоскости проекций. Т.е. если треугольник строим на горизонтальной плоскости, то разницу значений ищем на фронтальной, и наоборот. Если что-то непонятно из этого описания, то рассмотрев внимательно рисунок вы окончательно поймете, что имелось ввиду.
Как видите, ничего особо сложного в этом приеме нет, но знать его очень важно, и не менее важно уметь его применить, как минимум до получения зачета по начертательной геометрии и инженерной графике 🙂
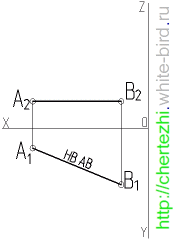
Особым случаем этой задачи является определение натуральной величины отрезка лежащего в частном положении — например параллельно горизонтальной плоскости проекции. Тогда на его горизонтальная проекция будет сама по себе натуральной величиной и никаких дополнительных построений для ее определения не требуется:
Внимание! Для этой темы есть видеоурок.
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.
А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны: 
Автор комментария: Олечка
Дата: 2012-10-02
Автор комментария: Санша
Дата: 2012-12-27
Автор комментария: антон
Дата: 2012-12-28
спасибо) все понял за 10сек)
Автор комментария: иван
Дата: 2013-01-12
Спасибо Вам. Чтобы я без вас делал
Автор комментария: Кондрат
Дата: 2013-02-18
Спасибо большое,всё понятно!)
Автор комментария: Андрей
Дата: 2013-02-26
Автор комментария: amik0
Дата: 2013-06-06
Спасибо, наконец-то понятно.
Автор комментария: Cережа
Дата: 2013-09-07
Спасибо огромное:) все ясно и понятно:)
Автор комментария: жанна
Дата: 2013-09-23
СПАСИБО. Я наконец то поняла!думаю сдам без косяков.
Всегда хотел донести до молодого поколения основы, которые отчего-то не могут донести штатные преподаватели. Успехов в учебе, всем сказавшим «спасибо»! А также и тем кто забыл сказать, но понял тему!
Автор комментария: Евгений
Дата: 2013-12-19
Спасибо. Наконец-то понял. Удачи завтра мне.
Автор комментария: леха
Дата: 2014-01-08
Автор комментария: Евгений
Дата: 2014-01-22
Автор комментария: Лезгистан
Дата: 2014-01-28
спасибо большое,сразу понял
Автор комментария: Дариус
Дата: 2014-09-21
Спасибо, очень помогло
Автор комментария: Кофе
Дата: 2014-09-24
Спасибо. Я все понял, и теперь я успешный дотер, который не пошел в армию, потому что все сдал.
Автор комментария: Даня
Дата: 2014-09-28
Спасибо, все понял, а как на третьем виде строить? или там нельзя?
Автор комментария: Максим
Дата: 2014-10-21
Автор комментария: Леша
Дата: 2014-10-26
Автор комментария: Светлана
Дата: 2014-11-26
Автор комментария: алтынай
Дата: 2015-10-01
Забегайте! Тут еще много полезного:)
Автор комментария: Диана
Дата: 2015-10-04
Спасибо огромное! Очень доступно и понятно
Диана, спасибо вам за желание разобраться! Удачи!
Автор комментария: Ася
Дата: 2015-10-10
Просто спасли!Огромное спасибо!
Ну. Примерно для этого я все это и пишу:) удачи!
Автор комментария: Евгений
Дата: 2015-10-15
Автор комментария: Никита
Дата: 2015-11-04
Спасибо огромное, очень хорошее поясняющее видео!)
Автор комментария: Лёва
Дата: 2015-12-14
Автор комментария: Nitisha
Дата: 2016-01-06
спасибо большое, обьяснения очень хорошие .
Автор комментария: Алиса
Дата: 2016-01-19
Спасибо вам огромное
Автор комментария: Викус
Дата: 2016-04-14
Всё доступно и понятно. Спасибо. Особенно за анимашку)
Автор комментария: Данил
Дата: 2016-09-21
Спасибо большое! Всё объяснено просто и главное понятно!
Автор комментария: Alex
Дата: 2016-10-23
Автор комментария: егор
Дата: 2016-11-03
Автор комментария: Алексей
Дата: 2016-11-10
Группа ЭМ-36у благодарит вас за простое и понятное обьяснение
Автор комментария: Никита
Дата: 2016-11-10
Согласен с предыдущим оратором!
Приветы всем, кто хочет сам разобраться в предмете! Ищите меня во Вконтакте — ссылка в правом столбике выше. Подписывайтесь, вступайте в группу, будет нескучно и полезно для домашних заданий! Покуда вы будете в этом заинтересованы — совершенно бесплатно! Уникально, так сказать 🙂
да-да-да. А кто это тут у нас конспекты не ведёт? Алексей и Никита, да?!
Мужики, ну вы даете 🙂 И прекрасные дамы!
Автор комментария: Сергей
Дата: 2017-01-11
https://vk.com/XXXX_XXXX — чертежи — 3D-модели — оцифровка чертежей — чертежи для студентов — выполнение чертежей по фото, эскизам и деталям — разработка чертежей на оснастку и металлоконструкции Разрабатываем чертежи в г. Гомель. Начертательная геометрия и инженерная графика для учебных заведений Гомеля и не только. Другие услуги актуальны для города Гомель. Работы выполняются карандашом, в программах КОМПАС-3D, AutoCAD, SolidWorks. Возможно сохранение в других популярных форматах.
Сергей, предложите мне что-нибудь выгодное. И ваша ссылка сможет жить здесь до скончания проекта 🙂
Автор комментария: фахри
Дата: 2017-10-17
Источник
Способ прямоугольного треугольника
Способ прямоугольного треугольника является одним из тех методов в котором находится действительная величина отрезка или расстояние между двумя точками прямой по двум проекциям. В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.
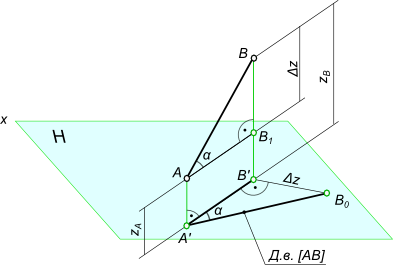
Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB1) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций.
Для определения натуральной величины отрезка прямой общего положения и углов наклона ее к плоскости проекций на КЧ необходимо построить прямоугольный треугольник: — первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов); — из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций; — гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка.
Ортогональная проекция отрезка общего положения всегда будет меньше его действительной величины.
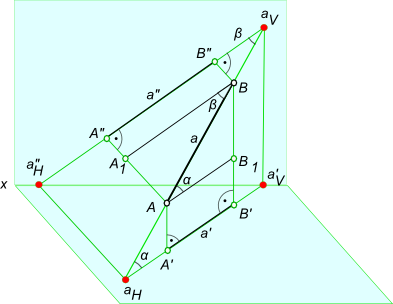
Для графического определения на эпюре Монжа действительной величины отрезка или расстояния между двумя точками прямой может быть использован способ прямоугольного треугольника. Где выполняется построение прямоугольного треугольника: — за один его катет принимается горизонтальная (фронтальная, профильная) проекция отрезка; — а за другой катет — разность удаления концов отрезка от горизонтальной (или соответственно фронтальной, профильной) плоскости проекции; — гипотенуза, полученного таким образом, прямоугольного треугольника равна действительной величине заданного отрезка или расстояния между двумя точками прямой.
Графическое определение действительной величины отрезка [AB] или расстояния между двумя точками прямой A и B путем построения прямоугольных треугольников ΔA`B`B0 или ΔA»B»A0.
Используя способ прямоугольного треугольника, можно также решать задачу по построению на эпюре: — проекции отрезка, наперед заданной величины; — проекции расстояния между двумя точками прямой, наперед заданной величины.
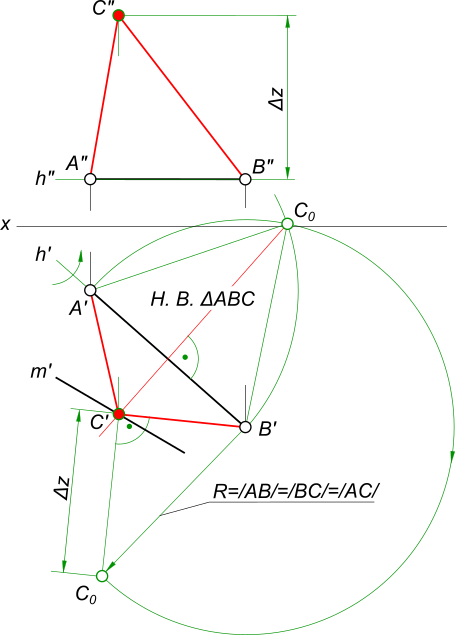
Даны проекции равностороннего треугольника ABC(A`B`C`,A»B». ) .
Построить недостающие проекции треугольника.
Построение равностороннего треугольника выполняется с использованием способа прямоугольного треугольника
Другие графические способы определение действительной величины, натурального вида или натуральной величины отрезка, плоской фигуры изложены в статье: Метод преобразования. Определение действительной величины треугольника ΔABC показаны на примере решения двух задач в статье: Графическая работа 3
Способ прямоугольного треугольника применяется в статье графическая работа 1: Графическая работа 1
Если вы искали не Способ прямоугольного треугольника а: Проекции треугольника, нажмите на ссылку.
Построение треугольника в плоскости общего положения смотри: Вращение вокруг следа
Источник