Способом плоскопараллельного перемещения найти нв треугольника авс

Плоскопараллельное перемещение треугольника

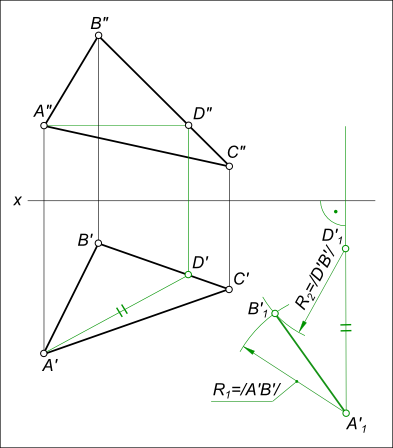
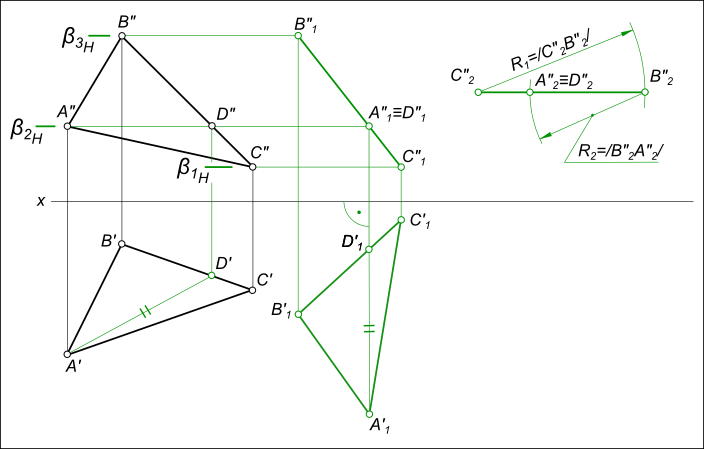
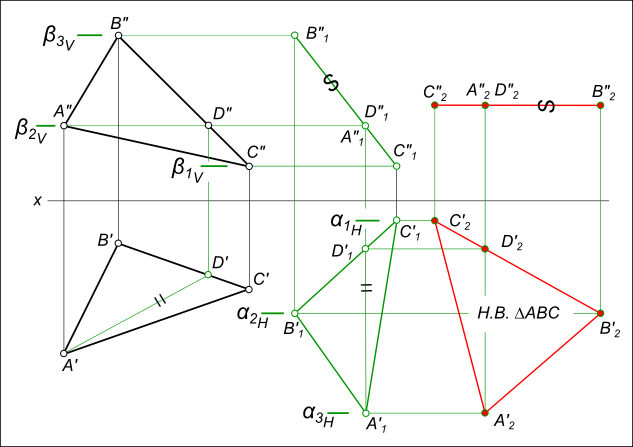
Плоскопараллельное перемещение треугольника ΔABC используемое для преобразования его ортогональных проекций, соответствующих плоскости общего положения δ, в проекции δ₂ // H для получения натуральной величины сторон и углов треугольника ΔABC требует выполнения следующих построений: — горизонтали (или фронтали) плоскости AD;

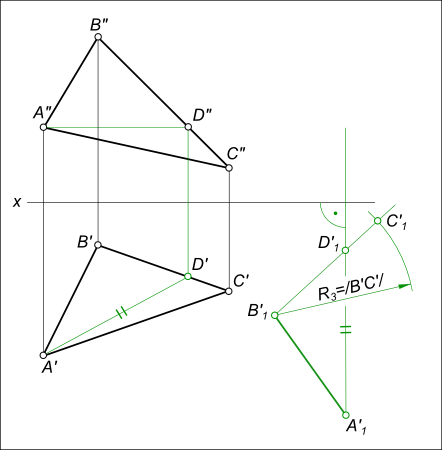
— перевода горизонтали плоскости в положение A₁D₁ ⊥ V: — на направлении перпендикуляра к плоскости V проведенном на свободном месте чертежа откладываем величину A`D` = A`<sub>1</sub>D`₁ — перестроение других точек проекции ΔA`B`C` на новое положение ΔA`₁B`<sub>1</sub>C`₁: — точку B`<sub>1</sub> дает пересечение дуг R<sub>1</sub> = /A`B`/ и R<sub>2</sub> = /D`B`/; — сторону B`D` продолжим до пересечения

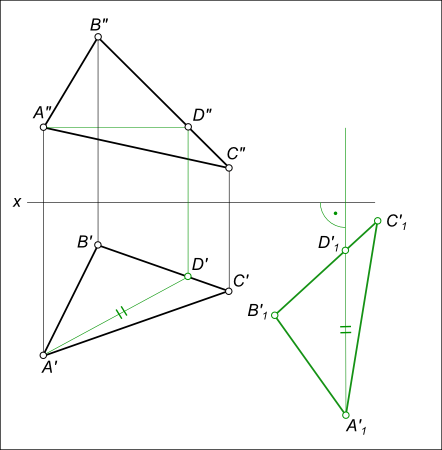
с дугой радиуса R₃ = /B`C`/; — проекции вершин треугольника в новом положении соединяем прямыми линиями;

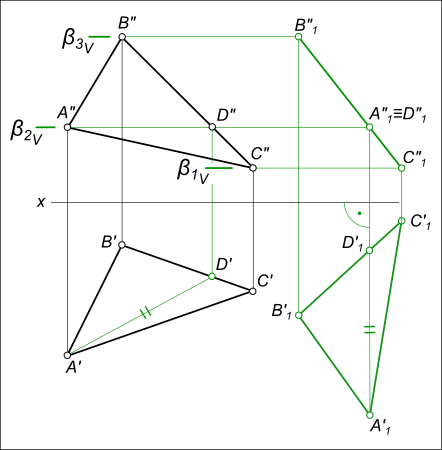
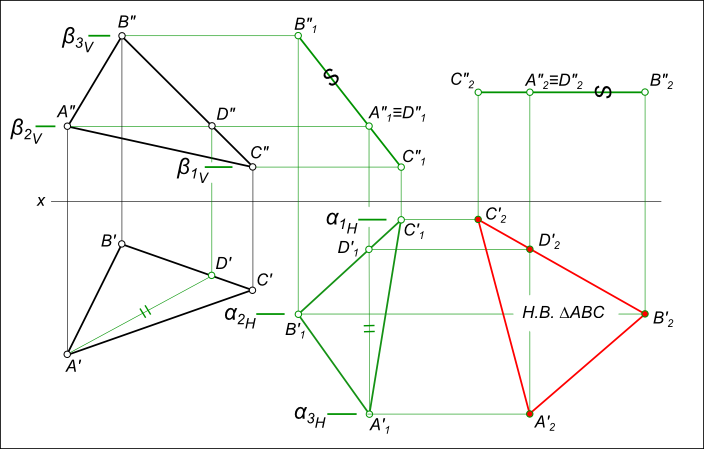
— перемещения фронтальных проекций ΔA»B»C» к новому положению ΔA»₁B»₁C»₁, происходящего в плоскостях уровня β1_V, β2_V и β3_V параллельных плоскости H;

— новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи; — перемещения фронтальной проекции ΔA»₁B»₁C»₁ в положение параллельное H,

которое выполняем переводом прямой В»₁С»₁ — фронтальной проекции ΔA₁B₁C₁ в положение параллельное оси x: В»₂С»₂ // x; — перемещения горизонтальных проекций ΔA`<sub>1</sub>B`₁C`<sub>1</sub> к новому положению ΔA`₂B`<sub>2</sub>C`₂, происходящего в плоскостях уровня α1_H, α2_H и α3_H параллельных плоскости V;

— новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи: проекция ΔA`<sub>2</sub>B`₂C`₂ соответствует натуральной величине треугольника ΔABC.

Источник

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения (переноса) имеет справедливым утверждение, которое может быть выражено в виде следующей теоремы.

При параллельном переносе геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.

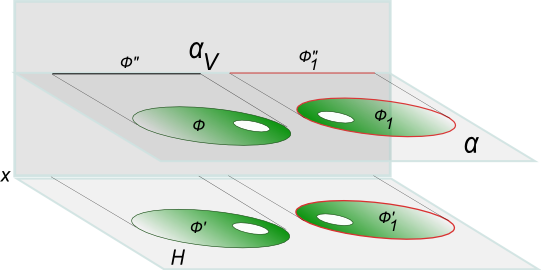
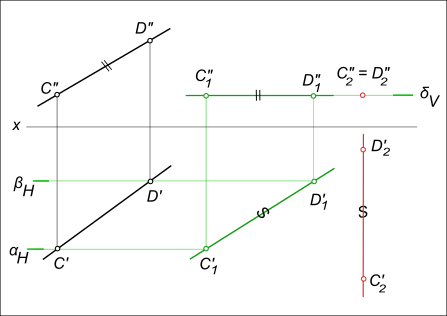
Докажем эту теорему для случая, когда проецируемая фигура Ф плоская, и ее плоскость принадлежит плоскости уровня Ф⊂α, плоскость α║H (рисунок). В этом случае, на основании свойства 6 ортогонального проецирования горизонтальная проекция Ф` будет конгруентна самой фигуре Ф(Ф`≅Ф).

При перемещении фигуры Ф в новое положение Ф₁, фигура Ф`₁ будет конгруентна Ф, так как:

а) расстояние между точками фигуры не меняется;

б) в процессе перемещения фигура Ф все время остается в плоскости α.

В силу параллельности плоскостей α и H, Ф`<sub>1</sub>≅Ф<sub>1</sub>, но Ф<sub>1</sub>≅Ф, а Ф≅Ф`, следовательно Ф`<sub>1</sub>≅Ф`. Данная теорема будет справедлива и в случае, когда геометрическая фигура занимает произвольное (непараллельное) положение относительно плоскости проекции.

а) При всяком перемещении точки в плоскости, параллельной плоскости проекции H, ее фронтальная проекция перемещается по прямой, параллельной оси x.

б) В случае произвольного перемещения точки в плоскости, параллельной V, ее горизонтальная проекция перемещается по прямой, параллельной оси x.

Пользуясь теоремой и отмеченными свойствами, не составляет труда построить новые проекции геометрической фигуры (по заданным ее ортогональным проекциям), которые соответствуют частным положениям проецируемой фигуры по отношению к плоскости проекции.

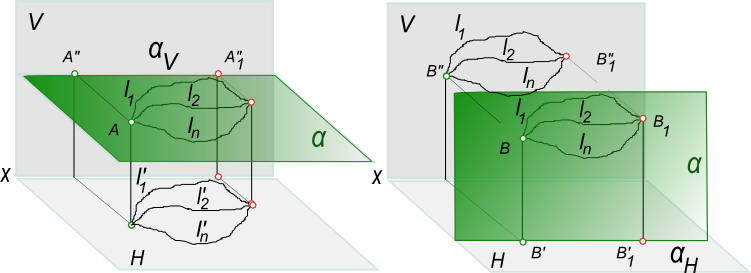
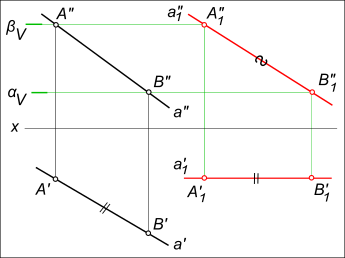
[AB]- отрезок прямой а общего положения перевести в положение параллельное V. Выполняем перемещение отрезка [A`B`] на горизонтальной плоскости проекции в положение параллельное оси x [A₁B₁]. При таком перемещении новая горизонтальная проекция конгруентна исходной [AB]≅[A₁B₁] на основании теоремы.

Фронтальные проекции точек отрезка [A»B»] будут перемещаться в новое положение [A»₁B»₁] в плоскостях α и β параллельных горизонтальной плоскости проекции — по следам α_V и β_V.

Для перевода отрезка прямой общего положения в положение параллельное V требуется одно перемещение отрезка параллельно плоскости проекции H.

Для перевода отрезка прямой из общего положения в проецирующее, необходимо последовательно выполнить два перемещения параллельно плоскостям проекции.

Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проецирующее, можно легко перевести плоскость, произвольно расположенную в пространстве, в частное положение (параллельное или перпендикулярное плоскости проекции).

В графической работе №4 используется способ плоскопараллельного перемещения для решение задачи по построению треугольной пирамиды SABC: Графическая работа 4. В графической работе №5 используется способ плоскопараллельного перемещения для решение задачи по по определению наклона ребра SC треугольной пирамиды SABC к плоскости основания ABC: Графическая работа 5. Плоскопараллельное перемещение треугольника, со всеми подробностями, смотри: Плоскопараллельное перемещение треугольника

Источник

Плоскопараллельное перемещение

Плоскопараллельное перемещение

Частный случай способа вращения вокруг проецирующей оси — вращение предмета без указания на чертеже осей вращения, который называют способом плоскопараллельного перемещения. Способ удобен тем, что повернутые вокруг предполагаемой проецирующей оси проекции предмета перемещают и располагают на свободном поле чертежа без взаимного их наложения.

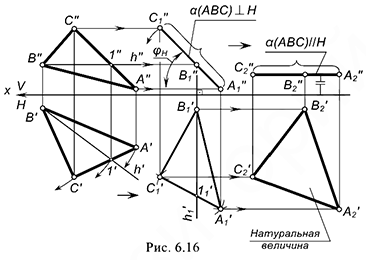
На рис. 6.16 показано построение натуральной величины плоскости общего положения, заданной треугольником 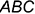, способом плоскопараллельного перемещения.

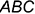
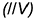
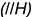
Для решения задачи плоскость должна занять положение плоскости уровня — или фронтальной или горизонтальной . Следовательно, плоскость нужно вращать и одновременно перемещать по полю чертежа, чтобы она последовательно заняла сначала проецирующее положение, а затем положение плоскости уровня.

Для двух последовательных преобразований нужно выполнить следующий графический алгоритм.

Первое перемещение. Плоскость общего положения вращением вокруг предполагаемой, например, горизонтально-проецирующей оси преобразовать во фронтально-проецирующую плоскость, выполнив следующие графические действия:

1-е действие. Провести в плоскости горизонталь .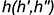

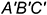
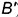
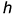
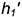
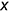
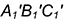
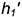
2-е действие. Повернуть горизонтальную проекцию треугольника, вращая вокруг предполагаемой горизонтально-проецирующей оси (например, проходящей через точку ) и одновременно перемещая вправо на свободное поле чертежа так, чтобы горизонталь плоскости заняла положение фронтально-проецирующей прямой, то есть должна расположиться перпендикулярно оси . Повернутую проекцию треугольника относительно проекции горизонтали построить с помощью дуговых засечек, на пересечении которых определяются вершины.

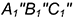
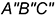
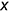
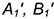
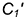
3-е действие. Построить фронтальную проекцию треугольника, переместив заданные фронтальные проекции вершин треугольника параллельно оси проекций до пересечения с вертикальными линиями связи от точек и повернутой проекции: фронтальная проекция выродилась в линию, то есть треугольник преобразовался во фронтально-проецирующую плоскость.

Второе перемещение. Плоскость фронтально-проецирующую вращением вокруг предполагаемой фронтально-проецирующей оси преобразовать в горизонтальную плоскость уровня, продолжая графические действия:

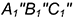
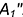
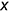
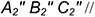
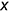
4-е действие. Повернуть построенную вырожденную проекцию треугольника, вращая вокруг предполагаемой фронтально-проецирующей оси, проходящей через точку , и одновременно перемещая вправо на свободное поле чертежа так, чтобы эта проекция расположилась параллельно оси проекций : проекция оси .

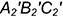
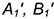
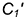
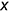
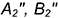
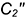
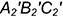
5-е действие. Построить новую горизонтальную проекцию треугольника, переместив горизонтальные проекции и вершин треугольника параллельно оси проекций до пересечения вертикальными линиями связи от фронтальных проекций и вершин; построенная горизонтальная проекция треугольника и есть его натуральная величина, так как после второго перемещения треугольник преобразовался в горизонтальную плоскость уровня.

Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник