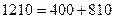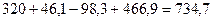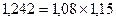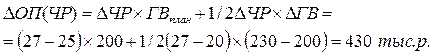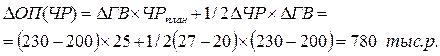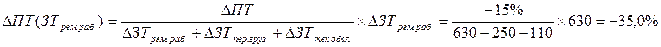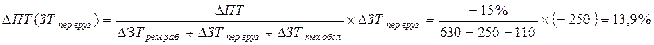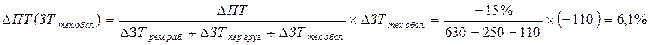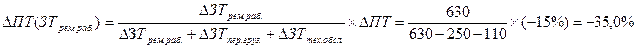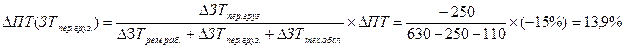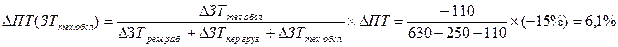Методы детерминированного факторного анализа
Вы будете перенаправлены на Автор24
Понятие детерминированного факторного анализа
Детерминированный факторный анализ – это метод исследования воздействия на объект факторов, которые связаны с результатом воздействия функционально.
То есть, детерминированный факторный анализ позволяет установить связь между итоговым показателем или функцией, а также факторами или аргументами функции. Для того, чтобы исследовать подобные зависимости необходимо соблюдать ряд требований, к которым относят:
- Рассматриваемые факторы должны относиться к реальной действительности, а не быть абстрактными. Они должны быть причиной или следствием рассматриваемого явления или объекта. Такие модели имеют высокий практический потенциал, в отличие от математических абстракций.
- Показатели рассматриваемой модели должны быть измеряемы количественно. Так же они должны иметь информационное описание.
- Рассматриваемые факторы могут быть оценены по отдельности. То есть, при исследовании взаимосвязи факторов с конечным результатом должна быть возможность увидеть их обособленное влияние на функцию. При этом их совокупное воздействие показывает прирост итогового результата.
Детерминированный анализ использует следующие виды моделей. Аддитивные модели используются в случае, если результат представляет собой совокупность нескольких факторных показателей. Математически эта зависимость отображается следующим уравнением:
$Y = x_1 + x_2 + x_3 + … x_n$
В случае, если результат воздействия факторов представляет собой их произведение, то пользуются мультипликативной моделью, которая выглядит как:
$Y = x_1 • x_2 • x_3 • … • x_n$
Если при вычислении необходимо разделить один фактор на другой, то пользуются кратными моделями, представленными такими уравнениями как:
Так же могут использоваться смешанные или комбинированные модели. Они строятся на сочетании разных комбинаций вышеперечисленных моделей. Для проведения операций с вышеперечисленными моделями могут использоваться следующие приемы. Например, прием удлинения, когда числитель формулы раскладывают на отдельные факторы. Еще один способ – способ формального разложения. В этом случае знаменатель раскладывается на составляющие факторы. Математическое уравнение:
Готовые работы на аналогичную тему
$Y = Z / X = Z / x_1 + x_2+… + x_n$
Так же применяется способ расширения, который предполагает умножение числителя и знаменателя на одну или ту же величину, что позволяет исследовать влияние фактора на функцию в целом. Метод сокращения, напротив, позволяет разделить величины на указанный фактор.
Детерминированный факторный анализ предполагает применение различных методов манипулирования действующими факторами. Как правило, он позволяет методом исключения оставлять один фактор и исследовать его влияние на функцию. Для этого специалисты могут использовать методы цепной подстановки, абсолютные и относительные разницы, индексный метод, метод долевого участия и другое.
Метод цепной подстановки
Способ цепной подстановки факторов является наиболее универсальным. Он позволяет опытным и расчетным путем оценить влияние фактора на хозяйственный результат. Сущность метода заключается в замене базисной величины фактора на фактическую. Далее осуществляется вычитание из каждой замены предыдущего значения. На примере аддитивной модели метод цепной подстановки примет вид:
- Аддитивная модель $ Y = a + b + c$. Базисный фактор $a_0$ будет последовательно заменяться на каждый фактическое значение фактора $a_1$. При этом количество замен будет равняться количеству воздействующих факторов, то есть $Y_1 = a_1 + b_1 + c_1$
- Далее из полученного значения вычитается предшествующее. Каждый фактор будет рассматриваться в двух периодах – базисном и фактическом. Баланс отклонений дельты Y составит совокупность отклонений факторов $a, b, c$.
- Полученный результат $Y_0$ и $Y_1$ покажут изменение результата под воздействием факторов в аддитивной модели, где дельта $a, b, c$ – покажет дельту изменения итога.
Метод подстановок рассчитан на оценку количественных показателей. Только рассчитав их, исследователь может обратиться к качественным показателям. Расчет значений факторов позволяет определить как каждый из них влияет на конечный результат. Однако, использование этого метода требует знаний о последовательности влияния факторов на конечный результат. Так же необходимо учитывать их взаимное подчинение, чтобы иметь возможность их систематизировать.
Метод цепных подстановок является инструментом определения влияния структурного фактора на итог. Примером может послужить расчет выручки, который зависит не только от цены реализации, но и от количества проданных товаров, их структуры. То есть, продажа товаров более высокого качества принесет большую сумму дохода, нежели от товаров более низкого качества.
Метод абсолютных разниц
Этот способ применяется для моделей, где рассматривается произведение влияния фактора на конечный результат хозяйственной деятельности. То есть, он используется для моделей аддитивного и мультпликативно-аддитивного вида. Несмотря на то, что область его применения ограничена, он активно применяется в анализе экономической работы субъектов. Оценка проводится путем умножения абсолютного значения прироста на плановое расчетное значение. Таким образом, появляется возможность рассмотреть влияние одного фактора. Значение всех остальных факторов принимается как фактическое и неизменяемое, а последующих факторов в виде базиса.
Расчет воздействия начинается с первого фактора, далее строго соблюдается последовательность влияния факторов. Рассмотрим на примере мультипликативной модели:
- $Y (a) = a • b_0 • c_0$, фактор $а$ рассматривается в динамике его изменения, остальные факторы исследуются в их базисном значении.
- $Y(b) = a_1 • b • c_0$, то есть рассматриваемый фактор $b$ берется в динамике, предыдущий фактор a оценивается по его фактическому значению, а последующий фактор c по базисному.
- $Y (c) = a_1 • b_1 • c$, здесь соблюдается тот же принцип, что и вышеуказанных моделях.
Индексный метод оценки влияния факторов оперирует относительными величинами. Он помогает получить более точное представление о воздействии факторов, так как каждый фактор в его фактическом значении делится на его базисное значение, что позволяет рассчитать индекс. С помощью индексов можно охарактеризовать исследуемое явление во времени и пространстве.
Наиболее часто в экономике используют три вида индексов, а именно, индекс Ласпейреса или индекс фактического товарооборота. Агрегатный индекс цен или индекс Паше широко применяется для оценки динамики цен и зависимости производственного выпуска. Индексы позволяют анализировать влияние факторов в том случае, если оно представлено их произведением.
Интегральный метод является наиболее точным из существующих. Он полностью убирает эффект преувеличения влияния одного фактора, и преуменьшения влияния другого. Это происходит из-за того, что факторы оказывают взаимное влияние, а значит, образуют совместный прирост итогового значения.
Все рассмотренные методы факторного анализа работают для оценки количественного влияния факторов. При этом, исследование сложных факторов подразумевает, что они будут разбиты на более простые составляющие, а затем, элементы будут проанализированы по отдельности. В этом случае, разделенные факторы будут относится ко второму уровню, который рассчитывается с помощью метода долевого участия.
Этот способ представляет собой разбивку факторов на несколько уровней. Чтобы рассчитать факторы второго порядка проводится оценка динамики их прироста. Причем анализируется их доля в общей сумме прироста. Затем осуществляется их умножение на величину влияния совокупного раскладываемого фактора.
Применение методов детерминированного факторного анализа требует соблюдения условий, позволяющих избегать элиминирования. Оно предполагает, что изменение факторов происходит не зависимо друг от друга, когда в реальности все факторы, как правило, оказывают взаимное влияние. Прирост изменения итога обычно происходит по показателю, анализируемому в последнюю очередь. При исследовании модели очень важно учитывать эту особенность, так как месторасположения фактора в цепочке воздействия может влиять на общий результат и влияние других факторов. Помимо приведенных методов, все чаще используются интегральный метод, метод логарифмический, кольцевой, экстремальный и метод взвешенных конечных разностей.
Таким образом, детерминированный факторный анализ и его методы позволяют оценивать влияние факторов на конечный результат. Он широко применяется при анализе хозяйственной деятельности отдельных субъектов хозяйствования и целых систем. Важно помнить, что ни одна структура не является закрытой, а значит, всегда подвержена воздействию других систем, событий, явлений и объектов. При этом сам предмет исследования может оказывать влияние на окружающую среду. Кроме того, детерминированный факторный анализ помогает рассматривать экономические показатели в динамике, что позволяет приблизить исследование к реальности.
Источник
Способы детерминированного факторного анализа
Детерминированный факторный анализ — это методика изучения влияния факторов на результативный показатель, связь между которыми имеет функциональный характер. То есть результативный показатель представлен в виде произведения, алгебраической суммы или частного факторов.
Этапы проведения детерминированного факторного анализа:
· построение обоснованной детерминированной факторной модели;
· выбор приема факторного анализа;
· реализация расчетных процедур;
· формулирование выводов и рекомендаций по результатам анализа.
Построение факторной модели. В детерминированной факторной модели связи между переменными жестко фиксированы и каждой конкретной величине изменения независимой переменной (фактора) соответствует строго определенное (детерминированное) изменение зависимой переменной (результативного показателя).
На этом этапе происходит моделирование взаимосвязей между результативными показателями и факторами, которые влияют на их величину. Это очень важный этап, так как если на этом этапе будет допущена ошибка, то все дальнейшие расчеты не дадут верных результатов. Смысл этапа состоит в том, чтобы в форме математического уравнения выразить взаимосвязь исследуемого показателя и факторов.
Существует правило, которое заключается в следующем: любое расширение детерминированной факторной модели не должно противоречить логике связи «причина — следствие». То есть факторы, которые входят в модель, должны находиться в причинно-следственной связи с показателем. Кроме того, все показатели факторной модели должны быть количественно измеряемыми.
В зависимости от числа факторов, используемых в модели, модель может быть двух-, трех-, четырехфакторной и т. д.
Выделяют следующие виды детерминированных факторных моделей:
— аддитивная модель. Это модель, в которую факторы входят в виде алгебраической суммы

— мультипликативная модель. Это модель, в которую факторы входят в виде произведения

— кратная модель. Это модель, представляющая собой отношение факторов, то есть результативный показатель получают делением одного фактора на величину другого
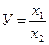
— смешанная модель. Это модели, которые сочетают в себе различные комбинации предыдущих моделей

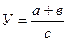

Следующим этапом проведения детерминированного факторного анализа является выбор приема факторного анализа. Существует несколько способов проведения детерминированного факторного анализа:
1. Способ цепных подстановок.Способ цепных подстановок позволяет измерить влияние каждого отдельного фактора на прирост результативного показателя. Суть способа цепных подстановок заключается в последовательной замене базисной величины каждого фактора отчетными значениями и в оценке влияния произведенной замены на результативный показатель. К достоинству этого метода относится достаточная простота и универсальность. Способ цепных подстановок можно использовать для всех видов детерминированных факторных моделей (аддитивных, мультипликативных, кратных, комбинированных).
При использовании этого способа большое значение имеет очередность расстановки факторов в факторной модели и, соответственно, последовательность изменения значений факторов, так как от этого зависит количественная оценка влияния каждого фактора.
Для метода цепных подстановок должна применяться правильно построенная детерминированная факторная модель, должна соблюдаться определенная очередность в расстановке факторов. Если в факторной модели присутствуют количественные и качественные факторы, то замену факторов следует начинать с количественного фактора.
Количественные факторы отражают количественную определенность явлений. Количественные факторы могут выражаться как в стоимостном, так и в натуральном измерителях. Например, количественные факторы характеризуют объем производства и реализации продукции, причем величина этих факторов может быть выражена как в рублях, так и в штуках, метрах и т. д.
Качественные факторы характеризуют внутренние свойства, особенности и признаки изучаемых объектов. Например, качественным фактором является жирность молока, производительность труда, качество продукции и т. д.
Алгоритм расчета способом цепной подстановки для двухфакторной мультипликативной модели выглядит следующим образом:
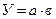
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:


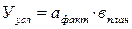
Далее определяют общее изменение результата (У):

Определяют влияние факторов:
— количественного фактора по формуле

— качественного фактора по формуле

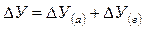
Рассмотрим алгоритм расчета на конкретном примере.
Пример 1.По исходным данным таблицы 1 определите отклонение объема производства в целом и за счет влияния факторов.
Таблица 1 – Исходные данные для факторного анализа
| Показатель | Плановое значение | Фактическое значение |
| Среднегодовая численность рабочих, чел. | ||
| Среднегодовая выработка одного работника, тыс.р. |
Решение
Составляется двухфакторная мультипликативная модель, где численность рабочих — это количественный фактор, и поэтому в модели он идет первым, а выработка — качественный фактор, и он находится за количественным.
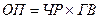
Рассчитываются плановое, фактическое и условное значения объема производства:
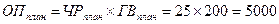
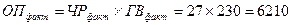
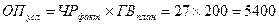
Далее определяется общее отклонение объема производства:
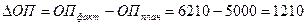
Вывод: За анализируемый период объем производства увеличился на 1210 тыс.р.
Определяется влияние численности работников и среднегодовой выработки на объем производства:
— влияние численности работников определяется по формуле:
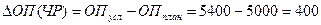
Вывод: При увеличении численности работников объем производства возрастет на 400 тыс.р.
— влияние среднегодовой выработки определяется по формуле:
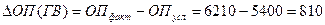
Вывод: Увеличение среднегодовой выработки одного рабочего привело к повышению объема производства на 810 тыс.р.
Проверка:
2. Способ абсолютных разниц.Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и мультипликативно-аддитивных моделях. Его использование ограничено, но, благодаря своей простоте, он получил широкое применение в экономическом анализе. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.
При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Рассмотрим алгоритм расчета длямультипликативной факторной модели типа:

где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:
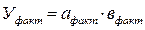

Далее определяют общее изменение результата (У):
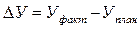
Определяют влияние факторов:
— количественного фактора по формуле
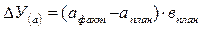
— качественного фактора по формуле
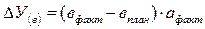
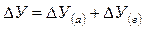
Как видно из приведенной схемы, расчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.
Рассмотрим методику расчета влияния факторов этим способом для четырехфакторной мультипликативной модели валовой продукции.
Пример 2.По исходным данным таблицы 2 определите отклонение валовой продукции в целом и за счет влияния факторов.
Таблица 2 – Исходные данные для факторного анализа
| Показатель | Плановое значение | Фактическое значение |
| Среднегодовая численность рабочих, чел. | ||
| Количество дней, отработанных одним рабочим за год, дн | ||
| Средняя продолжительность рабочего дня, ч | 8,0 | 7,6 |
| Среднечасовая выработка, тыс.р. |
Решение:
Составляется четырехфакторная мультипликативная модель:
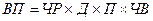
Сначала рассчитываются плановое и фактическое значение выпуска продукции:
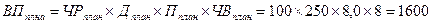
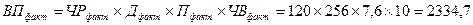
Далее определяется общее отклонение выпуска продукции:
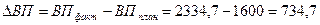
Вывод: За анализируемый период выпуск продукции увеличился на 734,7 млн.р.
Определяется влияние каждого фактора исходной модели на изменение выпуска продукции:
— влияние численности рабочих на выпуск продукции рассчитывается по формуле
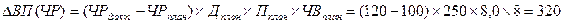
Вывод: При увеличении численности работников выпуск продукции возрастет на 320 млн.р.
— влияние количества дней, отработанных одним рабочим за год, на выпуск продукции определяется по формуле

Вывод: Увеличение числа дней, отработанных одним работником за год, привело к повышению выпуска продукции на 46,1 млн.р.
— влияние средней продолжительности рабочего дня на выпуск продукции определяется по формуле:
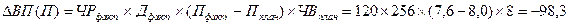
Вывод: Сокращение продолжительности рабочего дня привело к снижению выпуска продукции на 98,3 млн.р.
— влияние среднечасовой выработки на выпуск продукции определяется по формуле:
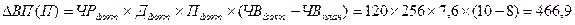
Вывод: При увеличении среднечасовой выработки выпуск продукции возрастет на 466,9 млн.р.
Проверка:
3. Способ относительных разниц.Применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных и аддитивно-мультипликативных моделях типа. Он значительно проще цепных подстановок, что при определенных обстоятельствах делает его очень эффективным. Это, прежде всего, касается тех случаев, когда исходные данные содержат уже определенные ранее относительные приросты факторных показателей в процентах или коэффициентах.
Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа:
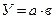
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:
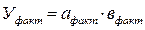
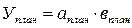
Далее определяют общее изменение результата (У):
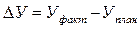
Определяют влияние факторов:
— количественного фактора по формуле
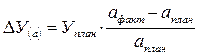
— качественного фактора по формуле
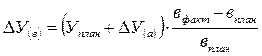
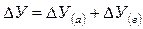
Пример 3.Закрепим рассмотренную методику на основе данных таблицы 2.
Решение.
Как и в способе абсолютных разниц, сначала определяют плановые и фактические показатели выпуска продукции:
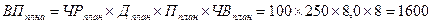
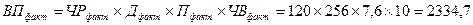
Далее определяется общее отклонение выпуска продукции:

Вывод: За анализируемый период выпуск продукции увеличился на 734,7 млн.р.
Определяется влияние каждого фактора исходной модели на изменение выпуска продукции:
— влияние численности рабочих на выпуск продукции рассчитывается по формуле
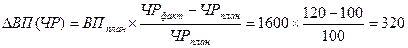
Вывод: При увеличении численности работников выпуск продукции возрастет на 320 млн.р.
— влияние количества дней, отработанных одним рабочим за год, на выпуск продукции определяется по формуле
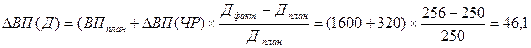
Вывод: Увеличение числа дней отработанных одним работником за год привело к повышению выпуска продукции на 46,1 млн.р.
— влияние средней продолжительности рабочего дня на выпуск продукции определяется по формуле
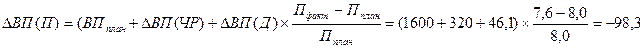
Вывод: Сокращение продолжительности рабочего дня привело к снижению выпуска продукции на 98,3 млн.р.
— влияние среднечасовой выработки на выпуск продукции определяется по формуле
Вывод: При увеличении среднечасовой выработки выпуск продукции возрастет на 466,9 млн.р.
Проверка:
4. Индексный метод.Основан на относительных показателях динамики, пространственных сравнений. Индекс показывает процентное или долевое изменение определенного значения за какой-то период времени.
Применяется этот метод только в кратных и мультипликативных, двухфакторных моделях. С помощью индексов решаются следующие задачи:
· индексы позволяют измерять изменение (динамику) сложных явлений;
· с помощью индексов можно определить влияние различных факторов на изменение уровня результативного показателя;
· индексы являются показателями сравнений не только с прошлым периодом (сравнений во времени), но с другой территорией (сравнение в пространстве), а также с нормативами, планами, прогнозами. Для факторного анализа больше подходят агрегатные индексы.
Рассмотрим методику данного метода на примере двухфакторной мультипликативной модели:
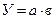
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:

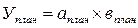
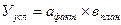
Далее определяют общее изменение результата (У):
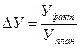
Определяют влияние факторов:
— количественного фактора по формуле
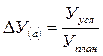
— качественного фактора по формуле
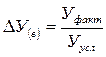
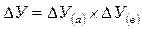
Пример 4.По данным таблицы 1 рассчитаем отклонение объема производства в целом и за счет влияния факторов.
Решение.
Составляется двухфакторная мультипликативная модель.
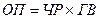
Рассчитываются плановое, фактическое и условное значения объема производства:
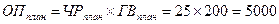

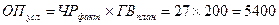
Далее определяется общее отклонение объема производства:
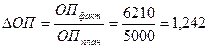
Вывод: За анализируемый период объем производства увеличился на 24,2 %.
Определяется влияние численности работников и среднегодовой выработки на объем производства:
— влияние численности работников определяется по формуле
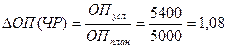
Вывод: При увеличении численности работников объем производства возрастет на 8 %.
— влияние среднегодовой выработки определяется по формуле:
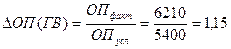
Вывод: Увеличение среднегодовой выработки одного рабочего привело к повышению объема производства на 15 %.
Проверка:
5. Интегральный метод.При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом же деле они изменяются совместно, взаимосвязанно и от этого взаимодействия получается дополнительный прирост результативного показателя, который при применении способов элиминирования присоединяется к одному из факторов, как правило, к последнему. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели.
Рассмотрим методику интегрального метода для двухфакторной модели:
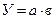
где а – количественный фактор;
в – качественный фактор.
Анализ начинают с того, что рассчитывают:
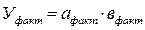
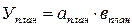
Далее определяют общее изменение результата (У):
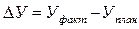
Определяют влияние факторов:
— количественного фактора по формуле

— качественного фактора по формуле

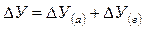
Пример 5.По данным таблицы 1 определить отклонение объема производства в целом и за счет влияния факторов.
Решение:
Составляется двухфакторная мультипликативная модель.
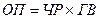
Рассчитываются плановое и фактическое значения объема производства:
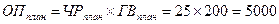

Далее определяют общее изменение результата:

Вывод: За анализируемый период объем производства увеличился на 1210 тыс.р.
Определяют влияние факторов:
— влияние численности работников на изменение объема производства определяется по формуле
Вывод: При увеличении числа работников объем производства возрастет на 430 тыс.р.
— влияние среднегодовой выработки одним работником на изменение объема производства определяется по формуле
Вывод: Увеличение среднегодовой выработки привело к повышению объема производства на 780 тыс.р.
Проверка: 430+780=12010 тыс.р.
6. Способ пропорционального деления (долевого участия).
Способ пропорционального деления относится к способам детерминированного анализа и используется для расчета влияния факторов в детерминированных аддитивных, кратно-аддитивных и мультипликативных моделях. Наиболее эффективен этот способ для определения факторов 2го, 3го и более высокого порядка.
Способ долевого участия– это модификация способа цепных подстановок. Этот метод используется для аддитивных и кратных моделей.
Сначала определяется влияние факторов 1-го порядка любым из ранее приведенных методов, а затем находится влияние факторов 2-го порядка.
Способ пропорционального деления
— влияние фактора с рассчитывается по формуле
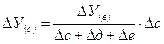
— влияние фактора д:
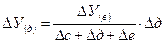
— влияние фактора е:

Способ долевого участия.
— влияние фактора с по формуле

— влияние фактора д:
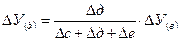
— влияние фактора е:

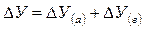
Пример 6.Производительность труда (ПТ) в текущем периоде по сравнению с прошлым снизилась на 15% из-за увеличения затрат рабочего времени (ЗРВ) на 270 чел.-ч.
При этом затраты труда на ремонтных работах (ЗТрем.раб.) увеличились на 630 чел.-ч, и снизились на перевозке грузов (ЗТпер.груз.) на 250 чел.-ч, на техническом обслуживании (ЗТтех.обсл.) — на 110 чел.-ч. Определить влияние факторов на изменение производительности труда методом пропорционального деления и долевого участия.
Решение.
Метод пропорционального деления
1. Расчет изменения производительности труда (ПТ) под влиянием изменения затрат труда на ремонтных работах (ЗТрем.раб.):
2. Изменение уровня производительности труда (ПТ) через изменение затрат на перевозки грузов (ЗТпер.груз.):
3. Динамика производительности труда ПТ в результате изменения затрат труда на техническое обслуживание ЗТтех.обсл.:
Следовательно, производительность труда в отчетном периоде снизилась по сравнению с предыдущим периодом на 15%. Увеличение затрат рабочего времени на ремонтных работах привело к снижению уровня производительности труда на 35%, а сокращение затрат времени на перевозку грузов и техническое обслуживание способствовало росту производительности труда на 13,9 и 6,1% соответственно.
Метод долевого участия
1. Влияние изменения затрат труда на ремонтных работах на производительность труда рассчитывается по формуле
2. Изменение уровня производительности труда под влиянием изменения затрат на перевозку грузов:
3. Динамика производительности труда в результате изменения затрат труда на техническое обслуживание:
Как видно из расчетов, при применении метода долевого участия получились аналогичные результаты, как и при методе пропорционального деления.
Источник