Способа вращения при решений метрических задач

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник

Основные задачи, решаемые способом вращения

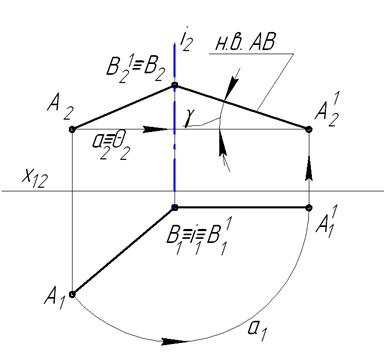
Задача№1. Преобразовать прямую общего положения во фронтальную прямую уровня (рисунок 1.4.14).

Рассмотрим решение задачи, вращая прямую АВ вокруг горизонтально-проецирующей прямой i₁. Чтобы прямая АВ преобразовалась во фронтальную прямую уровня, необходимо ее повернуть вокруг оси, пока она не примет положение, параллельное фронтальной плоскости проекций. Если заданный отрезок прямой требуется повернуть до положения, параллельного плоскости П₁, то ось вращения следует расположить перпендикулярно П₂, если прямую следует повернуть до положения параллельного П₂, то ось вращения должна быть расположена перпендикулярно к плоскости П₁. Для упрощения графического решения этой задачи горизонтально проецирующую ось вращения i выберем проходящей через точку В. Тогда, при вращении прямой вокруг оси, точка В останется неподвижной (В₁≡В₁ 1 , В₂≡В₂ 1 ), а точка А₁ примет положение А₁ 1 и А₂ 1 . Траектория точки А является часть окружности а, лежащей в плоскости θ, параллельной П₁. Поэтому а₂≡θ₂, а₁ – окружность с центром в i₁, радиус которой равен отрезку А₁В₁. Преобразованная прямая будет являться фронтальной прямой уровня, а отрезок А₂В₂ – его натуральной величиной. Также в задаче определяется натуральная величина угла наклона φ прямой АВ к горизонтальной плоскости проекций.

Рисунок 1.4.14 – Решение первой основной задачи способом вращения

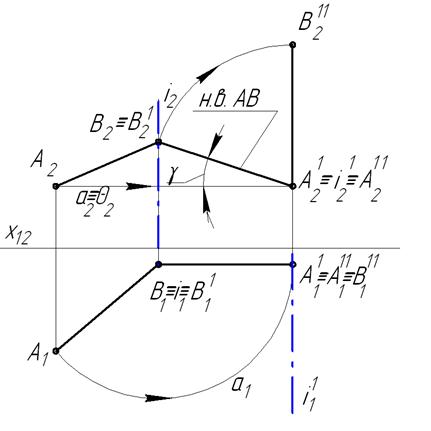
Задача №2. Преобразовать прямую общего положения в горизонтально проецирующую прямую (Рисунок 1.4.15).

Эта задача решается при помощи двух преобразований: сначала прямую АВ преобразуем в прямую уровня (смотри задачу №1), а затем , чтобы прямая была перпендикулярно горизонтальной плоскости проекций, введем новую ось вращения i 1 , перпендикулярную фронтальной плоскости проекций и проходящую через точку А. В этом случае точка А останется неподвижной, а точка В на чертеже примет положение В₂ 11 . Траектория точки В является часть окружности, лежащей в плоскости, параллельной фронтальной плоскости проекций, поэтому в горизонтальной плоскости проекций она совпадет с горизонтальной проекцией преобразованной прямой АВ (А₁ 1 В₁ 1 ). Горизонтальная проекция прямой, после второго преобразования, будет являться точкой А₁ 11 В₁ 11 , т.е. прямая станет горизонтально проецирующей прямой.

Рисунок 1.4.15 — Решение второй основной задачи способом вращения

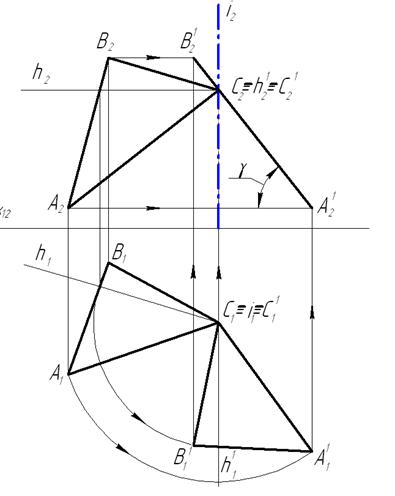
Задача №3. Преобразовать плоскость общего положения во фронтально проецирующую (рисунок 1.4.16). Плоскость задана ΔABC.

Предварительно в плоскости проводим прямую уровня, в нашем случае – это горизонталь h. Заметим, если плоскость преобразуется в горизонтально проецирующую, то это – фронталь f. Через вершину В треугольника проведем горизонтально проецирующую ось вращения i и вокруг нее будем вращать треугольник до положения, перпендикулярного плоскости П₁. Для этого на чертеже поворачиваем фронтальную проекцию горизонтали h₁ вокруг горизонтальной проекцией оси вращения i₁ так, чтобы она по отношению к оси х располагалась перпендикулярно. При этом форма повернутой горизонтальной проекции треугольника A₁ 1 B₁ 1 C₁ 1 осталась неизменной по отношению к проекции A₁B₁C₁. Так как горизонталь повернулась перпендикулярно фронтальной плоскости проекций, то на эту плоскость она проецируется в точку, а сам треугольник – в виде отрезка прямой A₂ 1 B₂ 1 C₂ 1 . Плоскость треугольника стала фронтально-проецирующей, а угол γ между фронтальной его проекцией и оси х – натуральной величиной угла наклона плоскости ΔABC к горизонтальной плоскости проекций.

Рисунок 1.4.16 — Решение третьей основной задачи способом вращения

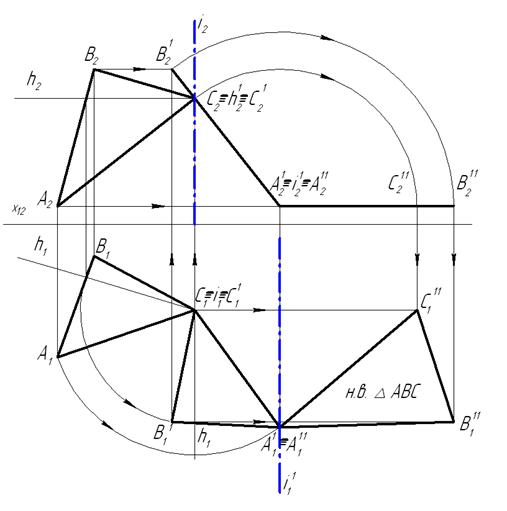
Задача №4. Преобразовать плоскость общего положения в горизонтальную плоскость уровня (рисунок 1.4.17).

Для решения этой задачи необходимо выполнить два преобразования (вращения): сначала повернуть плоскость, чтобы она стала фронтально проецирующей (смотри задачу №3), а затем, повернув вторично плоскость так, чтобы плоскость располагалась по отношению к горизонтальной плоскости проекций параллельно. Для второго вращения введем еще одну фронтально проецирующую ось вращения i 1 , проходящую через точку А. На чертеже строим новую фронтальную проекцию ΔABC(A₂ 11 B₂ 11 C₂ 11 ), повернутую вокруг i₂ 1 до горизонтального положения. В горизонтальной проекции, в точках пересечения линий связи проекций одноименных точек треугольника, получим положение треугольника в горизонтальной плоскости уровня, а следовательно натуральную величину самого треугольника ABC.

Рисунок 1.4.17 — Решение четвертой основной задачи способом вращения

Источник

8. Метрические задачи и способы их решения

Метрическими принято считать задачи, в условии или в решении которых присутствует численная характеристика. К метрическим задачам относятся задачи на построение изображений фигур по их размерам или координатам из точек, измерение расстояний, углов, площадей и другие. Метрические задачи бывают комплексными и включают в своем составе позиционные задачи. Из всего многообразия метрических задач выделяют две задачи, которые называются основными метрическими задачами.

Первая задача — задача на перпендикулярность прямой линии и плоскости (п.7.1).

Вторая основная задача — задача на измерение расстояния между двумя точками способом прямоугольного треугольника.

Эти задачи называют основными потому, что на их основании можно решить любую другую метрическую задачу, то есть решение любой метрической задачи можно свести к решению основных метрических задач.

Кроме этого, метрические задачи можно решать и способами преобразования комплексного чертежа.

8.1. Решение метрических задач в общем виде

Рассмотрим решение одной из метрических задач на примере, когда ее решение сводится к решению двух основных метрических задач.

Пример (рис.8.1).Измерить расстояние от точки А до плоскости (hf).

1.Опустим из точки А перпендикуляр на плоскость (hf) и найдем его основание — точку К.

2.Способом прямоугольного треугольника измерим истинную величину отрезка АК.

8.2. Решение метрических задач способами преобразования комплексного чертежа

Способами преобразования комплексного чертежа могут быть решены только те метрические задачи, которые имеют только один геометрический элемент, несущий на себе одну искомую численную характеристику.

Алгоритм решения метрической задачи с помощью преобразования комплексного чертежа сводится к следующему:

1) определяется геометрический элемент оригинала, несущий на себе искомую численную характеристику и,

2) определяется “решающее положение” оригинала по отношению к плоскости проекций. (Решающим положением оригинала называют такое положение, при котором геометрический элемент, несущий на себе искомую численную характеристику, может быть спроецирован на плоскость проекций без искажений).

Решающих положений может быть только четыре, и им соответствуют и четыре известных задачи на преобразование комплексного чертежа.

8.3. Измерение расстояний

1.Расстояние от точки до прямой измеряется длиной перпендикуляра, опущенного из точки на данную прямую. Это расстояние будет проецироваться на плоскость проекций без искажения в двух случаях:

когда прямая перпендикулярна плоскости проекций, то есть когда решена вторая задача на преобразование (рис.8.2);

когда прямая и точка расположены в плоскости, параллельной плоскости проекций, то есть когда решена четвертая основная задача (рис.8.3).

2.Расстояние между двумя скрещивающимися прямыми будет проецироваться на плоскость чертежа без искажения, когда одна из прямых займет положение, перпендикулярное к одной из плоскостей проекций, то есть когда будет решена вторая основная задача на преобразование (рис.8.4).

3.Расстояние между двумя параллельными прямыми будет проецироваться на плоскость проекций в истинную величину в двух случаях:

когда прямые расположатся перпендикулярно плоскости проекций;

будут лежать в плоскости, параллельной плоскости проекций, то есть когда будут решены соответственно вторая и четвертая основные задачи (рис.8.5 и 8.6).

4.Расстояние от точки до плоскости проецируется на плоскость проекций без искажения, когда заданная плоскость будет проецирующей по отношению к плоскости проекций, то есть будет решена третья основная задача на преобразование чертежа (рис.8.7).

Источник