Способ заполнения пропущенных значений
К сожалению, на практике в ходе сбора данных далеко не всегда удается полностью укомплектовать исходные таблицы. Пропуски отдельных значений являются повсеместным явлением и поэтому, прежде чем начать применять статистические методы, обрабатываемые данные следует привести к “каноническому” виду. Для этого необходимо либо удалить фрагменты объектов с недостающими элементами, либо заменить имеющиеся пропуски на некоторые разумные значения.
Проблема “борьбы с пропусками” столь же сложна, как и сама статистика, поскольку в этой области существует впечатляющее множество подходов. В русскоязычных книгах по использованию R (Кабаков, 2014; Мастицкий, Шитиков, 2015) бегло представлены только некоторые функции пакета mice, который, несмотря на свою “продвинутость”, мало удобен для практической работы с данными умеренного и большого объема. Хорошей альтернативой являются методы «knnImpute» , «bagImpute» и «medianImpute» функции preProcess() из пакета caret , которую мы рассмотрели в разделе 3.3 как инструмент для трансформации данных.
Используем в качестве примера для дальнейших упражнений таблицу algae , включенную в пакет DMwR и содержащую данные гидробиологических исследований обилия водорослей в различных реках. Каждое из 200 наблюдений содержит информацию о 18 переменных, в том числе:
- три номинальных переменных, описывающих размеры size = c(«large», «medium», «small») и скорость течения реки speed = c(«high», «low», «medium») , а также время года season = c(«autumn», «spring», «summer», «winter») , сопряженное с моментом взятия проб;
- 8 переменных, составляющих комплекс наблюдаемых гидрохимических показателей: максимальное значение рН mxPH (1), минимальное содержание кислорода mnO2 (2), хлориды Cl (10), нитраты NO3 (2), ионы аммония NH4 (2), орто-фосфаты oPO4 (2), общий минеральный фосфор PO4 (2) и количество хлорофилла а Chla (12) (в скобках приведено число пропущенных значений);
- средняя численность каждой из 7 групп водорослей a1 — a7 (видовой состав не идентифицировался).
Читатель может самостоятельно воспользоваться функциями описательной статистики summary() или describe() из пакета Hmisc , а мы постараемся поддержать добрую традицию и привести парочку примеров диаграмм, построенных с использованием пакета ggplot2 (рис. 3.4):
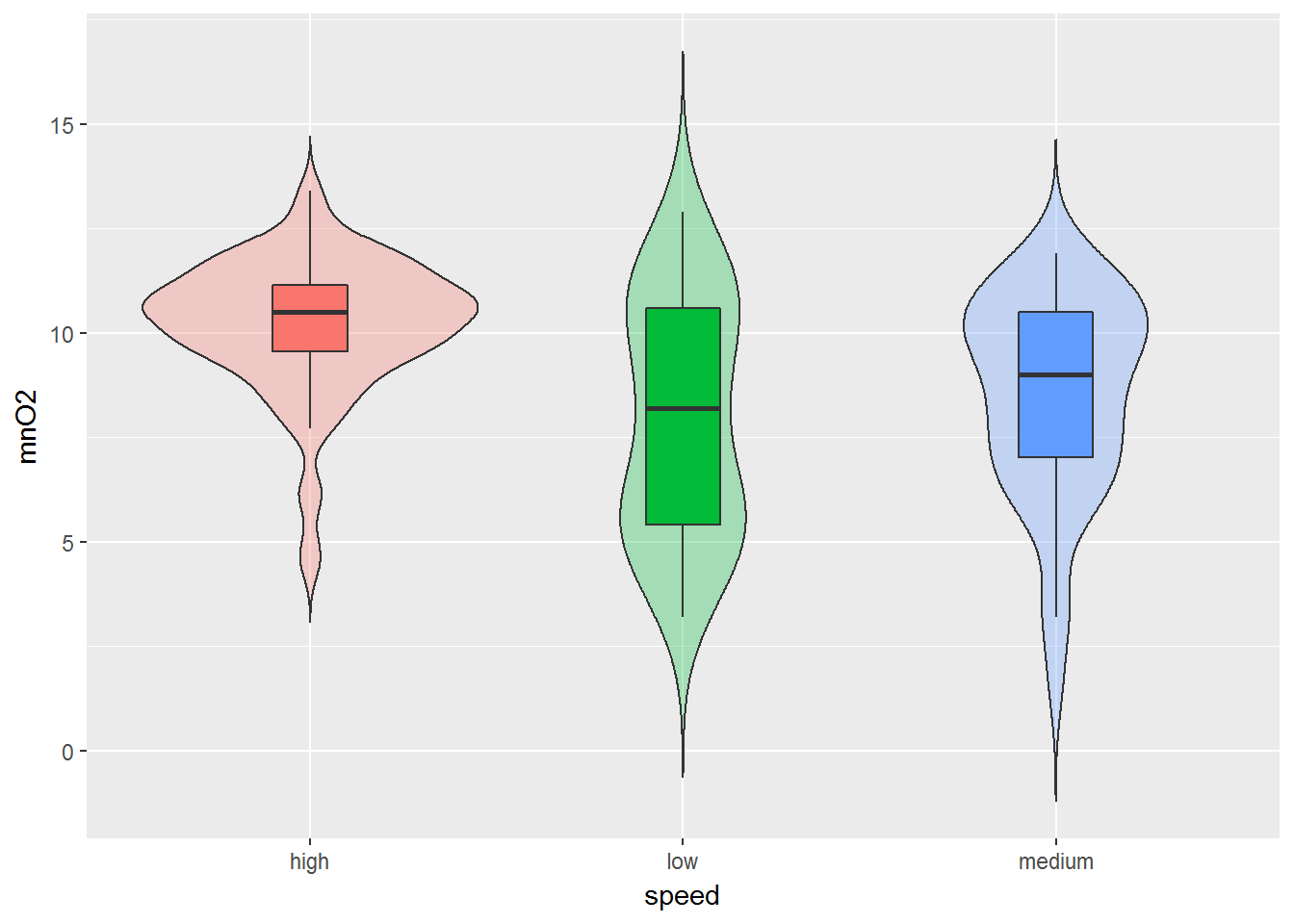
Рисунок 3.4: Распределения значений содержания кислорода в воде рек с разной скоростью течения
На рис. 3.4 мы получили так называемую “скрипичную диаграмму” (violin plot), которая объединяет в себе идеи диаграмм размахов и кривых распределения вероятности. Суть достаточно проста: продольные края “ящиков с усами” (для сравнения приведены тоже) замещаются кривыми плотности вероятности. В итоге, например, легко можно выяснить не только тот факт, что в потоках с быстрым течением (high) содержание кислорода выше, но и ознакомиться с характером распределения соответствующих значений.
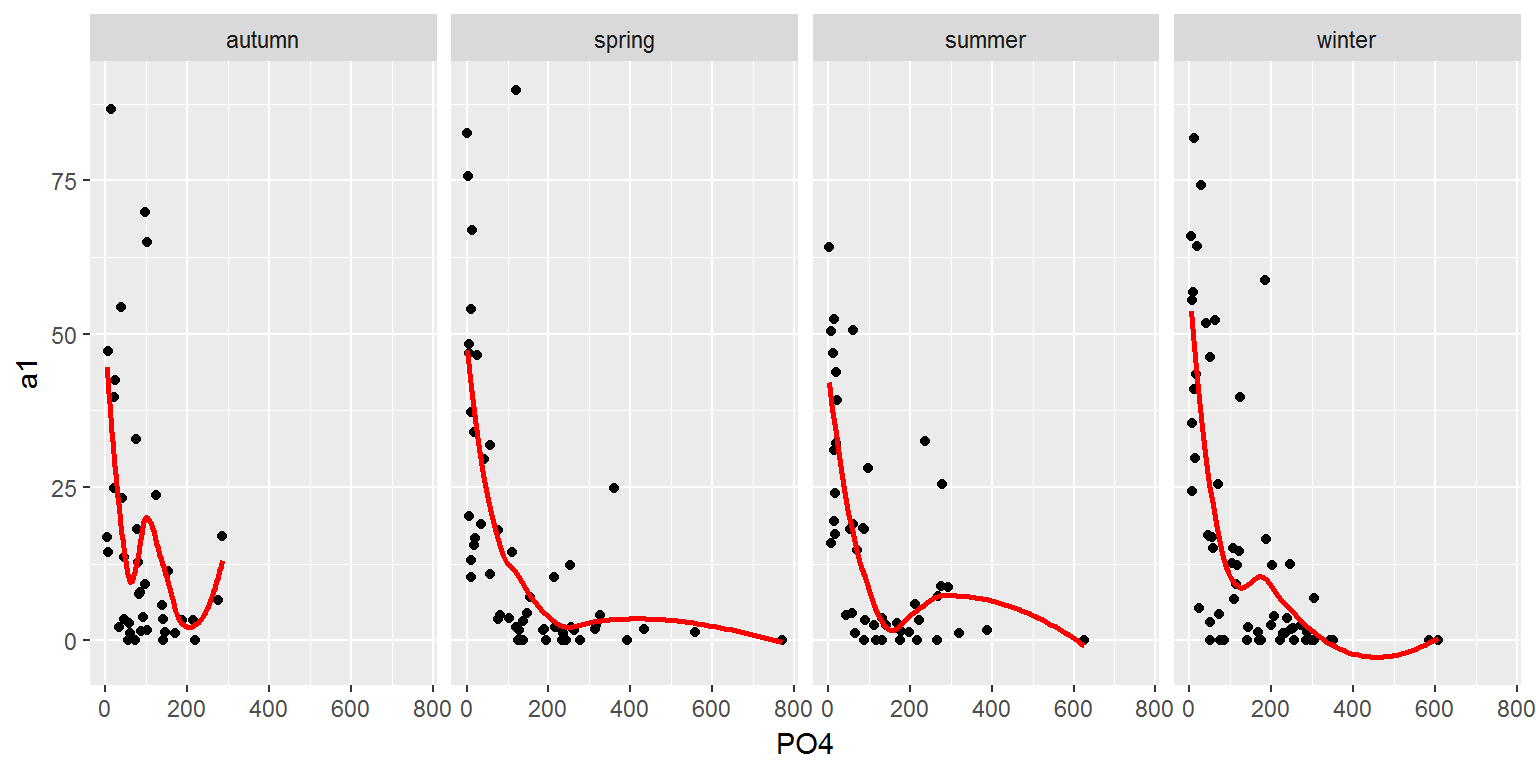
Другой пример — категоризованные графики, удобные для визуализации данных, разбитых на отдельные подмножества (категории), каждое из которых отображается в отдельной диаграмме подходящего типа. Такие диаграммы, или “панели” (от англ. panels, facets или multiples), определенным образом упорядочиваются и размещаются на одной странице. Из графиков, представленных на рис. 3.5, легко увидеть, что численность водорослей группы а1 падает с увеличением концентрации фосфатов.
Рисунок 3.5: Графики изменения обилия водорослей в зависимости от содержания минерального фосфора в разное время года
Однако в контексте темы этого раздела важно обратить внимание на то, что мы все время старались блокировать появление пропущенных значений: algae[!is.na(algae$PO4), ] . Если в обрабатываемой таблице обнаружены недостающие данные, то в общих чертах можно избрать одну из следующих возможных стратегий:
- удалить строки с неопределенностями;
- заполнить неизвестные значения выборочными статистиками соответствующей переменной (среднее, медиана и т.д.), полагая, что взаимосвязь между переменными в имеющемся наборе данных отсутствует (это соответствует известному “наивному” подходу);
- заполнить неизвестные значения с учетом корреляции между переменными или меры близости между наблюдениями; постараться обходить эту неприятную ситуацию, используя, например, формальный параметр na.rm некоторых функций.
Последняя альтернатива является наиболее ограничивающей, поскольку она далеко не во всех случаях позволяет осуществить необходимый анализ. В свою очередь, удаление целых строк данных слишком радикально и может привести к серьезным потерям важной информации:
Можно удалить не все строки, а только те, в которых число пропущенных значений превышает, например, 20% от общего числа переменных, для чего существует специальная функция из пакета DMwR :
В результате мы удалили только две строки (62-ю и 199-ю), где число пропущенных значений больше одного. Обратите внимание, что выполняя команду data(algae) , мы каждый раз обновляем в памяти содержимое этого набора данных.
Если мы готовы принять гипотезу о том, что зависимостей между переменными нет, то простым и часто весьма эффективным способом заполнения пропусков является использование средних значений. В том случае, если есть сомнения в нормальности распределения данных, предпочтительнее использовать медиану. Покажем, как это можно сделать с использованием функции preProcess() из пакета caret :
Альтернативой “наивному” подходу является учет структуры связей между переменными. Например, можно воспользоваться тем, что между двумя формами фосфора oPO4 и PO4 существует тесная корреляционная связь. Тогда, например, можно избавиться от некоторых неопределенностей в показателе PO4 , вычислив его пропущенные значения по уравнению простой регрессии:
Одно из пропущенных значений удалось восстановить.
Разумеется, легко придти к мысли не утруждать себя перебором всех возможных корреляций, а учесть все связи одновременно и целиком. Использование метода «bagImpute» осуществляет для каждой из имеющихся переменных построение множественной бутстреп-агрегированной модели, или бэггинг-модели (bagging), на основе деревьев регрессии, используя все остальные переменные в качестве предикторов. Этот метод мудр и точен, но требует значительных затрат времени на вычисление, особенно при работе с данными большого объема:
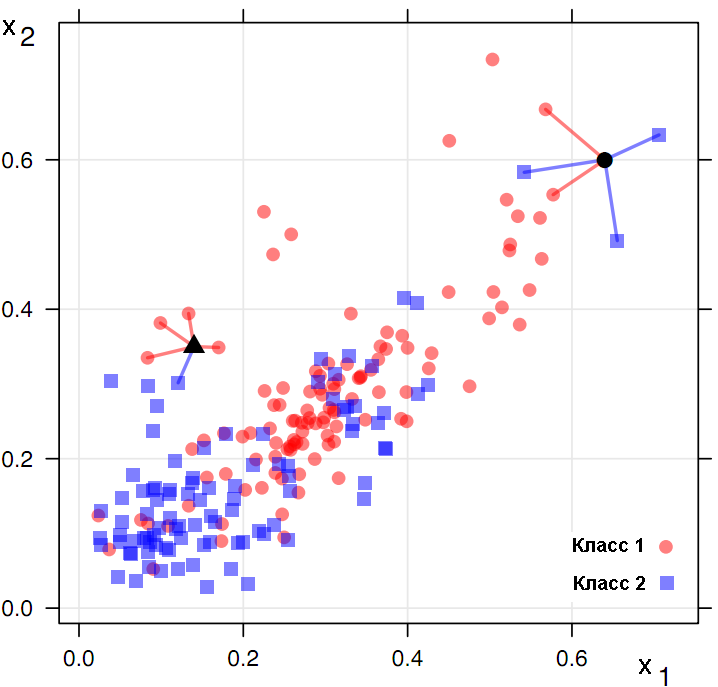
Наконец, третий метод функции preProcess() для заполнения пропусков — «knnImpute» — основан на простейшем, но чрезвычайно эффективном алгоритме k ближайших соседей (k-nearest neighbours) или kNN. В основе метода kNN лежит гипотеза о том, что тестируемый объект d будет иметь примерно тот же набор признаков, что и обучающие объекты в локальной области его ближайшего окружения (рис. 3.6).
Рисунок 3.6: Интерпретация метода k ближайших соседей
Если речь идет о классификации, то неизвестный класс объекта определяется голосованием \(k\) его ближайших соседей (на рис. 3.6 \(k = 5\) ). kNN-регрессия оценивает значение неизвестной координаты \(Y\) , усредняя известные ее величины для тех же \(k\) соседних точек.
Одна из важных проблем kNN — выбор метрики, на основе которой оценивается близость объектов. Наиболее общей формулой для подсчета расстояния в m-мерном пространстве между объектами \(\mathbf
где \(i\) изменяется от 1 до \(m\) , а \(r\) и \(p\) — задаваемые исследователем параметры, с помощью которых можно осуществить нелинейное масштабирование расстояний между объектами. Мера расстояния по Евклиду получается, если принять в метрике Минковского \(r = p = 2\) , и является, по-видимому, наиболее общей мерой расстояния, знакомой всем со школы по теореме Пифагора. При \(r = p = 1\) имеем “манхеттенское расстояние” (или “расстояние городских кварталов”), не столь контрастно оценивающее большие разности координат \(x\) . Вторая проблема метода kNN заключается в решении вопроса о том, на мнение какого числа соседей \(k\) нам целесообразно положиться? В свое время мы обсудим этот вопрос детально, а сейчас будем ориентироваться на значение \(k = 5\) , используемое по умолчанию:
Получив в результате применения predict() матрицу переменных с пропущенными значениями, заполненными этим методом, мы с удивлением обнаруживаем, что данные оказались стандартизованными (т.е. центрированными и нормированными на стандартное отклонение). Но а как иначе можно было вычислить меру близости по переменным, измеренным в разных шкалах? Пришлось для возвращения в исходное состояние применить обратную операцию:
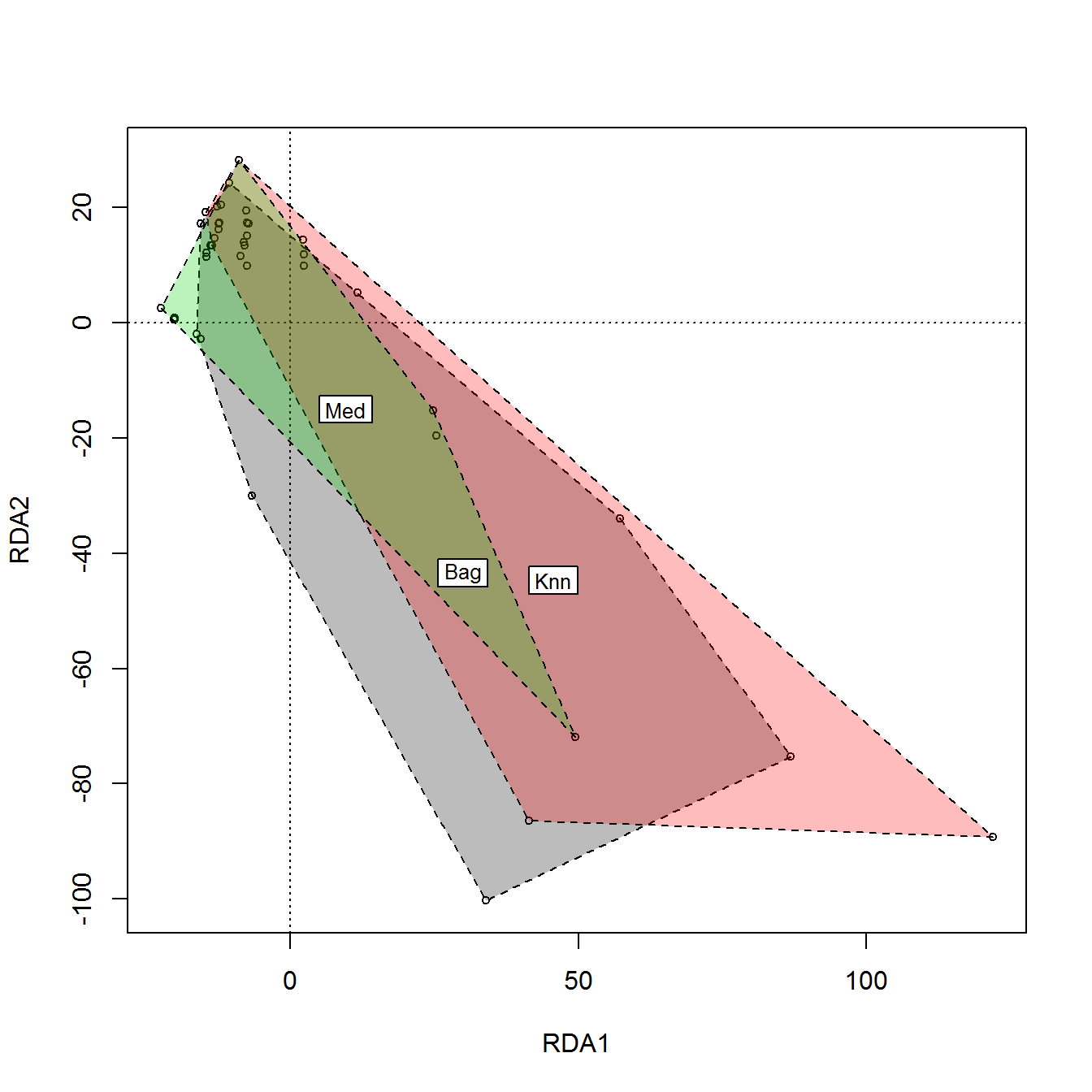
Наконец, зададимся следующим закономерным вопросом: а какой метод лучше? Обычно эта проблема не имеет теоретического решения, и исследователь полагается на собственную интуицию и опыт. Но мы можем оценить, насколько расходятся между собой результаты, полученные каждым способом заполнения. Для этого сформируем блок данных из \(3 \times 16 = 48\) строк исходной таблицы с пропусками, заполненными тремя методами ( «Med» , «Bag» , «Knn» ), и выполним снижение размерности пространства переменных методом главных компонент в двумерное (см. раздел 2.4). Посмотрим, как “лягут карты” на плоскости (рис. 3.7):
Рисунок 3.7: Ординационная диаграмма блоков данных таблицы algae с пропущенными значениями, заполненными разными способами
На рис. 3.7 мы выделили контуром (hull), проведенным через крайние точки, области каждого из трех блоков данных и поместили метку метода в центры тяжести полученных многоугольников. Понятно, что медианное заполнение характеризуется меньшей вариацией результатов, поскольку игнорирует специфичность свойств каждого объекта. Оба других метода, учитывающих внутреннюю структуру данных, дали приблизительно похожие результаты.
Источник
R: обработка пропущенных значений
Набор данных и подготовка
Будем использовать набор данных BostonHousing из пакета mlbench для иллюстрации разных подходов к обработке пропущенных значений. Хотя в исходных данных BostonHousing нет пропущенных значений, я внесу их случайным образом. Благодаря этому мы сможем сравнивать вычисленные пропущенные значения с фактическими, чтобы оценить эффективность подходов к восстановлению данных. Давайте начнем с импорта данных из пакета mlbench и случайным образом внесем пропущенные значения (NA).
Были внесены пропущенные значения. И хотя мы знаем, где они, давайте сделаем небольшую проверку с помощью mice::md.pattern .
В принципе, есть четыре способа обработки пропущенных значений.
1. Удаление данных
Если в вашем наборе сравнительно большое количество данных, где все требуемые классы достаточно представлены в данных режима обучения, то попробуйте удалить данные (строки), содержащие пропущенные значения (или не учитывать пропущенные значения при создании модели, например, установив na.action=na.omit ). Убедитесь, что после удаления данных у вас:
- достаточно точек, чтобы модель не потеряла достоверность;
- не появилась погрешность (т.е. непропорциональность или отсутствие какого-либо класса).
2. Удаление переменной
Если в какой-то конкретной переменной больше пропущенных значений, чем в остальных вместе взятых, и если удалив ее, тем самым можно сохранить много данных, я бы предложил удалить эту переменную. Конечно, если она не является действительно значимым фактором. Фактически, это принятие решения — потерять переменную или часть данных.
3. Оценка средним, медианой, модой
Замена пропущенных значений средним, медианой или модой — грубый способ работы с ними. В зависимости от ситуации, например, если вариация данных невелика, или эта переменная мало влияет на выходную, такая грубая аппроксимация, возможно, приемлема и даст удовлетворительные результаты.
Давайте посчитаем точность в случае замены средним:
4. Прогнозирование
Прогнозирование — самый сложный метод замены пропущенных значений. Он включает следующие подходы: kNN-оценка, rpart и mice.
4.1. kNN-оценка
DMwR::knnImputation использует метод k ближайших соседей для замены пропущенных значений. Проще говоря, kNN-оценка делает следующее. Для каждого данного, требующего замены, определяется k ближайших точек на основании евклидового расстояния, и рассчитывается их взвешенное (по расстоянию) среднее.
Преимущество состоит в том, что можно заменить все пропущенные значения во всех переменных одним вызовом функции. Она принимает в качестве аргумента весь набор данных, и можно даже не указывать, какую переменную хотите заменить. Однако, при замене нужно не допустить включения в расчет выходной переменной.
Давайте оценим точность:
Средняя абсолютная ошибка в процентах (mape) улучшилась примерно на 39% по сравнению с заменой средним. Неплохо.
4.2 rpart
Ограничение DMwR::knnImputation состоит в том, что иногда эту функцию не получится использовать, если пропущены значения факторной переменной. И rpart , и mice подходят для такого случая. Преимущество rpart в том, что достаточно хотя бы одной переменной, не содержащей NA .
Теперь воспользуемся rpart для замены пропущенных значений вместо kNN . Для того, чтобы обработать факторную переменную, нужно установить method=class при вызове rpart() . Для числовых значений будем использовать method=anova . В этом случае также надо убедиться, что в обучении rpart не используется выходная переменная ( medv ).
Посчитаем точность для ptratio:
Средняя абсолютная ошибка в процентах (mape) улучшилась еще примерно на 30% по сравнению с kNN-оценкой. Очень хорошо.
Точность для rad:
Ошибка неправильной классификации — 25%. Неплохо для факторной переменной!
4.3 mice
mice — сокращение от Multivariate Imputation by Chained Equations (многомерная оценка цепными уравнениями) — пакет R, предоставляющий сложные функции для работы с пропущенными значениями. Он использует немного необычный способ оценки в два шага: mice() для построения модели и complete() для генерации данных. Функция mice(df) создает несколько полных копий df, каждая со своей оценкой пропущенных данных. Функция complete() возвращает один или несколько наборов данных, набор по умолчанию будет первым. Давайте посмотрим, как заменить rad и ptratio:
Рассчитаем точность ptratio:
Средняя абсолютная ошибка в процентах (mape) улучшилась еще примерно на 48% по сравнению с rpart. Отлично!
Рассчитаем точность для rad:
Ошибка неправильной классификации сократилась до 15%, т.е. 6 из 40 наблюдений. Это значительное улучшение по сравнению с 25% для rpart.
Хотя в целом понятно, насколько хорош каждый метод, этого недостаточно, чтобы утверждать наверняка, который из них лучше или хуже. Но все они точно достойны вашего внимания, когда понадобится решать задачу замены пропущенных значений.
Источник