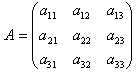Способ заполнения двумерного массива

Pascal-Паскаль

Программирование. Двумерные массивы Pascal-Паскаль

• Скачено бесплатно: 18605
• Куплено: 414

• Pascal-Паскаль->Программирование. Двумерные массивы Pascal-Паскаль

Программирование. Двумерные массивы Pascal-Паскаль

Двумерные массивы Паскаля – матрицы

Двумерный массив в Паскале трактуется как одномерный массив, тип элементов которого также является массивом (массив массивов). Положение элементов в двумерных массивах Паскаля описывается двумя индексами. Их можно представить в виде прямоугольной таблицы или матрицы.

Рассмотрим двумерный массив Паскаля размерностью 3*3, то есть в ней будет три строки, а в каждой строке по три элемента:

Каждый элемент имеет свой номер, как у одномерных массивов, но сейчас номер уже состоит из двух чисел – номера строки, в которой находится элемент, и номера столбца. Таким образом, номер элемента определяется пересечением строки и столбца. Например, a 21 – это элемент, стоящий во второй строке и в первом столбце.

Описание двумерного массива Паскаля.

Существует несколько способов объявления двумерного массива Паскаля.

Мы уже умеем описывать одномерные массивы, элементы которых могут иметь любой тип, а, следовательно, и сами элементы могут быть массивами. Рассмотрим следующее описание типов и переменных:

Пример описания двумерного массива Паскаля

Мы объявили двумерный массив Паскаля m, состоящий из 10 строк, в каждой из которых 5 столбцов. При этом к каждой i -й строке можно обращаться m [ i ], а каждому j -му элементу внутри i -й строки – m [ i , j ].

Определение типов для двумерных массивов Паскаля можно задавать и в одной строке:

Обращение к элементам двумерного массива имеет вид: M [ i , j ]. Это означает, что мы хотим получить элемент, расположенный в i -й строке и j -м столбце. Тут главное не перепутать строки со столбцами, а то мы можем снова получить обращение к несуществующему элементу. Например, обращение к элементу M [10, 5] имеет правильную форму записи, но может вызвать ошибку в работе программы.

Основные действия с двумерными массивами Паскаля

Все, что было сказано об основных действиях с одномерными массивами, справедливо и для матриц. Единственное действие, которое можно осуществить над однотипными матрицами целиком – это присваивание. Т.е., если в программе у нас описаны две матрицы одного типа, например,

то в ходе выполнения программы можно присвоить матрице a значение матрицы b ( a := b ). Все остальные действия выполняются поэлементно, при этом над элементами можно выполнять все допустимые операции, которые определены для типа данных элементов массива. Это означает, что если массив состоит из целых чисел, то над его элементами можно выполнять операции, определенные для целых чисел, если же массив состоит из символов, то к ним применимы операции, определенные для работы с символами.

Ввод двумерного массива Паскаля.

Для последовательного ввода элементов одномерного массива мы использовали цикл for, в котором изменяли значение индекса с 1-го до последнего. Но положение элемента в двумерном массиве Паскаля определяется двумя индексами: номером строки и номером столбца. Это значит, что нам нужно будет последовательно изменять номер строки с 1-й до последней и в каждой строке перебирать элементы столбцов с 1-го до последнего. Значит, нам потребуется два цикла for , причем один из них будет вложен в другой.

Рассмотрим пример ввода двумерного массива Паскаля с клавиатуры:

Пример программы ввода двумерного массива Паскаля с клавиатуры

Двумерный массив Паскаля можно заполнить случайным образом, т.е. использовать функцию random (N), а также присвоить каждому элементу матрицы значение некоторого выражения. Способ заполнения двумерного массива Паскаля выбирается в зависимости от поставленной задачи, но в любом случае должен быть определен каждый элемент в каждой строке и каждом столбце.

Вывод двумерного массива Паскаля на экран.

Вывод элементов двумерного массива Паскаля также осуществляется последовательно, необходимо напечатать элементы каждой строки и каждого столбца. При этом хотелось бы, чтобы элементы, стоящие в одной строке, печатались рядом, т.е. в строку, а элементы столбца располагались один под другим. Для этого необходимо выполнить следующую последовательность действий (рассмотрим фрагмент программы для массива, описанного в предыдущем примере):

Пример программы вывода двумерного массива Паскаля

Замечание (это важно!): очень часто в программах студентов встречается ошибка, когда ввод с клавиатуры или вывод на экран массива пытаются осуществить следующим образом: readln (a), writeln (a), где а – это переменная типа массив. При этом их удивляет сообщение компилятора, что переменную этого типа невозможно считать или напечатать. Может быть, вы поймете, почему этого сделать нельзя, если представите N кружек, стоящих в ряд, а у вас в руках, например, чайник с водой. Можете вы по команде «налей воду» наполнить сразу все кружки? Как бы вы ни старались, но в каждую кружку придется наливать отдельно. Заполнение и вывод на экран элементов массива также должно осуществляться последовательно и поэлементно, т.к. в памяти ЭВМ элементы массива располагаются в последовательных ячейках.

Представление двумерного массива Паскаля в памяти

Элементы абстрактного массива в памяти машины физически располагаются последовательно, согласно описанию. При этом каждый элемент занимает в памяти количество байт, соответствующее его размеру. Например, если массив состоит из элементов типа integer , то каждый элемент будет занимать по два байта. А весь массив займет S^2 байта, где S – количество элементов в массиве.

А сколько места займет массив, состоящий из массивов, т.е. матрица? Очевидно: S i^S j , где S i — количество строк, а S j – количество элементов в каждой строке. Например, для массива типа

потребуется 12 байт памяти.

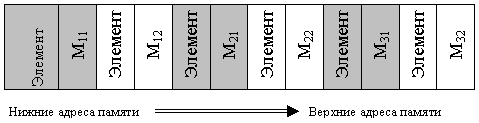
Как будут располагаться в памяти элементы этого массива? Рассмотрим схему размещения массива M типа matrix в памяти.

Под каждый элемент M [i,j] типа integer выделяется две ячейки памяти. Размещение в памяти осуществляется «снизу вверх». Элементы размещаются в порядке изменения индекса, что соответствует схеме вложенных циклов: сначала размещается первая строка, затем вторая, третья. Внутри строки по порядку идут элементы: первый, второй и т.д.

Как мы знаем, доступ к любой переменной возможен, только если известен адрес ячейки памяти, в которой хранится переменная. Конкретная память выделяется для переменной при загрузке программы, то есть устанавливается взаимное соответствие между переменной и адресом ячейки. Но если мы объявили переменную как массив, то программа «знает» адрес начала массива, то есть первого его элемента. Как же происходит доступ ко всем другим элементам массива? При реальном доступе к ячейке памяти, в которой хранится элемент двумерного массива, система вычисляет ее адрес по формуле:

где Addr – фактический начальный адрес, по которому массив располагается в памяти; I , J – индексы элемента в двумерном массиве; SizeElem – размер элемента массива (например, два байта для элементов типа integer ); Cols – количество элементов в строке.

Выражение SizeElem * Cols *( I -1)+ SizeElem *( J -1) называют смещением относительно начала массива.

Сколько памяти выделяется для массива?

Рассмотрим не столько вопрос о том, сколько памяти выделяется под массив (это мы разобрали в предыдущем разделе), а о том, каков максимально допустимый размер массива, учитывая ограниченный объем памяти.

Для работы программы память выделяется сегментами по 64 Кбайт каждый, причем как минимум один из них определяется как сегмент данных. Вот в этом-то сегменте и располагаются те данные, которые будет обрабатывать программа. Ни одна переменная программы не может располагаться более чем в одном сегменте. Поэтому, даже если в сегменте находится только одна переменная, описанная как массив, то она не сможет получить более чем 65536 байт. Но почти наверняка, кроме массива в сегменте данных будут описаны еще некоторые переменные, поэтому реальный объем памяти, который может быть выделен под массив, находится по формуле: 65536- S , где S – объем памяти, уже выделенный под другие переменные.

Зачем нам это знать? Для того чтобы не удивляться, если при компиляции транслятор выдаст сообщение об ошибке объявления слишком длинного массива, когда в программе встретит описание (правильное с точки зрения синтаксиса):

Вы уже знаете, что, учитывая двухбайтовое представление целых чисел, реально можно объявить массив с количеством элементов равным 65536/2 –1=32767. И то лишь в том случае, если других переменных не будет. Двумерные массивы должны иметь еще меньшие границы индексов.

Примеры решения задач с двумерными массивами Паскаля

Задача: Найти произведение ненулевых элементов матрицы.

Решение:

• Для решения данной задачи нам потребуются переменные: матрица, состоящая, например, из целочисленных элементов; P – произведение элементов, отличных от 0; I , J – индексы массива; N , M – количество строк и столбцов в матрице.
• Входными данными являются N , M – их значения введем с клавиатуры; матрица – ввод матрицы оформим в виде процедуры, заполнение матрицы осуществим случайным образом, т.е. с помощью функции random ().
• Выходными данными будет являться значение переменной P (произведение).
• Чтобы проверить правильность выполнения программы, необходимо вывести матрицу на экран, для этого оформим процедуру вывода матрицы.
• Ход решения задачи:

обсудим сначала выполнение основной программы, реализацию процедур обговорим чуть позже:

• введем значения N и M ;
• Введем двумерный массив Паскаля, для этого обращаемся к процедуре vvod ( a ), где а – матрица;
• Напечатаем полученную матрицу, для этого обращаемся к процедуре print ( a );
• Присвоим начальное значение переменной P =1;
• Будем последовательно перебирать все строки I от 1-й до N -й, в каждой строке будем перебирать все столбцы J от 1-го до M -го, для каждого элемента матрицы будем проверять условие: если a ij ? 0, то произведение P будем домножать на элемент a ij ( P = P * a ij );
• Выведем на экран значение произведения ненулевых элементов матрицы – P ;

А теперь поговорим о процедурах.

Замечание (это важно!) Параметром процедуры может быть любая переменная предопределенного типа, это означает, что для передачи в процедуру массива в качестве параметра, тип его должен быть описан заранее. Например :

Вернемся теперь к нашим процедурам.

Процедура ввода матрицы называется vvod , параметром процедуры является матрица, причем она должна быть, как результат, передана в основную программу, следовательно, параметр должен передаваться по ссылке. Тогда заголовок нашей процедуры будет выглядеть так:

Для реализации вложенных циклов в процедуре нам потребуются локальные переменные-счетчики, например, k и h . Алгоритм заполнения матрицы уже обсуждался, поэтому не будем его повторять.

Процедура вывода матрицы на экран называется print , параметром процедуры является матрица, но в этом случае она является входным параметром, следовательно, передается по значению. Заголовок этой процедуры будет выглядеть следующим образом:

И вновь для реализации вложенных циклов внутри процедуры нам потребуются счетчики, пусть они называются так же – k и h . Алгоритм вывода матрицы на экран был описан выше, воспользуемся этим описанием.

Пример программы двумерного массива Паскаля

Программирование

Исходники Pascal (127)

Справочник

Справочник по паскалю: директивы, функции, процедуры, операторы и модули по алфавиту

Источник

Двумерные массивы

Объявление, ввод и вывод двумерного массива

Для хранения прямоугольных таблиц, состоящих из строк и столбцов, необходимо использовать массивы, каждый элемент которых является строкой массивом чисел. Если считать, что одна строка — это vector , то двумерный массив — это вектор элементов типа vector , то есть его нужно объявлять как vector > . При этом по стандарту языка C++ до 2011 года, в конце определения между двумя символами “ a таким образом, то a[i] будет одномерным массивом, который обычно считают строкой. То есть a[i][j] будет j-м элементом i-й строки. Например, двумерный массив из 3 строк и 4 столбцов можно записать в виде:

Чтобы создать массив из n строк и m столбцов, можно объявить его указанным образом:

Затем необходмио размер “внешнего” массива изменить на n (сделать n строк в таблице):

Затем размер каждого массива-строки необходимо изменить на m. Это можно сделать циклом:

Заметим, что строки могут иметь разную длину, например, можно сделать массив в форме “лесенки”, где каждая строка будет содержать на один элемент больше предыдущей:

Но если необходимо создать прямоугольный массив, то можно сразу же при объявлении задать его размер, если воспользоваться конструктором для вектора с параметрами. Первый параметр — размер вектора, второй необязательный параметр — значение, которым будут инциализированы элементы вектора. Тогда в качестве первого параметра можно передать n, а в качестве второго параметра можно явно указать конструктор, который создает вектор из m элементов типа int : vector (m) . Итак, создать прямоугольную таблицу размером n×m можно в одну строку:

Если вложенному вызову конструктора (для строки) передать второй параметр, то все элементы массива будут заполнены переданным значением вместо нуля. int A[n] создает в памяти одномерный массив: набор пронумерованных элементов, идущих в памяти последовательно. К каждому элементу массива можно обратиться, указав один индекс — номер этого элемента. Но можно создать и двумерный массив следующим образом: int A[n][m] . Данное объявление создает массив из n объектов, каждый из которых в свою очередь является массивом типа int [m] . Тогда A[i] , где i принимает значения от 0 до n-1 будет в свою очередь одним из n созданных обычных массивов, и обратиться к элементу с номером j в этом массиве можно через A[i][j] .

Подобные объекты (массивы массивов) также называют двумерными массивами. Двумерные массивы можно представлять в виде квадратной таблицы, в которой первый индекс элемента означает номер строки, а второй индекс – номер столбца. Например, массив A[3][4] будет состоять из 12 элементов и его можно записать в виде —>

Для считывания, вывода на экран и обработки двумерных массивов необходимо использовать вложенные циклы. Первый цикл – по первому индексу (то есть по всем строкам), второй цикл – по второму индексу, то есть по всем элементам в строках (столбцам). Например, вывести на экран двумерный массив в виде таблицы, разделяя элементы в строке одним пробелом можно следующим образом:

А считать двумерный массив с клавиатуры можно при помощи еще более простого алгоритма (массив вводится по строкам, то есть в порядке, соответствующему первому примеру):

Обработка двумерного массива

Обработка двумерных массивов производится аналогичным образом. Например, если мы хотим записать в массив таблицу умножения, то есть присвоить элементу a[i][j] значение i * j , это можно сделать следующим образом при помощи вложенных циклов:

Рассмотрим более сложную задачу и несколько способов ее решения. Пусть дан квадратный двумерный массив размером n×n. Необходимо элементам, находящимся на главной диагонали проходящей из левого верхнего угла в правый нижний (то есть тем элементам a[i][j] , для которых i == j ) присвоить значение 1 , элементам, находящимся выше главной диагонали – значение 0, элементам, нахощящимся ниже главной диагонали – значение 2. То есть получить такой массив (пример для n == 4 ):

Рассмотрим несколько способов решения этой задачи. Элементы, которые лежат выше главной диагонали – это элементы a[i][j] , для которых i , а для элементов ниже главной диагонали i > j . Таким образом, мы можем сравнивать значения i и j и по ним определять значение a[i][j] . Получаем следующий алгоритм:

Данный алгоритм плох, поскольку выполняет одну или две инструкции if для обработки каждого элемента. Если мы усложним алгоритм, то мы сможем обойтись вообще без условных инструкций.

Сначала заполним главную диагональ, для чего нам понадобится один цикл:

Затем заполним значением 0 все элементы выше главной диагонали, для чего нам понадобится в каждой из строк с номером i присвоить значение элементам a[i][j] для j = i+1 , . n-1 . Здесь нам понадобятся вложенные циклы:

Аналогично присваиваем значение 2 элементам a[i][j] для j = 0 , . i-1 :

Можно также внешние циклы объединить в один и получить еще одно, более компактное решение:

Многомерные массивы

Если необходимо хранить в массиве величину, зависящую от трёх параметров-индексов, например, a[i][j][k] , то для представления такого массива нужно использовать вектор, элементами которого будут двумерные векторы, то есть

Их можно рассматривать как “трёхмерные” таблицы, но проще думать о таких массивах, просто как о величине, определяемой тремя параметрами-индексами.

Их тоже можно создавать в одну строку, добавив ещё один уровень вложенности конструкторов. Например, пусть требуется создать массив размера x×y×z, то есть первый индекс будет принимать значения от 0 до x-1, второй индекс от 0 до y-1, третий индекс от 0 до z-1. Можно использовать такое объявление:

Передача двумерных массивов в функцию

Передавать двумерные массивы в функцию всегда лучше по ссылке, т.е. добавляя знак “&” перед идентификатором параметра. Например:

Это обязательно делать в случае, когда функция должна модифицировать передаваемый массив, если же функция не модифицирует передаваемый массив, всё равно лучше массив передавать по ссылке, так как в этом случае не производится копирование массива (если массив передается по значению, то создается копия массива, что требует дополнительного времени).

Форматирование чисел при выводе

Допустим, мы заполним массив таблицей умножения: a[i][j] = i * j как в примере в начале раздела. Если мы теперь попробуем вывести этот массив на экран, разделяя элементы в строке одним пробелом, то из-за того, что числа имеют различную длину столбцы таблицы окажутся неровными:

Для того, чтобы получить ровные столбцы необходимо, выводить числа так, чтобы одно выводимое число имело ширину, например, ровно в 3 символа, а “лишние” позиции были бы заполнены пробелами. Тогда получится следующая таблица:

Для того, чтобы выводимое число или строка имело ровно заданную ширину, необходимо перед выводом его на экран для потока cout вызвать метод width с параметром 3 . Данный метод устанавливает ширину поля для выводимого значения. Получим следующую программу для вывода:

Заметим, что мы теперь не выводим пробел после каждого числа, поскольку мы добавили этот пробел к ширине выводимого поля. Функция width действует однократно, только на следующее выводимый в поток значение, поэтому ее нужно вызывать перед каждым выводом числа на экран.

Внимание! Если выводимое число или строка имеет большую длину, чем это было установлено функцией width , то это число или строка будут выведены полностью, а не будет обрезано до указанного значения. То есть предпочтительней вывести результат некрасиво, нежели неверно.

Источник