1.4. Замена переменной в определённом интеграле
Для определенного интеграла справедливы все типы замен, что и для неопределенного интеграла, но иногда её проводить нельзя (о чём позже). Ну а основная новизна состоит в том, как поменять пределы интегрирования при замене? В примерах ниже я постараюсь привести такие типы замен, которые не встречались ранее:
Пример 5
Вычислить определенный интеграл 
Во-первых, замечаем, что отрезок 
входит в область определения подынтегральной функции (подкоренное выражение больше нуля вообще при любом 
).
И главный вопрос здесь не в определённом интеграле, а в том, какую подобрать замену. Смотрим в Таблицу интегралов (см. Приложения) и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: 
. Но есть одна неувязочка: в табличном интеграле под корнем 
, а в нашем – «икс» в четвёртой степени. И из этих рассуждений следует идея замены – неплохо бы нашу четвертую степень превратить в квадрат. Это реально.
Сначала готовим интеграл к замене:
(прерываем решение для промежуточных действий)
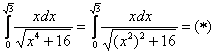
Из вышеуказанных соображений совершенно естественно напрашивается замена: 
, после чего в знаменателе будет всё хорошо: 
.
Выясняем, во что превратится оставшаяся часть 
подынтегрального выражения, для этого навешиваем дифференциалы на обе части: 
раскрываем дифференциал слева: 
и выражаем нужный нам кусок: 
По сравнению с заменой в неопределенном интеграле, у нас добавляется дополнительный этап: находим новые переделы интегрирования.
Это достаточно просто. Смотрим на нашу замену 
и старые пределы интегрирования 
, 
.
Сначала подставляем в 
нижний предел интегрирования, то есть, ноль: 
,
затем подставляем верхний предел интегрирования – корень из трёх: 
И всего-то лишь…. Завершаем решение: 
(1) В соответствии с проведённой заменой, записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу 
лучше оставить за скобками, чтобы она не мешалась в дальнейших вычислениях. Справа отчеркиваем линию с указанием новых пределов интегрирования 
– это подготовка для применения формулы Ньютона-Лейбница.
(3) Используем формулу Ньютона-Лейбница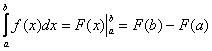 
и упрощаем результат по известной формуле.
И особенно приятно, что никаких обратных замен проводить не нужно.
А сейчас пара интегралов для самостоятельного решения. Какие замены проводить – постарайтесь догадаться самостоятельно.
Пример 6
Вычислить определенные интегралы
а)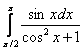 
, б) 
Решения и ответы в конце книги. Приложение Тригонометрические таблицы в помощь, в изучаемой теме этот справочный материал требуется довольно часто.
И теперь обещанный момент о правомерности замены. В определённой ситуации её проводить нельзя! Так, интеграл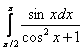 
, казалось бы, разрешим с помощью универсальной тригонометрической подстановки 
, однако верхний предел интегрирования («пи») не входит в область определения этого тангенса и поэтому данная подстановка нелегальна! Таким образом, функция-«замена» должна быть непрерывна во всех точках отрезка 
интегрирования.
Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Источник
Метод замены переменной в неопределённом интеграле
Суть метода замены переменной
Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.
Вводится новая переменная, назовём её t . Например,
- в интеграле
можем ввести новую переменную ; - в интеграле можем ввести новую переменную ;
- в интеграле можем ввести новую переменную .
;
;Далее dx определеяем как дифференциал по переменной t . После этого интеграл можно найти по таблице интегралов. Заменив обратно t на функцию от x , находим данный интеграл окончательно.
Прежде чем перейти к подробным решениям примеров, следует привести теорему, в которой обобщаются перечисленные выше действия.
Теорема. Пусть функция 
определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
(1)
Формула (1) называется формулой замены переменной в неопределённом интеграле.
Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.
Применяем замену переменной вместе
Надо полагать, вы уже держите перед собой домашние задания и готовы применять к ним приёмы по аналогии с теми, которые мы ниже рассмотрим. При этом не обойтись без преобразований выражений. Для этого потребуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Пример 1. Найти неопределённый интеграл методом замены переменной:
Решение. Производим замену x − 1 = t ; тогда x = t + 1 . Отсюда dx = dt . По формуле (1)
Возвращаясь к переменной x , окончательно получаем
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.
Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.
Пример 2. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим 
. Отсюда 
.
По формуле (1)
.
Возвращаясь к переменной x, окончательно получаем
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Если трудно уследить, куда в процессе решения примера 2 делись 
и 
, это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.
Пример 3. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим 
, откуда 
и 
.
Тогда 
, в свою очередь 
.
Заменяем переменную и получаем:
,
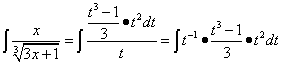
где степени при t складываются. Продолжаем преобразования и получаем:
Приводим дроби к общему знаменателю и возвращаемся к переменной x. Решаем и получаем ответ:
Применить замену переменной самостоятельно, а затем посмотреть решение
Пример 4. Найти неопределённый интеграл методом замены переменной:
.
Пример 5. Найти неопределённый интеграл методом замены переменной:
.
Пример 6. Найти неопределённый интеграл методом замены переменной:
.
Снова применяем замену переменной вместе
Пример 7. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим 
, откуда 
, 
, 
.
Тогда
(не забываем о правиле дифференцирования сложной функции).
Заменяем переменную и получаем:
.
Возвращаясь к переменной х, получаем ответ:
.
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Пример 8. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим 
, откуда 
, 
.
Заменяем переменную и получаем:
Подставляя вместо t его выражение через x получаем ответ:
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Кому лишь смутно понятно или совсем не понятно, как преобразуются выражения в примере 5, пожалуйста, повторите из курса элементарной (школьной) математики действия с корнями, степенями и дробями!
И если вы ещё не открыли в новых окнах пособия Действия со степенями и корнями и Действия с дробями, то сделайте это сейчас!
Пример 9. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим 
, тогда 
.
Заменяем переменную и получаем:
Решение с переменной t получено с использованием формулы 21 из таблицы интегралов.
Подставляя вместо t его выражение через x получаем ответ:
.
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Источник
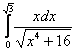
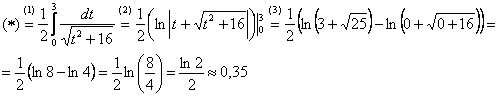
