Способ замены плоскостей проекций треугольник

58. Способ замены плоскостей проекций

Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.

Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.

Рассмотрим решение четырех исходных задач способом замены плоскостей проекций.

1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.

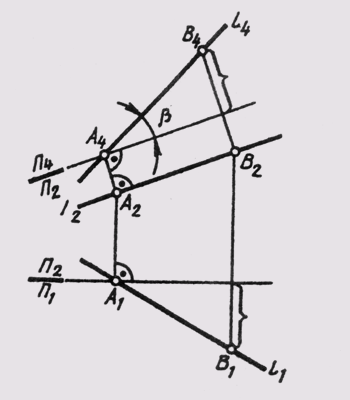
Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П₄, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П₁_|_П₂ перейти к системе П₄ _|_ П₁ или П₄ _|_ П₂. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П₁ _|_ П₄, причем П₄ || l. Новые линии связи A₁A₄ и В₁В₄проведены

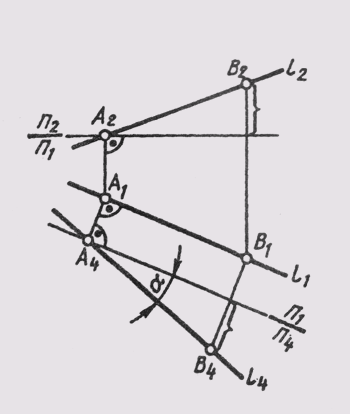
перпендикулярно новой оси —П₁/П₄ параллельной горизонтальной проекции l₁.

Новая проекция прямой дает истинную величину А₄В₄отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций (а = L₁П₁). Угол наклона прямой к фронтальной плоскости проекций (b = L₁П₂) можно определить, построив изображение прямой на другой дополнительной плоскости П4_|_П₂ (рис. 109).

2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.

Чтобы на новой плоскости проекций изображение прямой было точкой (см. § 10), новую плоскость проекций нужно расположить перпендикулярно данной прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П₄_|_ П₁. (рис. 110), а фронталь f— на П₄_|_ П₂

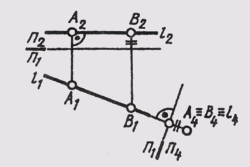
Если требуется построить вырожденную в точку проекцию прямой общего положения, то для преобразования чертежа потребуется произвести две последовательные замены плоскостей проекций. На рис. 111 исходный чертеж прямой l (А,В) преобразован следующим образом: сначала построено изображение прямой на плоскости П₄_|_ П₂, расположенной параллельно самой прямой l. В системе плоскостей П₂_|_ П₄, прямая заняла положение линии l уровня (А₂А₄ _|_П₂/П₁;

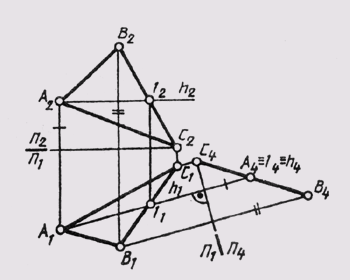
П₄ _|_П₅, причем вторая новая плоскость проекций П₅ перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П₄, то на плоскости П₅ получаем изображение прямой в виде точки (А₅ = B₅ = l₅).

3. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение.

Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из основных плоскостей проекций. Это возможно сделать, если учесть, что направление ортогонального проецирования на новую плоскость проекций должно совпадать с направлением соответствующих линий уровня данной плоскости общего положения. Тогда все линии этого уровня на новой плоскости проекций изобразятся точками, которые и дадут «вырожденную» в прямую проекцию плоскости (см. § 47).

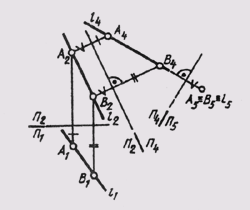
На рис. 112 дано построение нового изображения плоскости 0 (ABC) в системе плоскостей П₄ _|_П₁. Для этого в плоскости 0 построена горизонталь h(A, 1), и новая плоскость проекций П₄ расположена перпендикулярно горизонтали h. Графическое решение третьей исходной задачи приводят к построению изображения плоскости в виде прямой линии, угол наклона которой к новой оси проекции П₁/П₄, определяет угол наклона а плоскости Q(ABC) к горизонтальной плоскости проекций (а = Q ^ П₁).

Построив изображение плоскости общего положения в системе П₂ _|_П₄, (П₄ расположить перпендикулярно фронтали плоскости),

можно определить угол наклона Р этой плоскости к фронтальной плоскости проекций.

4. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня.

Решение этой задачи позволяет определить величину плоских фигур.

Новую плоскость проекций нужно расположить параллельно заданной плоскости. Если исходное положение плоскости было фронтально проецирующим, то новое изображение строят в системе и П₂ _|_П₄, а если горизонтально проецирующим, то в системе П₁ _|_П₄. Новая ось проекций будет расположена параллельно вырожденной проекции проецирующей плоскости (см. § 47). На рис. 113 построена новая проекция А₄В₄С₄горизонтально проецирующей плоскости Sum (ABC) на плоскости П₄ _|_П₁

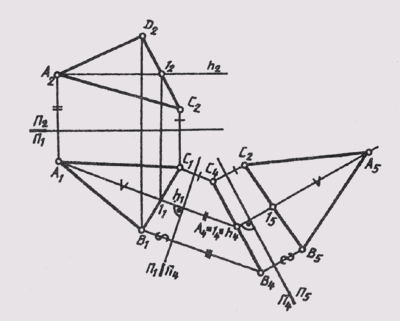
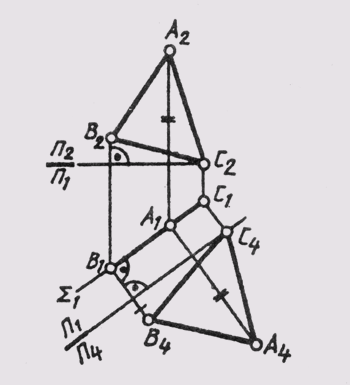
Если в исходном положении плоскость занимает общее положение, а нужно получить изображение ее как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно задачу 3; а затем задачу 4. При первой замене плоскость становится проецирующей, а при второй — плоскостью уровня (рис. 114).

В плоскости А(DEF) проведена горизонталь h (D — 1). По отношению к горизонтали проведена первая ось П₁ / П₄ _|_h₁. Вторая новая ось

проекций параллельна вырожденной проекции плоскости, а новые линии связи — перпендикулярны вырожденной проекции плоскости. Расстояния для построения проекций точек на плоскости П₅ нужно замерить на плоскости П₁от оси П₁ / П₂и откладывать по новым линиям связи от новой оси П₄ /П₅. Проекция D₅E₅F₅треугольника DEF конгруэнтна самому треугольнику ABC.

С применением способа замены плоскостей можно решать ряд других задач как самостоятельных, так и отдельных частей задач, включающих большой объем графических решений.

Источник

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Решение пространственных задач на комплексном чертеже значительно упрощается, если интересующие нас элементы фигуры занимают частное положение.

Переход от общего положения геометрической фигуры к частному выполняется следующим способом: введением дополнительных плоскостей проекций, расположенных либо параллельно, либо перпендикулярно рассматриваемому геометрическому элементу.

Сущность способа заключается в том, что пространственное положение объекта не изменяют, а вводят новую, дополнительную плоскость проекций, расположенную таким образом, чтобы интересующие нас элементы фигуры или весь объект целиком проецировался на неё в удобном для решения задачи положении. При этом новая плоскость проекций должна быть перпендикулярна к одной из имеющихся плоскостей проекций. В результате образуется новая система взаимно перпендикулярных плоскостей проекций, заменяющая прежнюю.

На рис. 54 в систему плоскостей проекций введем новую плоскость проекций . Новой осью проекций будет . Заметим, что координаты Z точек А и В в плоскостях и будет одна и та же. И кроме того, если новую ось выберем параллельно проекции прямой , то на плоскости проекций проекция проектируется в натуральную величину прямой АВ.

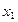
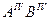
ПЕРЕВОД ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ В ПОЛОЖЕНИЕ ПРЯМОЙ УРОВНЯ

(т.е. параллельно новой плоскости проекций )

Для преобразования прямой АВ в прямую уровня (рис. 55) вводят новую плоскость проекций так, чтобы ось проекций была параллельна проекции (рис. 54), затем откладывают на новой плоскости проекций от оси ( ) координаты Z точек и , равные координатам Z точек и .

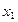
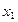
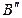
Новая проекция прямой дает натуральную величину отрезка АВ и угол наклона прямой к плоскости проекций .

ПЕРЕВОД ПРЯМОЙ УРОВНЯ В ПРОЕЦИРУЮЩЕЕ ПОЛОЖЕНИЕ

(т.е. перпендикулярно плоскости проекций)

Чтобы на новой плоскости проекций изображение прямой уровня преобразовалось в точку (рис. 56), надо эту плоскость расположить перпендикулярно данной прямой, т.е. провести на комплексном чертеже ось проекций перпендикулярно направлению проекции прямой на общую плоскость проекций. Горизонталь будет иметь своей проекцией точку на плоскости .

Для построения вырожденной в точку проекции прямой общего положения необходимо последовательно решить две предыдущие задачи: на рис. 57 представлено такое решение.

ПЕРЕВОД ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩЕЕ

Известно, что если одна плоскость перпендикулярна другой, то она должна содержать прямую, перпендикулярную этой плоскости. В качестве такой прямой можно взять прямую уровня, например, горизонталь, как это показано на рис. 58.

Переведем горизонталь h в проецирующее положение, вводя новую плоскость проекций . Поскольку проекция плоскости АВС на плоскости вырождена ыв прямую, она будет служить геометрическим местом всех точек, принадлежащих этой плоскости. Проецируем точки плоскости на , беря их координаты Z с плоскости .

ПЕРЕВОД ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТИ В ПОЛОЖЕНИЕ ПЛОСКОСТИ УРОВНЯ

Решение этой задачи позволяет определить натуральную величину плоской фигуры (рис. 59.).

Пусть задана фронтально-проецирующая плоскость . Вводим новую плоскость проекций , параллельную . Новая ось проекций по этой причине будет расположена параллельно , т.е. в системе плоскостей проекций плоскость займет положение плоскости уровня, а треугольник АВС будет проецироваться на плоскость в натуральную величину.

Если в исходном положении плоскость занимает общее положение, а нужно получить её изображение как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно две предыдущие задачи. При первой замене плоскость становится проецирующей (вырождается в линию), а при второй – плоскостью уровня (рис. 60 – не приведён). Расстояние для построения проекций точек на плоскости нужно брать с плоскости , отмеряя их от оси проекций .

Источник