Способ замены переменной для решения интегралов

Интегрирование методом замены переменной

Метод замены переменной

С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.

Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x , переходим к другой переменной, которую обозначим как t . При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x ( t ) , или t = t ( x ) . Например, x = ln t , x = sin t , t = 2 x + 1 , и т.п. Нашей задачей является подобрать такую зависимость между x и t , чтобы исходный интеграл либо свелся к табличному, либо стал более простым.

Основная формула замены переменной

Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f ( x ) и дифференциала dx : . Пусть мы переходим к новой переменной t , выбрав некоторое соотношение x = x ( t ) . Тогда мы должны выразить функцию f ( x ) и дифференциал dx через переменную t .

Чтобы выразить подынтегральную функцию f ( x ) через переменную t , нужно просто подставить вместо переменной x выбранное соотношение x = x ( t ) .

Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt .

На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t ( x ) . Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′ ( x ) – это производная t по x , то
.

Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x – это функция от t .
(2) ,
где t – это функция от x .

Важное замечание

В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x . Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое-либо выражение.

В качестве примера рассмотрим табличный интеграл
.

Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.

В последнем примере нужно учитывать, что при переходе к переменной интегрирования x , дифференциал преобразуется следующим образом:
.
Тогда
.

В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.

Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2). Положим t = x 2 + x . Тогда
;
;

.

Примеры интегрирования заменой переменной

1) Вычислим интеграл
.
Замечаем, что (sin x )′ = cos x . Тогда

.
Здесь мы применили подстановку t = sin x .

2) Вычислим интеграл
.
Замечаем, что . Тогда

.
Здесь мы выполнили интегрирование заменой переменной t = arctg x .

3) Проинтегрируем
.
Замечаем, что . Тогда

. Здесь, при интегрировании, произведена замена переменной t = x 2 + 1 .

Линейные подстановки

Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b ,
где a и b – постоянные. При такой замене дифференциалы связаны соотношением
.

Примеры интегрирования линейными подстановками

B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции.
.
ln 2 – это постоянная. Вычисляем интеграл.

.

C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.

.

D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.

.
Интегрируем, применяя метод замены переменной .

.
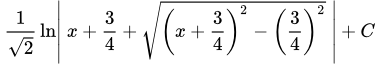
Ранее мы получили формулу
.
Отсюда
.
Подставив это выражение, получим окончательный ответ.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 06-09-2015

Источник

Метод замены переменной в неопределённом интеграле

Суть метода замены переменной

Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.

Вводится новая переменная, назовём её t . Например,

• в интеграле можем ввести новую переменную ;
• в интеграле можем ввести новую переменную ;
• в интеграле можем ввести новую переменную .

Далее dx определеяем как дифференциал по переменной t . После этого интеграл можно найти по таблице интегралов. Заменив обратно t на функцию от x , находим данный интеграл окончательно.

Прежде чем перейти к подробным решениям примеров, следует привести теорему, в которой обобщаются перечисленные выше действия.

Теорема. Пусть функция определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула

(1)

Формула (1) называется формулой замены переменной в неопределённом интеграле.

Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.

Применяем замену переменной вместе

Надо полагать, вы уже держите перед собой домашние задания и готовы применять к ним приёмы по аналогии с теми, которые мы ниже рассмотрим. При этом не обойтись без преобразований выражений. Для этого потребуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Пример 1. Найти неопределённый интеграл методом замены переменной:

Решение. Производим замену x − 1 = t ; тогда x = t + 1 . Отсюда dx = dt . По формуле (1)

Возвращаясь к переменной x , окончательно получаем

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.

Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.

Пример 2. Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим . Отсюда
.
По формуле (1)

.

Возвращаясь к переменной x, окончательно получаем

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Если трудно уследить, куда в процессе решения примера 2 делись и , это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.

Пример 3. Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , откуда и .

Тогда , в свою очередь .

Заменяем переменную и получаем:

,

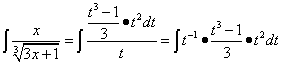
где степени при t складываются. Продолжаем преобразования и получаем:

Приводим дроби к общему знаменателю и возвращаемся к переменной x. Решаем и получаем ответ:

Применить замену переменной самостоятельно, а затем посмотреть решение

Пример 4. Найти неопределённый интеграл методом замены переменной:

.

Пример 5. Найти неопределённый интеграл методом замены переменной:

.

Пример 6. Найти неопределённый интеграл методом замены переменной:

.

Снова применяем замену переменной вместе

Пример 7. Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , откуда , , .

Тогда

(не забываем о правиле дифференцирования сложной функции).

Заменяем переменную и получаем:

.

Возвращаясь к переменной х, получаем ответ:

.

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 8. Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , откуда , .

Заменяем переменную и получаем:

Подставляя вместо t его выражение через x получаем ответ:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Кому лишь смутно понятно или совсем не понятно, как преобразуются выражения в примере 5, пожалуйста, повторите из курса элементарной (школьной) математики действия с корнями, степенями и дробями!

И если вы ещё не открыли в новых окнах пособия Действия со степенями и корнями и Действия с дробями, то сделайте это сейчас!

Пример 9. Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , тогда
.

Заменяем переменную и получаем:

Решение с переменной t получено с использованием формулы 21 из таблицы интегралов.

Подставляя вместо t его выражение через x получаем ответ:

.

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Источник
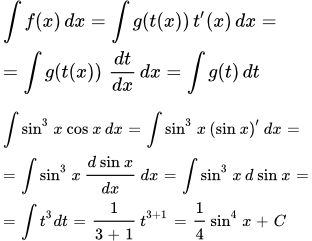