Способ замены одной плоскости

Основы способа замены плоскостей проекцией

Основы способа замены плоскостей проекцией

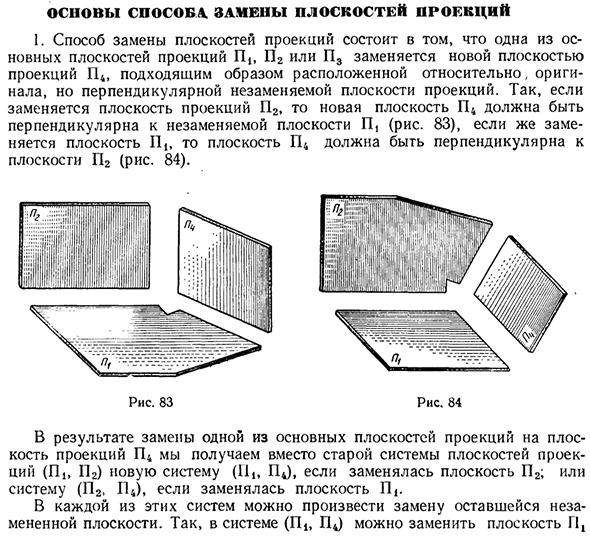
• Основы метода. Замена плана проекции 1. Способ замены плоскости проекции заключается в замене одной из основных плоскостей проекции П1П2 или П3 новой плоскостью проекции Г14, которая правильно расположена относительно исходной плоскости проекции, но перпендикулярно плоскости проекции, которую нельзя заменить. это.

• Следовательно, при замене плоскости P2 проекции новая плоскость P4 перпендикулярна неизменяемой плоскости P (рисунок 83), а при замене плоскости P | плоскость P4 перпендикулярна плоскости P2 (рисунок 84). Рис. 83 Рисунок 84 Замена одной из основных плоскостей проекции на плоскость проекции П4 приводит к новой системе (11 bП ^, если плоскость 112 была заменена, плоскость П | вместо старой системы плоскостей проекции (ПпП2) Даёт систему (П2, Г14).

В каждой из этих систем вы можете заменить оставшиеся невидимые плоскости. Людмила Фирмаль

Следовательно, в системе (Pinj, плоскость Г1Ж С новой плоскостью P5, перпендикулярной неизменяемой плоскости P4, и системой (P2, P4) можно заменить плоскость P2 плоскостью P5, перпендикулярной P4. Затем получите новую систему (P4, P5). Последовательно вводя новые проекционные плоскости P4, P5, Pv, …, вы можете получить систему проекционных плоскостей, где этот оригинал занимает удобное место для решения конкретной задачи.

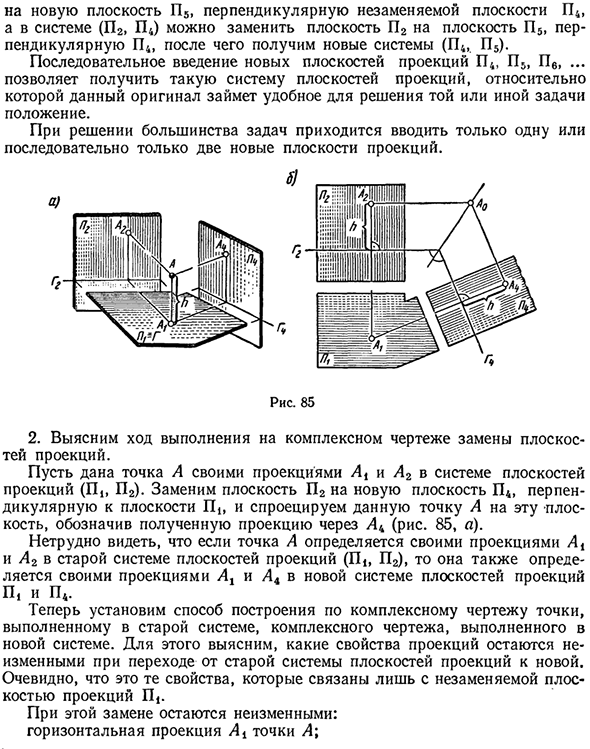
Чтобы решить большинство проблем, вам нужно ввести только одну или две новые плоскости проекции. Рисунок 85 2. Проверить ход выполнения сложного чертежа при замене проекционной плоскости. Точка A задается проекциями At и A2 системы проекционных плоскостей (||, 22).

Замените плоскость P2 новой плоскостью P4, перпендикулярной плоскости P |, и спроецируйте эту точку A на эту плоскость, показывая проекцию, полученную Ak (рис. 85, а). Если точка A определяется проекциями A и A2 старой системы плоскостей проекции (Pi, EY), легко увидеть, что она также определяется проекциями Ax и A4 новых систем плоскостей проекции P и P4.

Затем установите, как построить в соответствии со сложными чертежами точек, созданными в старой системе, и сложными чертежами, созданными в новой системе. Для этого изучите, какие свойства проекции не меняются при переходе плоскости проекции из старой системы в новую. Очевидно, это те свойства, которые связаны только с незаменимой проекционной плоскостью П |.

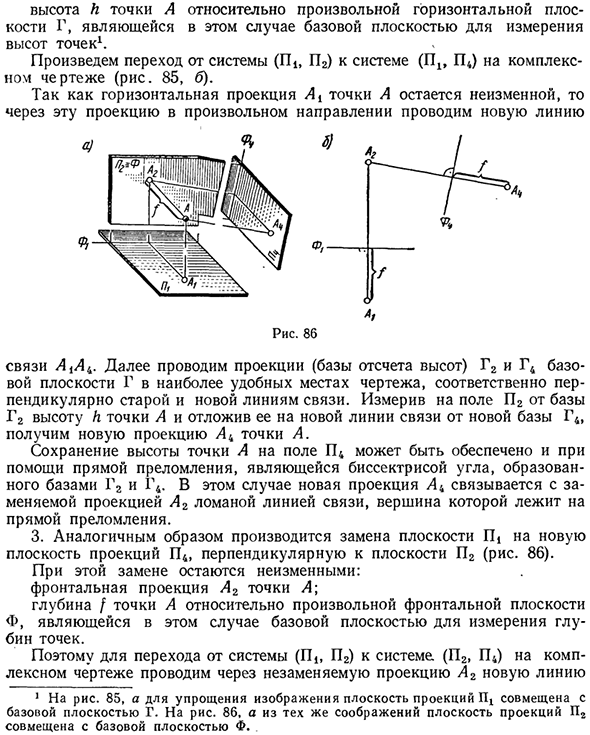
Эта замена не меняет их. Горизонтальная проекция точки А. Высота h точки A относительно произвольной горизонтальной плоскости G. В этом случае это базовая плоскость для измерения высоты точки G1. Переход от системы (П1П2) к системе (П1ЭП4) со сложными чертежами (рис. 85, б). Поскольку горизонтальная проекция Ai точки A не изменяется, через эту проекцию в любом направлении проводится новая линия Рис. 86 Подключите A% Ak.

Затем проекции базовой плоскости G (см. Базовую высоту) G2 и G4 выполняются в наиболее удобном месте на чертеже, перпендикулярном старой и новой линиям связи, соответственно. Измерение высоты h точки A в поле P2 от базы G2 и размещение ее на новой линии связи от новой базы G4 дает новую проекцию A4 точки A.

Сохранение высоты точки A на поле P4 также может быть достигнуто с помощью прямого преломления, которое является биссектрисом угла, образованного основаниями G2 и G4. В этом случае новый выступ 44 соединен с замененным выступом Ar прерывистой линией, а его вершина находится на линии преломления. 3.

Аналогичным образом плоскость rij заменяется новой плоскостью проекции P4, перпендикулярной плоскости P2 (рис. 86). Эта замена не меняет их. Фронтальная проекция Ar точки A; Глубина / точка A для любого ребра фронтальной плоскости. В этом случае базовая плоскость для измерения глубины точки.

Поэтому для перехода от системы (P1e P2) к системе (P2, P4) в сложном чертеже нарисуйте новую линию на незаменимой проекции A2. На фиг.8 плоскость P1 проекции совмещена с базовой плоскостью G, чтобы упростить изображение. 86, и по той же причине плоскость P2 проекции совмещена с базовой плоскостью F.

• Общение в направлении AzAit мы выбрали. Затем базовая плоскость проекции (базовая опорная глубина) j и Ф4 выполняются перпендикулярно старой и новой линиям связи соответственно. Далее измеряем поле Jit от базы Φ. Если глубина f точки A находится на новой линии связи от нового основания Ф4, получается проекция Ai точки A.

Легко видеть, что построение исходной проекции профиля из двух заданных проекций, горизонтальной и передней, по существу заменяет плоскость rif проекции на плоскость P3, перпендикулярную плоскостям P4 и P2 (рис. 18). см). 4. Произведенная замена плоскости проекции показывает, что одна из этих плоскостей проекции П1П2 или П3 может быть в любой момент заменена на плоскость П4, перпендикулярную неизменяемой плоскости проекции.

Объединяет, как создать новый проект со сложными чертежами. Людмила Фирмаль

Точка трансформации при замене одной из плоскостей проекции одним правилом. Чтобы создать новую проекцию точки на сложном чертеже при замене одной из плоскостей проекции, необходимо сделать следующее: Нарисуйте новую линию связи (в направлении, соответствующем заданным условиям) через незаменимую проекцию точек.

Выполняет стандарт расстояния (высоты, глубины или широты) перпендикулярно старой и новой линиям связи в сменном и новом полях, соответственно. Измерьте расстояние замененной проекции точки от основания заменяемого поля и поместите его на новую линию связи от основания нового поля. Это правило применяется к последовательному выполнению двух или более замен.

Следовательно, для точки А, если плоскость П2 заменяется плоскостью П4, перпендикулярной плоскости Пt (рис. 87, 85), а затем необходимо заменить плоскость rij плоскостью П5, перпендикулярной плоскости П4, выполняется последнее изменение. Поля, которые необходимо учитывать при rij заменяется, поле P4 не заменяется, а поле P5 является новым.

Поле P2 не участвует в этой замене. Линии связи в полях P1 и P4 считаются старыми линиями связи, а линии связи в полях P4 и P5 считаются новыми линиями связи. Базовая плоскость параллельна незаменимой плоскости проекции, поэтому, если первая плоскость заменяется горизонтальной плоскостью Γ, вторая плоскость заменяется горизонтально спроецированной плоскостью 2.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Способ замены плоскостей проекций

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

1. Сушность способа замены плоскостей

2. Применение способа замены плоскостей к отрезку прямой

3. Применение способа замены плоскостей к плоской фигуре

1. Сушность способа замены плоскостей

Этот способ заключается в том, что заданную систему плос­костей проек­ций заменяют новой системой так, что предмет (прямая или плоскость), не изменяя своего положения в про­странстве, оказывается в частном положении относительно новой системы плоскостей проекций. Плоскости проекций обра­зуют новую ортогональную систему.

В зависимости от условий задачи приходится заменять либо одну из заданных плоскостей проекций, либо обе, если заменой одной плоскости проекций не удается получить необходимого расположения проецируемого предмета относительно плоско­сти проекций.

Возьмем в системе плоскостей проекций Н и V произвольную точку А и построим ее прямоугольные проекции а и а’ (рис. 60). Заменим фронтальную плоскость V новой плос­костью V 1 , перпендикулярной плоскости Н, т. е. от системы плоскостей перейдем к системе с новой осью jx 1 . Спроеци-

ровав точку А на плоскость V 1 получим новую проекцию а1′. Горизонтальная проекция а точки А принадлежит обеим систе­мам плоскостей проекций. Из построений видно, что a 1 ‘ aXi = Aa = a ‘ ax = zA , т. е. при замене плоскости V плоскостью V 1 , пер­пендикулярной плоскости Н, координата проецируемой точки остается без изменения.

Для получения чертежа совмещаем все три плоскости – Н, V к V 1 – в одну плоскость (рис. 60). В новой системе проекции a и a ‘ находятся на линии проекционной связи, пер­пендикулярной к новой оси x 1 . При этом расстояние aXi a 1 ‘ = axa ‘= zA .

Заменив горизонтальную плоскость проекций Н новой плос­костью H 1 , перпендикулярной плоскости V, от системы плоскостей проекций переходят к новой системе (рис. 61).

Построив проекции точки А в обеих системах, замечаем, что координата у остается неизменной. На чертеже отрезок oXla 1 = axa = yA , что и позволяет строить новую проекцию а1 заданной точки А на перпендикуляре, проведенном из а’ к но­вой оси о x 1 .

Последовательная замена двух плоскостей проекций показа­на на рис. 62. Сначала плоскость V заменена плоскостью V 1 перпендикулярной плоскости H , и построена новая проекция а1 точки А. Затем плоскость Н заменена плоскостью Н1 перпен­дикулярной плоскости V 1 , и построена новая проекция а1. Та­ким образом совершен последовательный переход от системы плоскостей проекций к системе, а затем к системе.

В системе плоскостей проекциями точки А будут а< и а1′, после­довательное построение которых определяется неизменностью координаты z в системе плоскостей и координаты y 1 в системе плоскостей

Решение задач данным методом рассмотрим на двух при­мерах.

2. Применение способа замены плоскостей

к отрезку прямой

Пример 1. Определить длину отрезка АВ прямой по его проекциям ab и а’Ь’ (рис. 63).

Задача решается путем замены одной из заданных плоско­стей проекций новой плоскостью проекций, параллельной отрез­ку АВ. На новую плоскость отрезок проецируется в истинную величину.

При замене плоскости V плоскостью V 1 , параллельной отрез­ку АВ, новую ось ох1 проводят параллельно горизонтальной про­екции ab ( рис .63 а). Опустив из точек а и b перпендикуляры на ось ох1 и отложив на них aXla 1 ‘= axa ‘ и bXib 1 ‘ = bxb ‘, получа­ют новую проекцию а1′ b ‘1, равную отрезку АВ, а также угол ан, равный углу наклона прямой к плоскости Н.

На рис. 63 б дано решение той же задачи путем замены плоскости Н плоскостью Н1, параллельной отрезку АВ. В этом случае ось ох1 располагаем параллельно фронтальной проек­ции a ‘ b ‘ и аналогично предыдущему получаем проекцию а1 b 1 равному заданному отрезку, и угол α v , раный углу наклона прямой к плоскости V .

3. Применение способа замены плоскостей

к плоской фигуре

Пример 2. Определить величину и форму треугольника АВС по его проекциям abc и а’ b ‘с’ (рис. 64).

Треугольник прое­циру­ет­ся без искажения на па­рал­лельную ему плос­кость про­екций. В общем случае од­ной заменой плос­костей проек­ций этого добиться невоз­можно, поэто­му после­дова­тель­но заменяют две плос­кости проек­ций.

Сначала заменяют плос-кость V плоскостью V 1 пер-пен­ди­ку­­лярной плоскости треу­гольника. Для этого в плоскости тре­уголь­ни­ка проводят горизонталь AD и пер­пендикулярно к ней рас­пола­га­ют плоскость V 1 . На чертеже построение сводится к прове­де­нию оси х1, перпендикулярной горизонтальной проек­ции ad горизонтали. Горизонталь AD проецируется на плос­кость V 1 в точку a 1 ‘ ≡ d 1 , а треугольник — в отрезок b 1 c 1 .

Затем заменяют плоскость Н плоскостью Н1 параллельной плоскости треугольника ABC . Ось ох2 будет параллельна проек­ции b 1 ‘а1’с1’, а проекция b 1 а1с1 отобразит истинную величину треугольника.

Источник