Способ замены двух плоскостей проекций

Способ замены плоскостей проекций состоит в том, что проецируемый объект остается неподвижным, а одна из плоскостей проекций П₁, П₂ или П₃ заменяется новой, расположенной так, чтобы проецируемый объект по отношению к новой плоскости занял частное положение. При этом каждая новая плоскость проекций должна быть перпендикулярна незаменяемой плоскости проекций. Кроме того, на новые плоскости проекций объект проецируется ортогонально. Таким образом, при решении задач способом замены плоскостей проекций необходимо выполнять следующие условия:

• каждая новая система должна представлять собой систему двух взаимно перпендикулярных плоскостей;

• на новые плоскости объект проецируется ортогонально;

• расстояние от точки до незаменяемой плоскости сохраняется.

Чтобы определить натуральную величину отрезка способом замены плоскостей проекций (рис. 128, 129), необходимо выбрать новую плоскость проекций таким образом, чтобы в новой системе плоскостей проекций отрезок занял положение линии уровня:

1. Зафиксировать положение системы плоскостей П₁/П₂ с помощью оси x₁₂⊥A₁A₂.

2. Определить положение плоскости П₄ с помощью оси x₁₄. Чтобы отрезок в системе плоскостей П₁/П₄ занял положение линии уровня, ось x₁₄ проводится параллельно горизонтальной проекции отрезка [A₁B₁].

3. Ортогонально спроецировать отрезок [AB] на плоскость П4. Для этого линии связи проводят перпендикулярно оси x₁₄, затем от оси x₁₄ откладывают расстояние до незаменяемой плоскости – координаты z точек A и B.

Чтобы преобразовать плоскость общего положения в проецирующую, новую плоскость проекций строят перпендикулярно линии уровня этой плоскости.

Рассмотрим преобразование плоскости общего положения α(ABC) во фронтально-проецирующую плоскость (рис. 130). Для решения этой задачи способом замены плоскостей проекций необходимо выполнить замену плоскости П₂ на П₄:

1. Зафиксировать положение системы плоскостей проекций П₁/П₂ с помощью оси x₁₂⊥A₁A₂;

2. Построить в плоскости α(ABC) фронталь;

3. В соответствии с теоремой о проекциях прямого угла, построить новую ось x₂₄⊥f₁(C₂ 1₂);

4. Ортогонально спроецировать фронталь на плоскость П₄. Для этого провести линию связи (12,14) перпендикулярно x₂₄ и отложить от оси x₂₄ расстояние до незаменяемой плоскости – координату y точек 1 и С. Поскольку y₁=y_c, фронталь в системе плоскостей проекций П₁/П₄ займет положение горизонтально-проецирующей прямой.

5. Проекция плоскости α(ABC) на П₄ определится фронталью и точкой A. В системе плоскостей проекций П₂/П₄ плоскость α(ABC) займет горизонтально-проецирующее положение. Проекцию точки B можно построить по координате y_b или на пересечении следа плоскости α(ABC) на П₄ с линией связи (B₂B₄).

При решении некоторых задач необходимо определить натуральную величину плоских объектов. Любой плоский объект проецируется без искажения на параллельную ему плоскость. Чтобы определить натуральную величину грани призмы способом замены плоскостей проекций, необходимо (рис. 131):

1. Зафиксировать положение системы плоскостей П₁/П₂ с помощью оси x₁₂=A₂D₂ K₂;.

2. Плоскость грани ABCD занимает горизонтально-проецирующее положение, поэтому выполняется замена плоскости П₂ на плоскость П₄, параллельную грани ABCD. Новую ось x₁₄ проводят параллельно A₁B₁C₁D₁.

3. Ортогонально спроецировать все вершины призмы на плоскость П4. Для этого проводят линии связи перпендикулярно оси x₁₄, затем от оси x₁₄ откладывают расстояние до незаменяемой плоскости – координаты z вершин призмы. Координаты z вершин нижнего основания A, D и K равны нулю, следовательно, точки , и лежат на оси x₁₄. Координаты z вершин верхнего основания равны (A₂B₂).

4. В системе плоскостей П₁/П₄ грань ABCD занимает положение фронтальной плоскости уровня, следовательно, проецируется на П₄ в натуральную величину.

Источник

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Решение пространственных задач на комплексном чертеже значительно упрощается, если интересующие нас элементы фигуры занимают частное положение.

Переход от общего положения геометрической фигуры к частному выполняется следующим способом: введением дополнительных плоскостей проекций, расположенных либо параллельно, либо перпендикулярно рассматриваемому геометрическому элементу.

Сущность способа заключается в том, что пространственное положение объекта не изменяют, а вводят новую, дополнительную плоскость проекций, расположенную таким образом, чтобы интересующие нас элементы фигуры или весь объект целиком проецировался на неё в удобном для решения задачи положении. При этом новая плоскость проекций должна быть перпендикулярна к одной из имеющихся плоскостей проекций. В результате образуется новая система взаимно перпендикулярных плоскостей проекций, заменяющая прежнюю.

На рис. 54 в систему плоскостей проекций введем новую плоскость проекций . Новой осью проекций будет . Заметим, что координаты Z точек А и В в плоскостях и будет одна и та же. И кроме того, если новую ось выберем параллельно проекции прямой , то на плоскости проекций проекция проектируется в натуральную величину прямой АВ.

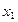
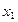
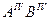
ПЕРЕВОД ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ В ПОЛОЖЕНИЕ ПРЯМОЙ УРОВНЯ

(т.е. параллельно новой плоскости проекций )

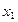
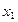
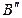
Для преобразования прямой АВ в прямую уровня (рис. 55) вводят новую плоскость проекций так, чтобы ось проекций была параллельна проекции (рис. 54), затем откладывают на новой плоскости проекций от оси ( ) координаты Z точек и , равные координатам Z точек и .

Новая проекция прямой дает натуральную величину отрезка АВ и угол наклона прямой к плоскости проекций .

ПЕРЕВОД ПРЯМОЙ УРОВНЯ В ПРОЕЦИРУЮЩЕЕ ПОЛОЖЕНИЕ

(т.е. перпендикулярно плоскости проекций)

Чтобы на новой плоскости проекций изображение прямой уровня преобразовалось в точку (рис. 56), надо эту плоскость расположить перпендикулярно данной прямой, т.е. провести на комплексном чертеже ось проекций перпендикулярно направлению проекции прямой на общую плоскость проекций. Горизонталь будет иметь своей проекцией точку на плоскости .

Для построения вырожденной в точку проекции прямой общего положения необходимо последовательно решить две предыдущие задачи: на рис. 57 представлено такое решение.

ПЕРЕВОД ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩЕЕ

Известно, что если одна плоскость перпендикулярна другой, то она должна содержать прямую, перпендикулярную этой плоскости. В качестве такой прямой можно взять прямую уровня, например, горизонталь, как это показано на рис. 58.

Переведем горизонталь h в проецирующее положение, вводя новую плоскость проекций . Поскольку проекция плоскости АВС на плоскости вырождена ыв прямую, она будет служить геометрическим местом всех точек, принадлежащих этой плоскости. Проецируем точки плоскости на , беря их координаты Z с плоскости .

ПЕРЕВОД ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТИ В ПОЛОЖЕНИЕ ПЛОСКОСТИ УРОВНЯ

Решение этой задачи позволяет определить натуральную величину плоской фигуры (рис. 59.).

Пусть задана фронтально-проецирующая плоскость . Вводим новую плоскость проекций , параллельную . Новая ось проекций по этой причине будет расположена параллельно , т.е. в системе плоскостей проекций плоскость займет положение плоскости уровня, а треугольник АВС будет проецироваться на плоскость в натуральную величину.

Если в исходном положении плоскость занимает общее положение, а нужно получить её изображение как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно две предыдущие задачи. При первой замене плоскость становится проецирующей (вырождается в линию), а при второй – плоскостью уровня (рис. 60 – не приведён). Расстояние для построения проекций точек на плоскости нужно брать с плоскости , отмеряя их от оси проекций .

Источник