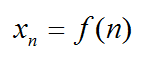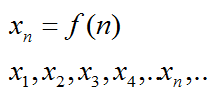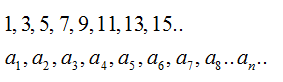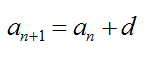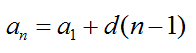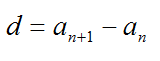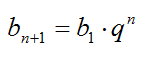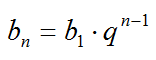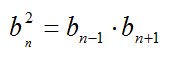Способ задания натуральных чисел

Числовые последовательности для чайников: определение, формулы

• 12 января 2021 г.
• 10 минут
• 79 198
• 2

По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.

Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.

Последовательности чисел

Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной.

Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.

Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.

Что такое числовая последовательность?

Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:

• для каждого натурального числа существует элемент данного множества;
• это число является номером элемента и обозначает позицию данного элемента в последовательности;
• для любого элемента последовательности можно указать следующий за ним элемент.

Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.

Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.

На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.

Какие бывают последовательности

• постоянную, или монотонную последовательность: 1, 1, 1, 1, 1.
• возрастающую последовательность, в которой каждый следующий элемент больше предыдущего
• убывающую последовательность, в которой каждый следующий элемент меньше предыдущего

Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.

Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.

Арифметическая прогрессия

Посмотрим на числа:

Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.

Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:

Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.

Сумма первых n членов прогрессии вычисляется по формуле:

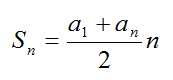
Также африфметическая прогрессия обладает характреристическим свойством:

Геометрическая прогрессия

Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:

Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:

Сумма первых n членов прогрессии:

Характеристическое свойство геометрической прогрессии:

Способы задания последовательностей

Последовательность можно задать несколькими способами:

1. Аналитически или, проще говоря, формулой.
2. Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
3. Описательно, простым перечислением всех элементов последовательности.

Предел последовательности

Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.

Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.

Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.

Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел.

Что нужно помнить, вычисляя пределы последовательностей

Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.

1. Последовательность может иметь только один предел.
2. Если последовательность имеет предел, то она ограничена. Обратное верно не всегда!
3. Если члены некоторой последовательности zn заключены между соответствующими членами двух последовательностей xn, yn, сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу.
4. Предел постоянной последовательности равен ее постоянному.
5. Если две последовательности x и y равны между собой, то пределы этих последовательностей также равны между собой, если они существуют.
6. Если каждый член сходящейся последовательности не превосходит соответствующего члена другой сходящейся последовательности, то и предел первой не превосходит предела второй.
7. Предел суммы (разности) двух последовательностей равен сумме (разности) их пределов. При условии, что обе последовательности имеют пределы.
8. Предел произведения двух последовательностей, имеющих пределы, существует и равен произведению пределов последовательностей.
9. Постоянный множитель можно выносить за знак предела.
10. Предел частного двух последовательностей, имеющих пределы, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.

Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором.

Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.

Источник

Числовые последовательности. Способы их задания.

Урок № 32 АЛГЕБРА

Учитель математики, первой категории Гаун Ольга Викторовна. Восточно-Казахстанская область Глубоковский район КГУ «Черемшанская средняя школа»

Тема: Числовая последовательность и способы ее задания

Основные цели и задачи урока

Образовательная: разъяснить учащимся смысл понятий «последовательность», «n-ый член последовательности»; познакомить со способами задания последовательности.

Развивающа я: развитие навыков логического мышления; развитие вычислительных навыков; развитие культуры устной речи, развитие коммуникативности и сотрудничества. Воспитательная : воспитание наблюдательности, привитие любви и интереса к предмету.

Ожидаемые результаты освоения темы

В ходе урока приобретут новые знания о числовых последовательностях и способах ее задания. Научатся находить верное решение, составлять алгоритм решения и пользоваться им при решении заданий. Путем исследования обнаружат их некоторые свойства. Вся работа сопровождается слайдами. Применение ИКТ даст возможность провести урок оживленно, выполнить большой объем работы, со стороны ребят будет искренний интерес и эмоциональное восприятие. Одарённые ученики выступят с сообщением о числах Фибоначчи и о золотом сечении. Универсальные учебные действия, на формирование которых направлен образовательный процесс: умение работать в паре, развивать логическое мышление, умение анализировать, исследовать, делать выводы, отстаивать свою точку зрения. Обучить навыкам общения и сотрудничества. Использование данных технологий способствует развитию у обучающихся универсальных способов деятельности, опыта творческой деятельности, компетентности, коммуникабельности.

Ключевые идеи урока

Новые подходы в преподавании и обучении

— обучение тому, как обучаться

Обучение критическому мышлению

Обучение талантливых и одарённых детей

Изучение новой темы

Наглядный (презентация), словесный (беседа, объяснение, диалог), практический.

Формы организации учебной деятельности уч-ся

фронтальная; парная; индивидуальная.

(Приветствие учащихся, определение отсутствующих, проверка готовности учащихся к уроку, организация внимания).

«Числа управляют миром»,- говорили древнегреческие ученые. «Все есть число». Согласно их философскому мировоззрению, числа управляют не только мерой и весом, но также явлениями, происходящими в природе, и являются сущностью гармонии, царствующей в мире. Сегодня на уроке мы продолжим работать с числами.

Введение в тему, изучение нового материала.

Давайте проверим ваши логические способности. Я называю несколько слов, а вы должны продолжить:

– январь, февраль, март…;

– Алиев, Гордеева, Грибачева… (список класса);

Вывод: Это последовательности, то есть некоторый упорядоченный ряд чисел или понятий, когда каждое число или понятие стоит строго на своем месте. Итак, тема урока – последовательность.

Сегодня мы будем говорить о видах и составляющих числовых последовательностей, а также о способах их задания. Последовательности будем обозначать так: (аn), (bn), (сn) и т.д.

А сейчас я предлагаю вам первое задание: перед вами некоторые числовые последовательности и словестное описание этих последовательностей. Вам необходимо найти закономерность каждого ряда и соотнести с описанием. (показать с помощью стрелки) (Взаимопроверка)

Рассмотренные нами ряды и есть примеры числовых последовательностей .

Элементы, образующие последовательность, называются членами последовательности и называются соответственно первым, вторым, третьим,… n — ным членами последовательности. Обозначают члены последовательности так а ₁ ; а ₂ ; а ₃ ; а ₄ ; … а _n ; где n – номер , под которым данное число находится в последовательности.

На экране записаны последовательности:
( На перечисленных последовательностях отрабатываются форма записи члена последовательности a _n , и понятия предыдущего и последующего членов ) .
3; 6; 9; 12; 15; 18;…
5, 3, 1, -1.
1, 4, 9, 16 ,…
–1; 2; –3; 4; –5; 6; …
3; 3; 3; 3; …; 3; … .

Назовите а ₁ для каждой последовательности, а ₃ и т.д. А смогли бы вы продолжить каждый из этих рядов? Что для этого необходимо знать?

Давайте разберем с вами еще такие понятия как последующий и предыдущий .

Виды последовательностей
( на перечисленных выше последовательностях отрабатывается навык определять виды последовательностей )
1) Возрастающая – если каждый член меньше следующего за ним, т.е. a _n a _{n +1.}
2) Убывающая – если каждый член больше следующего за ним, т.е. a _n > a _{n +1} .
3) Бесконечная
4) Конечная
5) Знакочередующаяся
6) Постоянная (стационарная)

Попробуйте дать определение каждому виду и охарактеризуйте каждую из предложенных последовательностей.

Задания для устной работы

Назовите в последовательности 1; 1/2; 1/3; 1/4; 1/5; … 1/n; 1/(n+1) члены а ₁ ; а ₄ ; а ₁₀ ; а _n ;

Является ли последовательность четырёхзначных чисел конечной? (да)

Назовите её первый и последний члены. (Ответ: 1000; 9999)

Является ли последовательностью запись чисел 2; 4; 7; 1; -21; -15; …? (нет, так как нельзя по первым шести членам обнаружить какую-нибудь закономерность)

Физпауза (тоже связана с темой сегодняшнего урока: звездное небо, планеты солнечной системы…в чем связь?)

Способы задания последовательностей
1) словесный – задание последовательности описанием;
2) аналитический – формулой n -го члена;
3) графический – с помощью графика;
4) рекуррентный – любой член последовательности, начиная с некоторого, выражается через предыдущие
Сегодня на уроке мы разберем первых два способа. Итак, словестный способ. Может быть кто-нибудь из вас попробует задать какую-либо последовательность?

( Например: Составьте последовательность нечетных натуральных чисел . Охарактеризуйте эту последовательность: возрастающая, бесконечная)
Аналитический способ: с помощью формулы n-ого члена последовательности.

Формула общего члена позволяет вычислить член последовательности с любым заданным номером. Например, если х _n =3n+2, то

х ₄₅ =3 . 45+2=137 и т.д. Так каково преимущество аналитического способа перед словестным ?

А я вам предлагаю следующее задание: даны формулы задания некоторых последовательностей и сами последовательности, образованных по этим формулам. В этих последовательностях пропущены некоторые члены. Ваша задача, работая в парах , заполнить пропуски.

Самопроверка (на слайде появляется правильный ответ)

Представление творческого проекта «Числа Фибоначчи» ( опережающее задание )

Сегодня мы познакомимся со знаменитой последовательностью:

1, 1, 2, 3, 5, 8, 13, 21, …, (Слайд) Каждое число, начиная с третьего, равно сумме двух предшествующих. Этому ряду натуральных чисел, имеющему своё историческое название – ряд Фибоначчи, присуща своя логика и красота. Леонардо Фибоначчи (1180-1240). Крупный итальянский математик, автор «Книги абака». Эта книга несколько веков оставалась основным хранилищем сведений по арифметике и алгебре. Именно по трудам Л. Фибоначчи вся Европа осваивала арабские цифры, систему счета, а также практическую геометрию. Они оставались настольными учебниками, чуть ли не до эпохи Декарта (а это уже 17 век!).

Наверное, вы не совсем поняли какова связь между спиралью и рядом Фибоначчи. Поэтому я покажу, как она получается .

Если мы построим рядом два квадрата со стороной 1,затем набольшей стороне равной 2 другой, затем на большей стороне, равной 3 еще квадрат так до бесконечности…Потом в каждом квадрате, начиная с меньшего, построим четверть дуги, то получим спираль, о которой идет речь в фильме.

На самом деле практическое применение знаний, полученных на этом уроке в реальной жизни достаточно велико. Перед вами несколько задач из разных научных областей.

Задача 1. Продолжи последовательности чисел:

16, 15, 18, … (17, 20, 19)

1, 2, 2, 4, 8, … (32, 256, 8192)

33, 31, 32, … (30, 31, 29)

Задача 2. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день?

(Ответы учащихся записываются на доске: 500, 530, 560, 590, 620).

Задача 3. Автомобиль, двигаясь со скоростью 1 м/с за каждую последующую секунду изменял свою скорость на 0,6 м/с. Какую скорость он будет иметь спустя 10 секунд?

Задача 4. Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих. Через сколько дней заболеют все ученики нашей школы (300 человек)? (Через 4 дня).

Задача 5 . Сколько появится бактерий куриной холеры за 10 часов, если одна бактерия делится пополам каждый час?
Задача 6 . Курс воздушных ванн начинают с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин? ( 10)

Задача 7 . При свободном падении тело проходит в первую секунду 4,8 м, а в каждую следующую на 9,8 м больше. Найдите глубину шахты, если свободно падающее тело достигло ее дна через 5 с после начала падения.

Задача 8 . Гражданина К. осталось завещание. Он в первый месяц истратил 1000$, а каждый последующий месяц истратил на 500$ больше. Сколько денег было завещано гражданину К., если их хватит на 1 год безбедной жизни? (45000)

Быстро и без ошибок решать такие задачи нам позволит изучение следующих тем этой главы «Прогрессии».

Домашнее задание: стр.66 №151, 156, 157

Творческое задание: сообщение о треугольнике Паскаля

Подведение итого. Рефлексия. (оценка «приращения» знаний и достижения целей)

Источник