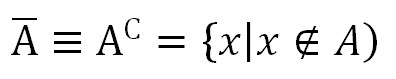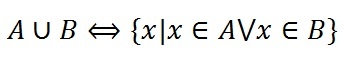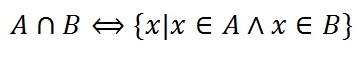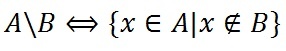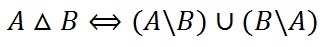- Как составить диаграмму Эйлера-Венна
- Диаграмма Эйлера-Венна — что из себя представляет, где используется
- Принципы построения, как изобразить множества
- Дополнение множества
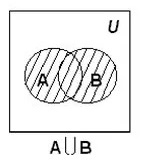
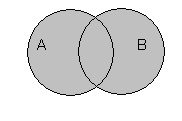
- Объединение множеств
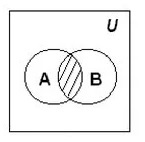
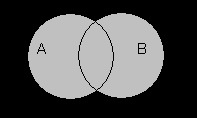
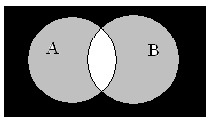
- Пересечение множеств
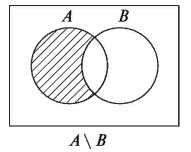
- Разность множеств
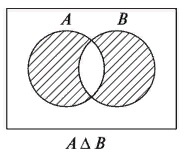
- Симметричная разность множеств
- Использование диаграмм Эйлера-Венна для доказательства логических равенств
- Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
- Как логические операции связаны с теорией множеств
- Примеры задач с решением
- Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
Как составить диаграмму Эйлера-Венна
Диаграмма Эйлера-Венна — что из себя представляет, где используется
Диаграмма Эйлера-Венна представляет собой геометрическую схему, предназначенную для представления моделей множеств и схем их взаимосвязей.
Благодаря данной диаграмме, приводят наглядное объяснение разных фактов о множествах. При таком методе универсальное множество представляют в виде прямоугольника, а для изображения подмножества используют круги. Широкое применение диаграммы Эйлера-Венна нашли в таких дисциплинах, как математика, логика, менеджмент, финансы и другие прикладные направления.
Способы отражения отношений между множествами ранее отличались. Джон Венн применял в качестве обозначения множеств замкнутые фигуры, а Эйлер – круги.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Диаграммы Эйлера-Венна представляют собой важный частный случай кругов, которые изображал Эйлер. На диаграммах представлены все 2 n комбинаций n свойств, что является конечной булевой алгеброй. Если n = 3, на диаграмме, как правило, изображают три круга с центрами, которые расположены в углах равностороннего треугольника, и совпадающими радиусами, ориентировочно равными длине сторон этого многоугольника.
Принципы построения, как изобразить множества
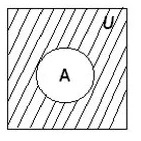
Построить диаграмму Эйлера-Венна – значит, составить большой прямоугольник, представляющий универсальное множество U, и разместить внутри него замкнутые фигуры в качестве обозначения множеств.
В том случае, когда требуется строить на диаграмме не более трех множеств, целесообразно использовать круги. Для изображения свыше четырех множеств применяют эллипсы. Пересечение фигур соответствует максимально общему случаю, согласно условиям задачи, и изображается должным образом на диаграмме.
Если предположить, что диаграмма содержит круг, обозначающий множество А, его центральная часть будет отражать истинность выражения А, а область вне круга – обозначать ложь. Те области, которые соответствуют истинным значениям, заштриховывают, что является отражением логической операции на диаграмме.
Согласно алгебре логики, конъюнкция множеств А и В соответствует истине в том случае, когда истинны оба эти множества. При этом на диаграмме отмечают участок пересечения множеств.
Применяя диаграммы Эйлера-Венна, доказывают любые алгебраические законы с помощью их графического изображения. Алгоритм построения:
- изображение диаграммы с заштрихованными множествами, которые представлены в левой части выражения;
- чертеж другой диаграммы с заштрихованными множествами, расположенными в правой части уравнения;
- сравнение заштрихованных областей на диаграммах: если это одна и та же область, то можно говорить об истинности тождества.
Данные диаграммы являются эффективным методом визуализации операций с множествами. Отдельные множества изображают в виде кругов, а универсальное множество представляют прямоугольником.
Дополнение множества
Объединение множеств
Пересечение множеств
Разность множеств
Симметричная разность множеств
Использование диаграмм Эйлера-Венна для доказательства логических равенств
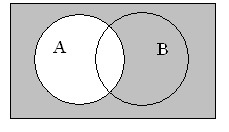
В качестве доказательства логического равенства подходит способ построения диаграмм Эйлера-Венна. Для примера можно представить доказательства следующего выражения: ¬(АvВ) = ¬А&¬В. Равенство демонстрирует запись закона де Моргана. В первую очередь следует наглядно изобразить левую часть уравнения. Для этого необходимо последовательно заштриховать серым цветом все круги, то есть применить дизъюнкцию. Отобразить инверсию можно с помощью закрашивания черным цветом области вне этих кругов.
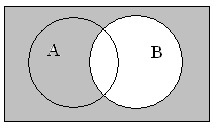
Далее следует визуально представить правую часть выражения. Последовательность действий в этом случае такова: необходимо заштриховать область, в которой отображается инверсия (¬А), с использованием серого цвета и аналогично закрасить область ¬В; отобразить конъюнкцию в виде пересечения этих серых областей. Результат такого наложения будет окрашен черным цветом.
На рисунке видно, что области, в которых отображены левая и правая части уравнения, равны друг другу. Таким образом, закономерность доказана.
Решение задачи поиска информации в Интернет с помощью диаграмм Эйлера-Венна
Изучая тему поиска информации в глобальной сети Интернет, нельзя обойтись без примеров поисковых запросов, в которых использованы логические связки. Как правило, их смысл аналогичен союзам «и», «или» из русского языка. Принцип действия можно понять, если изобразить логические связи с помощью графической схемы или диаграммы Эйлера-Венна.
Как логические операции связаны с теорией множеств
Используя диаграммы Эйлера-Венна, принято наглядно демонстрировать связь логических действий и теории множеств. Операции логики можно задать с помощью таблиц истинности. В этом случае следует руководствоваться общим принципом.
На диаграмме в виде области круга под названием А отображают истинность определения А, то есть теоретически круг А обозначает все элементы, которые включены в данное множество. Таким образом, область за пределами круга А будет обозначать ложь соответствующего утверждения.
Понимание, какая область диаграммы отражает логическую операцию, возникает после того, как будут заштрихованы только те области, в которых значения логической операции на наборах А и В соответствуют истине. К примеру, импликация истинна при (00, 01 и 11).
Необходимо заштриховать сначала область за пределами пары пересекающихся кругов в соответствии со значениями А=0, В=0. Затем закрасить область в круге В, которая относится к значениям А=0, В=1, и область, соответствующую и кругу А, и кругу В, то есть участок пересечения, отображающий значения А=1, В=1. Эти три области в комплексе являются графическим представлением логической импликации.
Примеры задач с решением
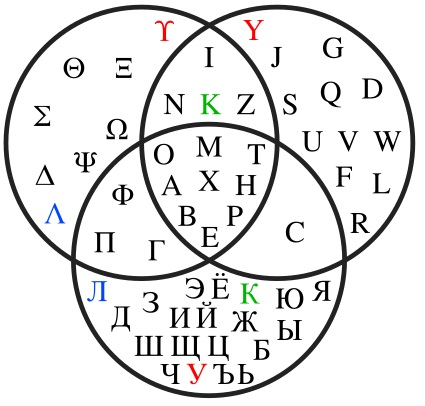
Диаграммы Эйлера-Венна могут содержать три и более круга. Преимуществом данного графического способа представления выражений является его высокая эффективность и наглядность. К примеру, можно изобразить диаграмму пересечений букв из русского, латинского и греческого алфавита:
Понять суть методики удобно на практике. Можно решить несколько задач с применением диаграмм Эйлера-Венна.
Задача 1
По условию есть таблица поисковых запросов. В ней представлены страницы по некоторому сегменту. Требуется определить, сколько страниц в тысячах будет отображаться по запросу «Эсминец». Следует отметить, что запросы выполнялись практически в одно время, поэтому набор страниц с искомыми словами не менялся в процессе выполнения запросов.
Решение
Ф – является числом страниц (в тысячах) в соответствии с запросом «Фрегат»;
Э – является числом страниц (в тысячах) в соответствии с запросом «Эсминец»;
Х – представляет собой число страниц (в тысячах) по запросу, в котором присутствует «Фрегат» и отсутствует «Эсминец»;
У – определяет число страниц (в тысячах) по запросу, в котором указано слово «Эсминец» и отсутствует слово «Фрегат».
Диаграмма для каждого поискового запроса будет иметь следующий вид:
Исходя из информации по диаграммам, получим:
Х+900+У = Ф+У = 2100+У = 3400
У = 3400-2100 = 1300
Э = 900+У = 900+1300= 2200
Ответ: по запросу «Эсминец» будет найдено 2200 страниц
Задача 2
Класс состоит из 36 учеников. Дети ходят на занятия в рамках математического, физического, химического кружка. Факультатив по математике посещают 18 учащихся, по физике – 14, по химии – 10. Также известно, что 2 ученика ходят на все три кружка, 8 – на математику и физику, 5 – на математику и химию, 3 – на физику и химию. Необходимо определить количество учеников, которые не посещают ни одного кружка.
Решение
Решить данную задачу можно с помощью удобного и наглядного метода в виде кругов Эйлера. Наибольшим кругом следует обозначить множество всех учащихся класса. Внутри этой окружности необходимо изобразить пересекающиеся множества в виде учащихся на факультативе по математике (М), физике (Ф), химии (Х).
МФХ – является множеством учеников, каждый из которых ходит на занятия во все три кружка;
МФ¬Х – определяет множество учащихся, которые посещают факультативы по математике и физике, но не ходят на занятия по химии.
¬М¬ФХ – представляет собой множество людей, каждый из которых посещает химический факультатив, но отказался от дополнительных занятий по физике и математике.
По аналогичному принципу можно ввести множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Согласно условиям задачи, пара учеников записаны во все три кружка. Поэтому в область МФХ требуется вписать число 2. Исходя из того, что 8 учащихся посещают факультативы по математике и физике, а из них двое школьников ходят во все кружки, то в области МФ¬Х следует отметить 6 человек (8-2). Аналогичным способом можно определить число учеников в остальных множествах:
Далее требуется определить сумму учеников по всем областям:
Таким образом, всего 28 учащихся посещают факультативные занятия.
Ответ: 8 учеников из класса не посещают ни одного кружка.
Задача 3
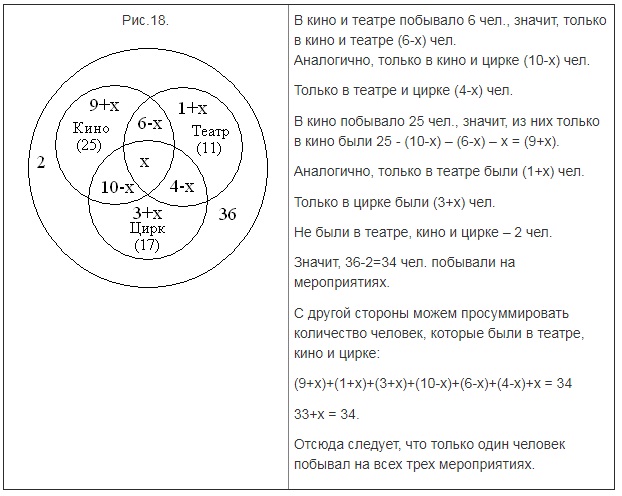
Когда закончились зимние каникулы, преподаватель поинтересовался у учеников, кто из них посещал театр, кино или цирк. Всего в классе 36 человек. По полученной информации, два ребенка не были ни в кино, ни в театре, ни в цирке. Кино посетили 25 школьников, театр – 11, цирк – 17. И в кино, и в театр сходили 6 человек, и в кино, и в цирк – 10, и в театр, и в цирк – 4. Необходимо посчитать, какое количество учащихся из класса посетили и кино, и театр, и цирк.
Решение
Предположим, что х представляет собой число учеников, которые посетили и кино, и театр, и цирк. В таком случае, можно изобразить диаграмму и определить число школьников для каждой области:
Ответ: 1 ученик побывал и в кино, и в театре, и в цирке.
Источник
Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ
В курсе Информатики и ИКТ основной и старшей школы рассматриваются такие важные темы как “Основы логики” и “Поиск информации в Интернет”. При решении определенного типа задач удобно использовать круги Эйлера (диаграммы Эйлера-Венна).
Математическая справка. Диаграммы Эйлера-Венна используются прежде всего в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2 n комбинаций n свойств. Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.
2. Представление логических связок в поисковых запросах
При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок, аналогичным по смыслу союзам “и”, “или” русского языка. Смысл логических связок становится более понятным, если проиллюстрировать их с помощью графической схемы – кругов Эйлера (диаграмм Эйлера-Венна).
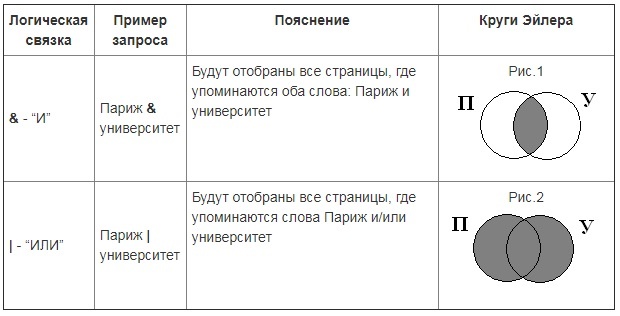
| Логическая связка | Пример запроса | Пояснение | Круги Эйлера |
| & — “И” | Париж & университет | Будут отобраны все страницы, где упоминаются оба слова: Париж и университет | Рис.1 |

3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно наглядно представить связь логических операций с теорией множеств. Для демонстрации можно воспользоваться слайдами в Приложение 1.
Логические операции задаются своими таблицами истинности. В Приложении 2 подробно рассматриваются графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме – область круга с именем А отображает истинность высказывания А (в теории множеств круг А – обозначение всех элементов, входящих в данное множество). Соответственно, область вне круга отображает значение “ложь” соответствующего высказывания. Что бы понять какая область диаграммы будет отображением логической операции нужно заштриховать только те области, в которых значения логической операции на наборах A и B равны “истина”.
Например, значение импликации равно “истина” в трех случаях (00, 01 и 11). Заштрихуем последовательно: 1) область вне двух пересекающихся кругов, которая соответствует значениям А=0, В=0; 2) область, относящуюся только к кругу В (полумесяц), которая соответствует значениям А=0, В=1; 3) область, относящуюся и к кругу А и к кругу В (пересечение) – соответствует значениям А=1, В=1. Объединение этих трех областей и будет графическим представлением логической операции импликации.
4. Использование кругов Эйлера при доказательстве логических равенств (законов)
Для того, чтобы доказать логические равенства можно применить метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(АvВ) = ¬А&¬В (закон де Моргана).
Для наглядного представления левой части равенства выполним последовательно: заштрихуем оба круга (применим дизъюнкцию) серым цветом, затем для отображения инверсии заштрихуем область за пределами кругов черным цветом:
Рис.3 
Для визуального представления правой части равенства выполним последовательно: заштрихуем область для отображения инверсии (¬А) серым цветом и аналогично область ¬В также серым цветом; затем для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения представлен черным цветом):
Рис.5 

Видим, что области для отображения левой и правой части равны. Что и требовалось доказать.
5. Задачи в формате ГИА и ЕГЭ по теме: “Поиск информации в Интернет”
Задача №18 из демо-версии ГИА 2013.
В таблице приведены запросы к поисковому серверу. Для каждого запроса указан его код – соответствующая буква от А до Г. Расположите коды запросов слева направо в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
| Код | Запрос |
| А | (Муха & Денежка) | Самовар |
| Б | Муха & Денежка & Базар & Самовар |
| В | Муха | Денежка | Самовар |
| Г | Муха & Денежка & Самовар |
Для каждого запроса построим диаграмму Эйлера-Венна:

Задача В12 из демо-версии ЕГЭ-2013.
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысяч) |
| Фрегат | Эсминец | 3400 |
| Фрегат & Эсминец | 900 |
| Фрегат | 2100 |
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ф – количество страниц (в тысячах) по запросу Фрегат;
Э – количество страниц (в тысячах) по запросу Эсминец;
Х – количество страниц (в тысячах) по запросу, в котором упоминается Фрегат и не упоминается Эсминец;
У – количество страниц (в тысячах) по запросу, в котором упоминается Эсминец и не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12 |

Согласно диаграммам имеем:
- Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.
- Э = 900+У = 900+1300= 2200.
6. Решение логических содержательных задач методом диаграмм Эйлера-Венна
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14 человек, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек — и математический и физический, 5 и математический и химический, 3 — и физический и химический.
Сколько учеников класса не посещают никаких кружков?
Для решения данной задачи очень удобным и наглядным является использование кругов Эйлера.
Самый большой круг – множество всех учеников класса. Внутри круга три пересекающихся множества: членов математического (М), физического (Ф), химического (Х) кружков.
Пусть МФХ – множество ребят, каждый из которых посещает все три кружка. МФ¬Х – множество ребят, каждый из которых посещает математический и физический кружки и не посещает химический. ¬М¬ФХ — множество ребят, каждый из которых посещает химический кружок и не посещает физический и математический кружки.
Аналогично введем множества: ¬МФХ, М¬ФХ, М¬Ф¬Х, ¬МФ¬Х, ¬М¬Ф¬Х.
Известно, что все три кружка посещают 2 человека, следовательно, в область МФХ впишем число 2. Т.к. 8 человек посещают и математический и физический кружки и среди них уже есть 2 человека, посещающих все три кружка, то в область МФ¬Х впишем 6 человек (8-2). Аналогично определим количество учащихся в остальных множествах:
| Круги Эйлера с названиями непересекающихся множеств: |

Например, количество человек, которые посещают физический кружок 2+6+1+5=14
Просуммируем количество человек по всем областям: 7+6+3+2+4+1+5=28. Следовательно, 28 человек из класса посещают кружки.
Значит, 36-28 = 8 учеников не посещают кружки.
После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино. ни в театре, ни в цирке. В кино побывало 25 человек, в театре — 11, в цирке 17 человек; и в кино, и в театре — 6; и в кино и в цирке — 10; и в театре и в цирке — 4.
Сколько человек побывало и в кино, и в театре, и в цирке?
Пусть х – количество ребят, которые побывали и в кино, и в театре, и в цирке.
Тогда можно построить следующую диаграмму и посчитать количество ребят в каждой области:

Аналогично, только в кино и цирке (10-х) чел.
Только в театре и цирке (4-х) чел.
В кино побывало 25 чел., значит, из них только в кино были 25 — (10-х) – (6-х) – х = (9+х).
Аналогично, только в театре были (1+х) чел.
Только в цирке были (3+х) чел.
Не были в театре, кино и цирке – 2 чел.
Значит, 36-2=34 чел. побывали на мероприятиях.
С другой стороны можем просуммировать количество человек, которые были в театре, кино и цирке:
Отсюда следует, что только один человек побывал на всех трех мероприятиях.
Таким образом, круги Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач.
Источник