Способ задания функции одной переменной

01. Функция одной переменной: способы задания, характеристики поведения. Примеры функциональных зависимостей

Точный математический анализ социально-экономических проблем всегда базируется на понятии функции. Функция — это правило, по которому элементы одного числового множества сопоставляются с элементами другого числового множества. Функции обозначаются как:

, где

х — аргумент функции, объясняющая или независимая переменная, у – значение функции, объясняемая или зависимая переменная.

Существуют четыре способа задания функции: табличный, графический, аналитический, алгоритмический. Некоторые из перечисленных способов задания функций (иногда говорят «функциональных зависимостей») будут рассмотрены ниже на конкретных примерах.

Пример 1: Результаты изучения сезонного спроса на некоторый товар приводятся в таблице.

Для каждого конкретного момента времени в таблице указывается значение спроса на товар в этот момент времени, то есть правило задано таблично.

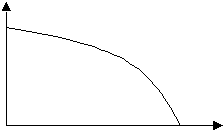
Пример 2: Изучение спроса на некоторый товар в зависимости от изменения цены на него позволило построить следующую графическую зависимость:

Графический способ представления, как очевидно является наиболее удобным с точки зрения очевидности представления данных, но наименее удобным с позиций точности.

Пример 3. Расход продуктов питания Y в зависимости от доходов семьи Х может быть описан следующей зависимостью

Пример 4. Издержки по управлению товарными запасами У Складываются из затрат на хранение и затрат на доставку. В свою очередь каждое слагаемое зависит от объема товарной массы

Где А, b — коэффициенты, характеризующие условия хранения и поставки товара.

Пример 5: В микроэкономике, изучающей поведение потребителя на рынке товаров и услуг, широко используется функция полезности U. Для случая двух товаров, например, чая и кофе, она может иметь вид:

Здесь У1,У2 — объемы потребления каждого вида товара.

Приведённых примеров достаточно, чтобы сделать некоторые выводы.

Во-первых, Аналитические зависимости (формулы) совершенно различны, но все они состоят из конечного числа простых зависимостей, которые называют основными элементарными функциями.

На рис.1 показаны шесть основных элементарных функций (по порядку слева направо):

1. Линейная —

2. Квадратичная

3. Гипербола

4. Логарифмическая

5. Показательная

6. Степенная

Используемые на практике функции состоят из сочетаний нескольких элементарных и строятся по принципу «функция от функции». Например, пусть z = F(y). В свою очередь, переменная У также является функцией, зависящей от х — то есть у = F(x). Тогда говорят, что функция z является сложной функцией вида Z = F(f(x)).

Можно отметить, что функция может зависеть от одной переменной, тогда её можно изобразить на плоскости в виде графика в системе координат. Если аргумента два, как у функции полезности, то она может быть изображена на плоскости в виде совокупности линий уровня (см. рис.2).

Во-вторых, каждый из перечисленных способов задания функции не исключает любой другой. Они лишь дополняют друг друга. В одних задачах удобнее использовать аналитическую зависимость, а в других — графическую.

Кроме этого, можно отметить, что можно производить переход от одного способа представления функций к другому.

В-Третьих, функциональные зависимости полезны не только тем, что позволяют вычислить объясняемую переменную при заданных значениях объясняющих переменных, но и тем, что позволяют выявить качественные особенности описываемого явления.

Например, исследуем как изменяются затраты на продукты питания (см. пример 2), если доход увеличивается на величину Dх. Новое значение затрат определится как

Таким образом очевидно, что увеличение затрат на питание не зависит от дохода Х, а зависит лишь от прироста дохода Dх. Это означает, что, если индивид получал 800 руб. в месяц и его зарплата увеличится на 20 руб., то из этой величины он выделит дополнительно на питание 14 руб. То же самое сделает другой человек при зарплате 1600 руб. в месяц, если его зарплата также увеличится на 20 руб.

Источник

Тема 1. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ

1.1. Определение функции одной переменной

Определение. Пусть даны два множества X и Y. Если каждому элементу x из множества X по некоторому правилу f соответствует единственный элемент y из множества Y, то говорят, что на множестве X определена функция y = f ( x ) с областью определения X = D( f ) и областью изменения Y = E ( f ). При этом x считают независимой переменной, или аргументом функции, а y – зависимой переменной или функцией.

Частным значением функции y = f ( x ) при фиксированном значении аргумента x = x₀ называют y ₀ = f ( x ₀ ).

Графиком функции y = f ( x ) называют геометрическое место точек M ( x ; f ( x )) на плоскости Oxy , где x Î D ( f ) и f ( x ) Î E ( f ).

1.2. Способы задания функции

1) Аналитический способ – способ задания функции с помощью формулы.

Различают несколько способов аналитического задания функции:

а) Функция задана явно формулой y = f ( x ).

Например: 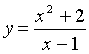, где D( y ) = (– ∞;1) (1;+∞).

б) Функция задана неявно уравнением, связывающем x и y : F( x ; y ) = 0.

Например: – уравнение окружности с центром в начале координат и радиусом r . Если из этого уравнения выразить y через x , то получится две функции:

и ,

которые имеют область определения , а области значений этих функций будут: для первой – , для второй – .

в) Функция задана параметрически с помощью некоторого параметра t , причём и аргумент x , и функция y зависят от этого параметра:

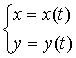
Например: можно задать окружность с помощью параметрических уравнений:

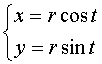
2) Табличный способ задания функции – например, таблицы Брадиса задают функции y = sin x , y = cos x и др.

3) Графический способ задания функции, когда зависимость функции от её аргумента задаётся графически.

1.3. Сложная и обратная функции

Определение 1 . Пусть функция y = f ( U) определена на множестве D( f ), а функция U = g ( x ) определена на D( g ), причём E( g ) D( f ).

Тогда функция y = F( x ) = f ( g ( x )) называется сложной функцией (или функцией от функции, или суперпозицией функций f и g ) .

Определение 2 . Пусть задана функция y = f ( x ) взаимно однозначно отображающая множество X = D ( f ) на множество Y = E ( f ). Тогда функция x = g ( y ) называется обратной к функции y = f ( x ), т. е. любому y E( f ) соответствует единственное значение x D ( f ), при котором верно равенство y = f ( x ).

Замечание. Графики функций y = f ( x ) и x = g ( y ) представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить x , а зависимую y , то графики функций y = f ( x ) и y = g ( x ) будут симметричны относительно биссектрисы первого и третьего координатных углов.

1.4. Элементарные функции

Основные элементарные функции:

y = const ( постоянная функция), D ( y ) = R ; E ( y ) = c .

( линейная функция), D ( y ) = R ; E ( y ) = R .

y = ( степенная функция), α Î R , E( y ), D ( y ) зависят от α .

y = ( показательная функция), a > 0, a ≠ 1, D ( y ) = R , E ( y ) = ( 0; +∞).

y = ( логарифмическая функция) ), a > 0, a ≠ 1, D ( y ) = (0;+∞), E ( y ) = R .

y = sin x , D ( y ) = R , E ( y ) = .

y = cos x, D( y) = R, E( y) = .

y = tg x, D( y) = , E( y) = R.

y = ctg x, D( y) = , E( y) = R.

Обратные тригонометрические функции :

y = arcsin x , D ( y ) = , E ( y ) = .

y = arccos x, D( y) = , E( y) = .

y = arctg x , D ( y ) = R , E ( y ) = .

y = arcctg x , D ( y ) = R , E ( y ) = .

Элементарной функцией называется функция, составленная из основных элементарных функций с помощью конечного числа операций сложения, вычитания, умножения, деления и суперпозиции.

Например: – элементарная функция.

Графики обратных тригонометрических функций:

Источник