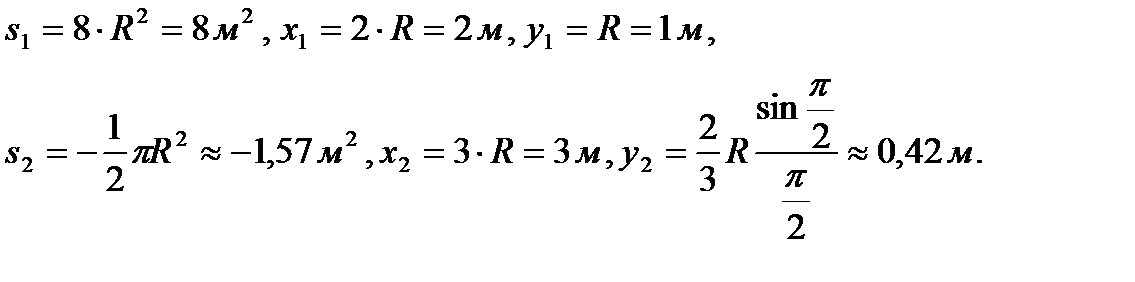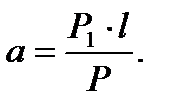Способ взвешивания определения центра тяжести

Методы нахождения центров тяжести тел

Из соображений симметрии.

Если тело имеет центр материальной симметрии, то его центр тяжести совпадает с этим центром симметрии. Отсюда, например, следует, что центр тяжести однородного шара совпадает с центром шара (см. рис. 116).

Если тело имеет ось материальной симметрии, то его центр тяжести лежит на оси симметрии. Исходя из этого, легко найти центр тяжести однородной прямоугольной пластинки (см. рис. 117).

Если тело имеет плоскость материальной симметрии, то его центр тяжести лежит в плоскости симметрии. Пользуясь этим, легко найти центр тяжести однородного кругового цилиндра (см. рис. 118).

Метод разбиения тела на части.

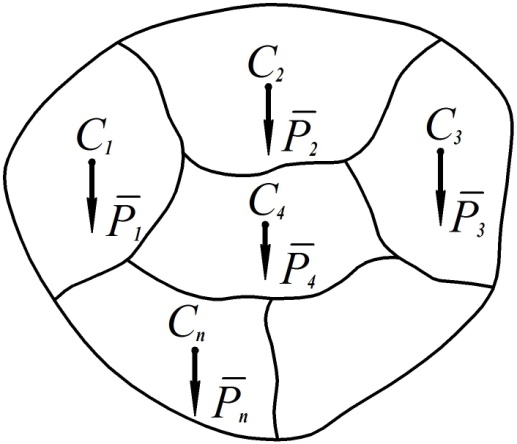
Пусть тело можно разбить на несколько частей, для каждой из которых положение центра тяжести известно (см. рис. 119). Тогда общий центр тяжести тела может быть найден по формуле

(86)

Метод отрицательных масс.

Этот метод является обобщением метода разбиения тела на части на случай, когда тело имеет пустые полости с известным положением их центров тяжести, если эти полости заполнить веществом. В этом случае можно считать тело с пустыми полостями состоящим из воображаемого тела с заполненными полостями и телами в виде полостей, которым следует приписать отрицательную массу. После этого центр тяжести исходного тела можно найти по формуле (86). Поясним этот метод на примере.

Пример 10

Определим положение центра тяжести однородной прямоугольной пластинки с вырезанным полукругом ( см. рис. 120 ). Пусть задан радиус

вырезанного полукруга R=1 м. Выберем оси координат, как показано на рисунке. Эту пластинку можно рассматривать как фигуру, составленную из прямоугольной пластинки и полукруга с отрицательной массой. Площади таких фигур и координаты их центров тяжести равны:

Далее в соответствии с формулой (86) найдем координаты центра тяжести пластинки:

Это экспериментальный метод, с помощью которого удобно находить положение центров тяжести плоских, в том числе и неоднородных, тел. Тело, подвешенное на нити, находится в равновесии под действием двух сил: силы тяжести, приложенной в центре тяжести, и силы натяжения, направленной вдоль нити. Эти две силы равны по величине и направлены вдоль одной прямой, являющейся продолжением нити. Поэтому для нахождения центра тяжести достаточно два раза подвесить тело за две различные точки и в условиях равновесия отметить на теле продолжение нити (см. рис. 121).

В результате центр тяжести найдем как точку пересечения двух полученных прямых.

Этот экспериментальный метод используют для нахождения центров тяжести транспортных средств. Для его реализации используются весы, приспособленные для взвешивания транспортных средств. Для нахождения центра тяжести снимают два показания весов: Р – для случая, когда транспортное средство опирается на платформу весов четырьмя колесами, и — для случая, когда транспортное средство опирается на платформу весов двумя колесами (см. рис. 122).

В результате первого взвешивания определяется вес транспортного средства Р. Результат второго взвешивания дает силу давления передних колес на платформу весов при втором взвешивании.

Рассмотрим теперь в качестве объекта равновесия транспортное средство при втором взвешивании. Оно находится в равновесии под действием трех сил 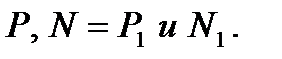Обозначим — колесную базу транспортного средства и — расстояние по горизонтали от центра тяжести до оси задних колес (см. рис. 122). Для такой системы сил сумма алгебраических моментов относительно точки касания задними колесами опорной поверхности равна нулю:

Отсюда, учитывая, что , найдем

Библиографический список

1. Тарг, С.М. Краткий курс теоретической механики/ С.М. Тарг. М.: Высшая школа, 2007. 416с.

2. Яблонский, А.А. Курс теоретической механики/ Яблонский, А.А., Никифорова, В.М. СПб.: Лань, 2001. 764 с.

3. Мещерский, И.В. Сборник задач по теоретической механике/ И.В. Мещерский.: Лань, 2001. 448с.

4. Сборник заданий для курсовых работ по теоретической механике/ Под ред. А.А. Яблонского. М.: Интеграл-Пресс, 2001. 382с.

5. Сборник коротких задач по теоретической механике/ Под ред. О.Э. Кепе. СПб.: Лань, 2008. 368с.

О Г Л А В Л Е Н И Е

Раздел 1. КИНЕМАТИКА 4

Глава 1. КИНЕМАТИКА ТОЧКИ 4

1.1. Векторный способ задания движения точки 4

1.2. Задание движения точки в декартовых координатах 6

1.3.Задание движения точки естественным способом 8

Глава 2. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 14

2.1. Поступательное движение твердого тела 14

2.2. Вращательное движение твердого тела 16

2.2.1. Основные понятия 16

2.2.2. Угловая скорость и угловое ускорение тела 17

2.2.3. Простейшие случаи вращательного движения твердого тела 18

2.2.4. Определение скоростей и ускорений точек тела 19

2.2.5. Векторные формулы для скоростей и ускорений точек тела 20

Глава 3. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ 23

3.1. Основные понятия 23

3.2. Связь между полной и локальной производными от вектора 25

3.3. Теорема сложения скоростей при сложном движении точки 27

3.4. Теорема сложения ускорений при сложном движении точки 30

Глава 4. ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА 37 4.1. Основные понятия 37

4.2. Скорости точек тела при плоском движении 40

4.3. Мгновенный центр скоростей 42

4.4. Ускорения точек тела при плоском движении 47

4.5. Мгновенный центр ускорений 48

4.6. Вычисление угловой скорости и углового ускорения тела при

плоском движении 52

Раздел 2. СТАТИКА 54

Глава 1. ВВЕДЕНИЕ В СТАТИКУ 54

1.1.Основные понятия 54

1.2. Аксиомы статики 56

1.3. Основные виды связей и их реакции 58

Глава 2. СИСТЕМА СХОДЯЩИХСЯ СИЛ 62

2.1. Классификация систем сил 62

2.2. Приведение сходящейся системы сил к равнодействующей 62

2.3. Уравнения равновесия 63

Глава 3. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ 66

3.1. Векторный момент силы относительно точки 66

3.2. Момент силы относительно оси 67

3.3. Алгебраический момент силы относительно точки 70

Глава 4. ПАРА СИЛ И ЕЕ СВОЙСТВА 71

4.1. Понятие о паре сил 71

4.2. Основные свойства пар сил 72

Глава 5. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ 74

5.1. Приведение произвольной пространственной системы сил к центру 74

5.2. Частные случаи приведения системы сил к центру 76

Глава 6. УРАВНЕНИЯ РАВНОВЕСИЯ 79

6.1. Независимые уравнения равновесия для различных систем сил 79

6.2. Различные формы независимых уравнений равновесия для плоской произвольной системы сил 81

6.3. Непрерывно распределенная нагрузка 85

6.4. Равновесие системы тел 88

Глава 7. ТРЕНИЕ И ФЕРМЫ 93

7.1. Трение скольжения 93 7.2. Трение качения 95 7.3. Расчет ферм 97

Глава 8. ЦЕНТР ТЯЖЕСТИ 103

8.1. Основные понятия 103 8.2. Центры тяжести простейших однородных тел 106 8.3. Методы нахождения центров тяжести тел 108

Библиографический список 112

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

Техническая механика

Методы нахождения центра тяжести

Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:

• метод симметрии;
• метод разбиения;
• метод отрицательных масс.

Рассмотрим приемы, применяемые в каждом из перечисленных методов.

Метод симметрии

Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1) .

В этом случае каждой элементарной частице силой тяжести G_i с абсциссой y_i = +a соответствует такая же элементарная частица с абсциссой y_i = -a , тогда:

Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.

Аналогично можно доказать и следующие положения:

• Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
• Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
• Центр тяжести однородного тела вращения лежит на оси вращения.

Метод разбиения

Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.

Допустим, что мы разбили тело силой тяжести G на три части G’ , G» , G»’ , абсциссы центров тяжести этих частей x’_C, x»_C, x»’_C известны.
Формула для определения абсциссы центра тяжести всего тела:

Перепишем ее в следующем виде:

Последнее равенство запишем для каждой из трех частей тела отдельно:

Сложив левые и правые части этих трех равенств, получим:

Но правая часть последнего равенства представляет собой произведение Gx_C , так как

Следовательно, x_C = (G’x’_C + G»x»_C + G»’x»’_C)/G , что и требовалось доказать.
Аналогично определяются координаты центра тяжести на координатных осях y и z :

Полученные формулы аналогичны формулам для определения координат цента тяжести, выведенные выше. Поэтому в исходные формулы можно подставлять не силы тяжести элементарных частиц G_i , а силы тяжести конечных частей; под координатами x_i , y_i , z_i понимают координаты центров тяжести частей, на которые разбито тело.

Метод отрицательных масс

Этот метод заключается в том, что тело, имеющее свободные полости, считают сплошным, а массу свободных полостей – отрицательной. Вид формул для определения координат центра тяжести тела при этом не меняется.

Таким образом, при определении центра тяжести тела, имеющего свободные полости, следует применять метод разбиения, но считать массу полостей отрицательной.

Практические методы определения центра тяжести тел

На практике для определения центра тяжести плоских тел сложной формы часто применяют метод подвешивания , который заключается в том, что плоское тело подвешивают на нити за какую-нибудь точку. Прочерчивают вдоль нити линию, и тело подвешивают за другую точку, не находящуюся на полученной линии.
Затем вновь проводят линию вдоль нити.
Точка пересечения двух линий и будет являться центром тяжести плоского тела.

Еще один способ определения центра тяжести, применяемый на практике, называется метод взвешивания . Этот метод часто применяется для определения центра тяжести крупных машин и изделий – автомобилей, самолетов, колесных тракторов и т. п., которые имеют сложную объемную форму и точечную опору на грунт.
Метод заключается в применении условий равновесия, исходя из того, что сумма моментов всех сил, действующих на неподвижное тело равна нулю.
Практически это осуществляется взвешиванием одной из опор машины (задние или передние колеса устанавливаются на весы), при этом показания весов, по сути, являются реакцией опоры, которая учитывается при составлении уравнения равновесия относительно второй точки опоры (находящейся вне весов).
По известной массе (соответственно – весу) тела, показанию весов в одной из точек опоры, и расстоянию между точками опоры можно определить расстояние от одной из точек опоры до плоскости, в которой расположен центр тяжести.
Чтобы найти подобным образом линию (ось), на которой расположен центр тяжести машины, необходимо произвести два взвешивания по принципу, изложенному выше для метода подвешивания (см. рис. 1а) .

Положение центра тяжести некоторых фигур

Прямоугольник. Так как прямоугольник имеет две оси симметрии, то центр тяжести его площади находится в точке пересечения этих осей, иначе говоря, в точке пересечения диагоналей прямоугольника.

Треугольник. Пусть дан треугольник АBD (см. рисунок 2) .
Разобьем его на элементарные (бесконечно узкие) полоски, параллельные стороне AD . Центр тяжести каждой полоски будет лежать на медиане Bd (т. е. в середине каждой полоски) , следовательно, на этой медиане будет лежать и центр тяжести всей площади треугольника. Разбив треугольник на элементарные полоски, параллельные стороне AB , увидим, что искомый центр тяжести лежит и на медиане aD .
Проделав аналогичное действие с треугольником относительно стороны ВD , получим тот же результат – центр тяжести находится на соответствующей медиане.
Следовательно, центр тяжести всей площади треугольника лежит на точке пересечения его медиан, поскольку эта точка является единственной общей точкой для всех трех медиан данной геометрической фигуры.

Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в соотношении 1:2 от основания. Следовательно, центр тяжести треугольника расположен на расстоянии одной трети высоты от каждого основания.

Дуга окружности. Возьмем дугу окружности АВ радиусом R с центральным углом 2α (см. рисунок 3) . Систему координат выберем так, чтобы начало координат было в центре окружности, а ось x делила дугу пополам, тогда y_C = 0 вследствие симметрии дуги относительно оси x . Определим координату центра тяжести x_C .

Разобьем дугу АВ на элементарные части l_i , одна из которых изображена на рисунке. Тогда, согласно сделанным выше выводам,

Дугу l_i вследствие малости примем за отрезок прямой. Из подобия треугольника OD_iC_i и элементарного треугольника S (на рисунке заштрихован) получим:

поскольку RΣΔy_i = AB , а Σl_i = l – длина дуги АВ . Но АВ = 2R sinα , а l = 2Rα , следовательно,

При α = π/2 рад (полуокружность) , x_C = 2R/π .

Круговой сектор. Возьмем сектор радиусом R с центральным углом 2α (см. рисунок 3а) . Проведем оси координат, как показано на рисунке (ось x направлена вдоль оси симметрии сектора), тогда y_C = 0 .

Определим x_C , для чего разобьем сектор на ряд элементарных секторов, каждый из которых из-за малости дуги l_i можно принять за равнобедренный треугольник с высотой R . Тогда центр тяжести каждого элементарного сектора будет находиться на дуге радиуса 2R/3 и задача определения центра тяжести сектора сводится к определению центра тяжести этой дуги.
Очевидно, что

При α = π/2 рад (полукруг) : x_C = 4R/(3π) .

Пример решения задачи на определение центра тяжести

Задача:
Определить положение центра тяжести сечения, составленного из двутавра № 22 и швеллера № 20, как показано на рисунке 4 .

Решение.
Из курса инженерной графики известно, что номер проката соответствует наибольшему габаритному размеру его сечения, выраженного в сантиметрах.

Так как сечение, составленное из двутавра и швеллера, представляет собой фигуру, симметричную относительно оси y , то центр тяжести такого сечения лежит на этой оси, т. е. x_C = 0 .
По справочнику определим площади и координаты центров тяжести двутавра 1 и швеллера 2.

Для двутаврового сечения: А₁ = 15,2 см 2 ; y₁ = 22/2 = 11 см.
Для швеллерного сечения: А₂ = 12 см 2 ; y₂ = 22 + d – z₀ = 22 + 0,32 – 1,25 = 21,07 см ,
где d – толщина стенки швеллера; z₀ – размер, определяющий положение центра тяжести швеллера.

Применим формулу для определения координаты центра тяжести всего сечения:

Источник