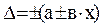Способ выражения пределов допускаемой погрешности

Приложение 3 (справочное). Формы выражения и способы установления пределов допускаемых погрешностей средств измерений

Формы выражения и способы установления пределов допускаемых погрешностей средств измерений

1. Формы выражения пределов допускаемых погрешностей

1.1. Пределы допускаемых погрешностей выражают в зависимости от характера изменения (в пределах диапазона изменений входного (выходного) сигнала) границ абсолютных погрешностей средств измерений конкретного вида, которые оценивают на основании принципа действия, свойств средств измерений, а также их назначения:

в форме приведенных погрешностей — если указанные границы можно полагать практически неизменными. Например пределы допускаемых погрешностей показывающих амперметров выражают в форме приведенных погрешностей, так как границы погрешностей средств измерений данного вида практически неизменны в пределах диапазона измерений;

в форме относительных погрешностей — если указанные границы нельзя полагать постоянными.

1.2. Пределы допускаемых погрешностей выражают в форме абсолютных погрешностей (т.е. в единицах измеряемой величины или в делениях шкалы средств измерений), если погрешность результатов измерений в данной области измерений принято выражать в единицах измеряемой величины или в делениях шкалы. Например пределы допускаемых погрешностей мер массы (длины) выражают в форме абсолютных погрешностей, так как погрешности результатов измерений массы (длины) принято выражать в единицах массы (длины).

2. Способы установления пределов допускаемых погрешностей

2.1. Пределы допускаемых погрешностей, выраженные в форме абсолютных (относительных) погрешностей, устанавливают одним из следующих способов в зависимости от характера изменения (в пределах диапазона измерений входного (выходного) сигнала) границ погрешностей средств измерений конкретного вида:

по формуле (1) настоящего стандарта — если границы абсолютных погрешностей можно полагать практически неизменными;

по формуле (4) настоящего стандарта — если границы относительных погрешностей можно полагать практически неизменными;

по формуле (2) или (5) настоящего стандарта — если границы абсолютных погрешностей можно полагать изменяющимися практически линейно;

в виде функции, графика или таблицы — если границы погрешностей необходимо принять изменяющимися нелинейно.

Откройте актуальную версию документа прямо сейчас или получите полный доступ к системе ГАРАНТ на 3 дня бесплатно!

Если вы являетесь пользователем интернет-версии системы ГАРАНТ, вы можете открыть этот документ прямо сейчас или запросить по Горячей линии в системе.

Источник

Способы выражения и нормирования пределов погрешностей.

Погрешности устанавливаются в виде: абсолютной; относительной; приведённой; в виде числа деления шкалы.

Абсолютная погрешность – это разность между результатом измерения и истинным значением измеряемой величины.

Предел допустимой абсолютной погрешности выражается:

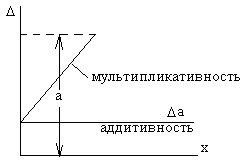
D=±(a+bx) – линейная зависимость, где a и b const.

Нормирование по абсолютной погрешности имеет недостаток в том, что нельзя сравнивать по точности приборы различного назначения.

Относительная погрешность – это отношение абсолютной погрешности к значению измерительной величины

d=D/х*100% Имеет знак зависящий от знака абсолютной погрешности.

Предел относительной погрешности в процентах выражается:

А) d=±C, где С в процентах не мультипликативная погрешность.

Б) d=±[C+d(x_k/x-1)], где c и d постоянные числа (когда есть мультипликативная погрешность)

x_k – конечное значение диапазона измерения. В этой форме x_k и x берутся без учёта знаков.

Недостатки относительной погрешности: при x®0 d®¥ и сравнения становятся бессмысленными.

Приведённые погрешности – отношение абсолютной погрешности к нормировочному значению

Нормирующее значение – условно принятое значение, зависящее от вида шкалы прибора. Для СИ у которых нулевая метка находится на краю или вне шкалы нормирующее значение выбирается равным конечному значению диапазона измерений.

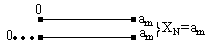
Дли СИ, у которых нулевая отметка находится внутри диапазона измерения – нормирующее значение равно арифметической сумме конечных значений диапазона.

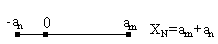
Для СИ предназначенных для измерения номинальных значений X_N равно этому номинальному значению .

Обобщённой метрологической хар-кой СИ является класс точности, который определяет допускаемые пределы всех погрешностей, а также все другие свойства влияющие на точность СИ.

Для СИ, пределы допускаемых погрешностей, которые выражаются в виде относительных или приведённых погрешностей, установлен ряд чисел для выражения пределов допускаемых погрешностей и применяемых для обозначения классов точностей.

(1, 1.5, 2, 2.5, 4, 5, 6)10 n , где n=1, 0, -1, -2, -3, …

Для СИ у которых основную погрешность нормируют в виде предела приведённой погрешности, класс точности численно равен этому пределу.

Если предел допускаемой основной погрешности определяется по двучленной формуле, то в обозначении класса точности вводятся оба числа c и d через косую черту.

Пример задачи на экзамене.

Вольтметр, класс точности 0,5. С какой точностью измерено 100 вольт?

V=100,0±1,5 в 0.5=D/300*100

Правильность результата: погрешность не более 2-х значимых цифр. Последний разряд погрешности и последний разряд результата должны соответствовать друг другу.

Источник

Способ выражения пределов допускаемой погрешности

СПОСОБЫ ВЫРАЖЕНИЯ ПРЕДЕЛОВ ДОПУСКАЕМОЙ ПОГРЕШНОСТИ.

В соответствии с ГОСТОМ пределы допускаемой основной и дополнительной погрешности средств измерений могут устанавливаться в виде абсолютных, относительных, приведенных погрешностей, либо в виде числа делений шкалы. Абсолютная погрешность выражается в тех же единицах, что и измеряемая величина. Пределы допустимой погрешности выражаются:

1) одним числом Δ =±а ,

2) линейной зависимостью Δ=±( а+bx ), a,b – const , x – значение измеряемой величины. В виде таблицы пределов погрешностей для разных номинальных значений показаний измерений.

Относительная погрешность – это отношение абсолютной погрешности к значению измеряемой величины. Предел относительной погрешности выражен в %, одной из следующих формул:

2) ⎥⎦⎤⎢⎣⎡ −+±=1хxdс k δ ; c,d – const , x – значение измеряемой величины в диапазоне измерений.

3) приведенная погрешность – отношение абсолютной погрешности к нормирующему значению % 100 ⋅ Δ= n хδ . Нормирующее значение принимается равным – для средств измерений с равномерной или степенной шкалой, если нулевая отметка на краю или вне шкалы – конечному значению диапазона измерений. Если нулевая отметка находится, сумме конечных значений диапазона измерений. Обобщенной метрологической характеристикой средств измерения является класс точности, который определяет допускаемые пределы всех погрешностей, а также все другие свойства, влияющие на точность средств измерения. Для средств измерения, пределы допускаемых погрешностей для которых выражены в виде относительных или приведенных погрешностей, а также все другие свойства, влияющие на точность средств измерения. Для средств измерения, пределы допускаемых погрешностей которых выражены в виде относительных или приведенных погрешностей ГОСТОМ установлен следующий ряд чисел для выражения предела допускаемой погрешности и применяют для обозначения класса точности , , , , , , где n=1,0,-1,-2…

Источник

Способы выражения пределов допускаемых погрешностей средств измерений.

Пределом допускаемой погрешности средств измерений называется наибольшее (без учёта знака) его погрешность , при которой это средство может быть признано годным.
Например вольтметр годности 0 (инструментальная погрешность от 0 до +/- 1 %)

Вопросы нормирования погрешности рассматривает ГОСТ 8.401-80 «КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЯ. ОБЩИЕ ТРЕБОВАНИЯ». Согласно этого ГОСТа пределы, допускаемые основной и дополнительной погрешностями, выражаются в форме приведённых абсолютных или относительных погрешностях. Форма представления пределов допускаемой погрешности выбирается отноосительно характера измерения погрешности в пределах диапазона измерений. Пределы допускаемой абсолютной погрешности (∆Х=±а).

Если присутствует аддетивная погрешность, то в эту формулу вводят слагаемое (bx).

Пределы допускаемой приведённой основной погрешности (γ= *100%=±р), где ∆ х – предел допускаемой абсолютной погрешности, N –нормирующее значение. Нормирующее значение выбирается следующим образом: для средств измерения с равномерной или степенной шкалой, и если нулевое значение входного сигнала находится на краю или вне диапазона измерений, то нормирующее значение устанавливает равному большому пределу измерений. Степенная шкала с расширяющимися или сужающимися делениями то Хn выбирается таким же образом. Если имеется шкала с условно принятым нулём (например шкала Цельсия) то нормирующий множитель устанавливают равным модулю разности пределов измерений.

Для измерительных приборов с существенной неравномерной шкалой (например ОММЕТР) нормирующее значение устанавливают равным всей длине шкалы.

Класс точности средств измерения — обобщённая характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерения, влияющими на точность. Класс точности характеризует свойства средств измерений, в отношении точности, но не является непосредственным показателем точности средств измерения, выполняемых с помощью этого средства измерения.
1) Если класс точности установлен по пределу допускаемой относительной погрешности, то на шкале цифра будет находиться в кружочке.
2)Если погрешность прибора признана аддетивной, и прибор нормируется по пределу допускаемой приведённой основной погрешности, то класс точности указывается без кружочков. 3) Если шкала прибора сильно неравномерна, нормирующее значение принято равным длине шкалы, то класс точности обозначается числом в галочке.
Для всех рассмотренных случаев, вместе с условием обозначения класса точности, на шкале, щитке или корпусе измерительного прибора, указывается номер стандарта или ТУ которые устанавливает нормы для средства измерения.

Погрешности измерений.

Погрешность результата измерения – отклонение результата измерения от истинного значения.
Погрешность результата измерения выражается числом, указывающим на возможные границы неопределённости значения измеряемой величины.
По способу такта погрешность результата измерения классифицируется:
— по способу числового выражения (абсолютная, относительная);
— в зависимости от источника возникновения (инструментальные, методические, отсчитывания, установки);
— по закономерностям проявления (систематические, прогрессирующие, случайные, грубые).

Источник

Формы выражения пределов допускаемых погрешностей

• Пределы допускаемой абсолютной погрешности могут быть постоянны

(1)

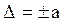
или зависеть от измеряемой величины

, (2)

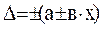
где: 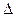— предел допускаемой абсолютной погрешности, выражаемой в единицах на входе (выходе) СИ;

а, в – положительные числа, не зависящие от х;

х – значение измеряемой величины;

Нормирование в соответствии с (2) означает, что в составе погрешности средства измерений присутствует две составляющие погрешности, например, для генератора низкой частоты Г3-36

• Пределы допускаемой относительной погрешности:

если Δ устанавливается по формуле (1),

(3)

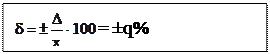
если Δ устанавливается по формуле (2)

, (4)

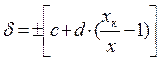
где 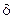— предел допускаемой относительной погрешности, %;

с,d –положительные числа, выбираемые из стандартизованного ряда (1;1.5; 2; 2.5; 3; 4; 5; 6) 10 n , где n=(1.0; 0; -1; -2; и т.д.);

х_к – больший по модулю из пределов измерений;

x – показания прибора.

• Пределы допускаемой приведенной погрешности определяют по формуле:

где — предел допускаемой приведенной погрешности, %;

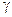
х_N – нормирующее значение, равное большему из модулей пределов измерения;

Нормирующее значение для СИ с равномерной, практически равномерной или степенной шкалой, а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находятся на краю или вне диапазона измерений, следует устанавливать равным большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений.

Для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений нормирующее значение допускается устанавливать равным сумме модулей пределов измерений.

Для СИ ФВ, для которых принята шкала с условным нулем, нормирующее значение устанавливают равным модулю разности пределов измерений. Для милливольтметра термоэлектрического термометра с пределами измерений 200 и 600 0 С нормирующее значение равно 400 0 С.

Для СИ с установленным номинальным значением нормирующее значение устанавливают равным этому номинальному значению. Для частотомеров с диапазоном измерения 45-55 Гц и номинальной частотой 50 Гц нормирующее значение равно 50 Гц.

q –положительное число, выбираемое из стандартизованного ряда (1;1.5; 1,6; 2; 2.5; 3; 4; 5; 6) 10 n , где n=(1.0; 0; -1; -2; и т.д.);

Пределы допускаемых дополнительных погрешностей устанавливают:

1. В виде постоянного значения дл всей рабочей области влияющей величины или в виде постоянных значений по интервалам рабочей области влияющей величины;

2. Путем указания отношения предела допускаемой дополнительной погрешности, соответствующую регламентированному интервалу влияющей величины, к этому интервалу;

3. Путем указания зависимости предела допускаемой дополнительной погрешности от влияющей величины (предельной функции влияния);

4. Путем указания функциональной зависимости пределов допускаемых отклонений от номинального значения функции.

Пределы допускаемых дополнительных погрешностей устанавливают:

в виде дольного значения предела допускаемой основной погрешности.

Обозначение классов точности средств измерений

1. Для средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме абсолютных или относительных погрешностей, причем последние установлены в виде графика, таблицы или формулы,не в соответствии с выражениями (1,2,3,4 ), классы точности следует обозначать в документации прописными буквами латинского алфавита (например, М, С) или римскими цифрами (I, II).

2. Для измерительных приборов пределы допускаемой погрешности которых выражены как приведенные погрешности согласно выражению (5), или относительной погрешности, согласно (3) классы точности обозначаются числами, равными этим пределам в процентах. Чтобы отличить относительную погрешность от приведенной, обозначение класса точности измерительного прибора для которого пределы допускаемой погрешности выражены в виде относительной погрешности, согласно (3), обводят кружком.

3. Для измерительных приборов, предел допускаемых погрешностей которых выражается относительной погрешностью в процентах, согласно выражению (4) класс точности определяется совокупностью значений с и d, разделяя их косой чертой.

Нанесение обозначения класса точности осуществляется на циферблаты (шкалы), щитки и корпуса приборов.

Таким образом, для большинства применяемых в практике приборов используются одночленные или двучленные обозначения класса точности. Например, обозначение класса точности 0,5 показывает, что пределы допускаемых погрешностей выражаются в процентах нормирующего значения согласно выражению (5). Обозначение класса точности 0.02/0.01 означает что предел допускаемой относительной погрешности в процентах значения измеряемой величины и определяется формулой

, где с=0,02 d=0,01

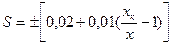
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник