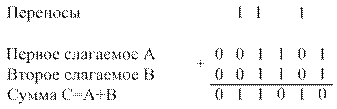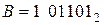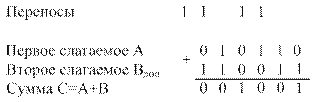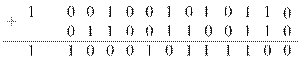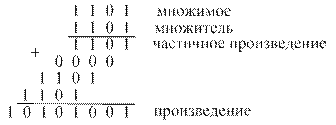Способ выполнения арифметических операций

» Машины должны работать.

Люди должны думать»

сайт Егоровой Марины Евгеньевны

Арифметические операции в двоичной системе счисления

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.

Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.

Пример 1. Сложить двоичные числа

111 + 101, 10101 + 1111:

Пример 2 . Вычесть двоичные числа

10001 — 101 и 11011 — 1101:

Пример 3. Умножить двоичные числа

110 • 11, 111 • 101:

Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.

Арифметические операции в восьмеричной системе счисления

Для представления чисел в восьмеричной системе счисления используются восемь цифр (0, 1, 2, 3, 4, 5, 6, 7), так как основа восьмеричной системы счисления равна 8. Все операции производятся посредством этих восьми цифр. Операции сложения и умножения в восьмеричной системе счисления производятся с помощью следующих таблиц:

Таблицы сложения и умножения в восьмеричной системе счисления

Пример 4. Сложить восьмеричные числа 453 + 671 и 142,63 + 106,71

Пример 5 . Вычесть восьмеричные числа 5153 — 1671 и 2426,63 — 1706,71

Пример 6. Умножить восьмеричные числа 51 • 16 и 16,6 • 3,2

Арифметические операции в шестнадцатеричной системе счисления

Для представления чисел в шестнадцатеричной системе счисления используются шестнадцать цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. В шестнадцатеричной системе число шестнадцать пишется как 10. Выполнение арифметических операций в шестнадцатеричной системе производится как и в десятиричной системе, но при выполнении арифметических операций над большими числами необходимо использовать таблицы сложения и умножения чисел в шестнадцатеричной системе счисления.

Таблица сложения в шестнадцатеричной системе счисления

Таблица умножения в шестнадцатеричной системе счисления

Пример 7. Сложить шестнадцатеричные числа

4A3 + 67C и 14D,F3 + 1A6,79

Пример 8. Вычесть шестнадцатеричные числа

51С — 1А7 и A4,6 — 1C,D

Пример 9. Умножить шестнадцатеричные числа

A1 • 1C и 1,F • 3,A

При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему счисления.

Источник

Порядок действий в математике

О чем эта статья:

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше ( )
меньше (

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

действия выполняются по порядку слева направо
сначала выполняется умножение и деление, а затем — сложение и вычитание.

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо.

Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11- 2 + 5.

В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.

Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.

Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:

8 — 2 * 3 = 8 — 6 = 2.

Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.

Подставляем полученные значения в исходное выражение:

10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.

Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.

И, как всегда, рассмотрим, как это работает на примере.

Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.

В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.

Подставляем полученное значение в исходное выражение:

(4 + 1) * 3 + 36 : 3 — 7.

Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:

(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.

Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.

У нас есть статья «знаки больше, меньше или равно», она может быть полезной для тебя!

Источник

Выполнение арифметических операций

Основной операцией, которая используется в цифровых устройствах при различных вычислениях, является операция алгебраического сложения чисел (сложения в котором могут участвовать как положительные, так и отрицательные числа). Такие операции как умножение и деление также выполняются с помощью операции сложения и некоторых логических операций (например, сдвига результата сложения). Поэтому с операции сложения начнем рассмотрение выполнения арифметических операций микропроцессором.

Сложение положительных двоичных чисел. Выполнение этой операции покажем на примере:

Цифры разрядов суммы формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы получается суммированием цифр младших разрядов слагаемых. При этом, кроме цифры разряда суммы формируется цифра переноса в следующий более старший разряд. Таким образом, в разрядах, начиная со второго, суммируются три цифры: цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего.

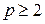
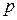
Перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде равен или больше (основание системы счисления). При этом в разряд суммы записывается цифра на единиц (т.е. на 2 единицы) меньшая результата сложения.

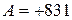
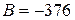
Алгебраическое сложение с использованием дополнительного кода. Для пояснения сущности излагаемого метода рассмотрим следующий пример. Пусть необходимо сложить два десятичных числа и . Так как второе слагаемое отрицательное число, то согласно приему, известному из школьной программы, для получения цифр суммы потребуется заем из старших разрядов. В цифровом устройстве эту операцию выполнять не обязательно. Искомый результат может быть получен, если отрицательное число преобразовать в дополнительный код и выполнить операцию поразрядного сложения (как при сложении положительных чисел).

При сложении складываются и двоичные цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса.

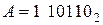
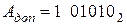
Дополнительный код отрицательного числа формируется по следующему правилу: инвертируются (производится замена 0 на 1 и 1 на 0) цифры всех разрядов отрицательного числа, кроме знакового разряда, и в младший разряд прибавляется 1. Например, если , то . Обратное преобразование из дополнительного кода в прямой код производится по тому же правилу.

Рассмотрим примеры выполнения операции сложения.

Пример 1. Пусть 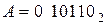и

Как указывалось выше, перенос из знакового разряда отбрасывается.

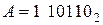
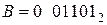
Пример 2. Изменим знаки слагаемых (по отношению к предыдущему примеру) и .

Таким образом, если результат сложения есть отрицательное число, то оно оказывается представленным в дополнительном коде.

Сложение десятичных чисел. Двоично-десятичные числа суммируются по правилам сложения двоичных чисел. Если при суммировании цифр тетрады полученная сумма больше девяти или формируется перенос из старшего разряда тетрады, то выполняется коррекция результата. При этом к полученной сумме прибавляется число шесть.

Пример 1. Сложить десятичные числа А=18 и В=19.

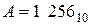
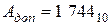
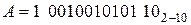
При суммировании отрицательных десятичных чисел отрицательные числа должны быть представлены в дополнительном коде. Дополнительный код отрицательного десятичного числа получается путем замены цифр разрядов (кроме знакового разряда) их дополнением до 9 и прибавлением затем в младший разряд 1. Например, если , то . При представлении десятичных чисел двоично-десятичным кодом дополнительный код получается следующим образом: сначала во все тетрады добавляется 0110₂ (6),

затем все цифры разрядов (кроме знакового разряда) инвертируются, и к младшему разряду прибавляется 1

Пример 2. Сложить десятичные числа А=836 и В=-256.

Умножение двоичных чисел. Операция умножения включает определение знака и абсолютного значения произведения.

Знаковый разряд произведения может быть получен суммированием по модулю 2 знаковых разрядов сомножителей.

Абсолютное значение произведения получается путем перемножения чисел без учета их знаков.

Пусть производится умножение чисел 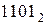и

Как видно из примера, операция умножения состоит из ряда последовательных операций сложения частичных произведений. Операциями сложения управляют разряды множителя: если в каком-то разряде множителя находится единица, то к сумме частичных произведений добавляется множимое с соответствующим сдвигом; если в разряде множителя – нуль, то множимое не прибавляется. Процесс суммирования можно начинать с младшего либо старшего частичного произведения.

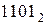
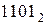
Ниже показаны процессы при умножении с суммированием частичных произведений, начиная со старшего (используется приведенный выше пример умножения чисел и ).

При умножении целых чисел для фиксации произведения в разрядной сетке должно предусматриваться число разрядов, равное сумме чисел разрядов множимого и множителя.

Источник