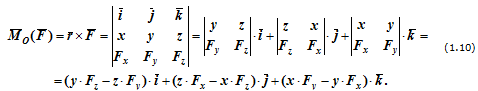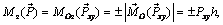Способ вычисления момента силы относительно оси

iSopromat.ru

Момент силы относительно оси – это характеристика вращательного действия силы на тело, закрепленное на оси, т.е. алгебраический момент проекции этой силы на плоскость, перпендикулярную к оси, относительно точки пересечения оси с этой плоскостью (рисунок 2).

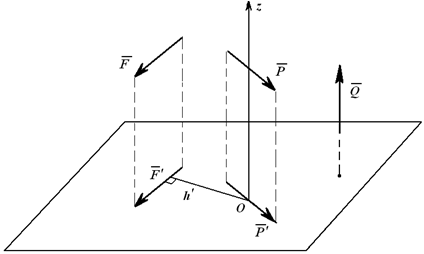
Момент силы относительно, например, оси O_z (рисунок 1), равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси ( F’) относительно точки пересечения оси с плоскостью, т.е.

Момент силы относительно оси – скалярная величина.

Моменты силы относительно координатных осей можно получить, расписав векторное произведение

Величины, стоящие в скобках, представляют собой моменты силы F относительно соответствующих осей.

Наш короткий видеоурок про момент силы с примерами:

Правило знаков

Момент считается положительным, если проекция силы на плоскость, перпендикулярную к оси, стремится вращать тело вокруг положительного направления оси против движения часовой стрелки, и отрицательным, если она стремится вращать тело по движению часовой стрелки:

где F_П – вектор проекции силы F на плоскость П, перпендикулярную к оси Oz, точка O – точка пересечения оси Oz с плоскостью П, h — плечо силы.

Это значит, что момент считается положительным, если мы смотрим навстречу оси и видим проекцию силы, стремящуюся повернуть плоскость чертежа в направлении против хода часовой стрелки.

Момент силы относительно оси равен нулю, если линия действия силы пересекает ось, т.е. h=0 (например M_z(P)), или сила параллельна оси, т.е. ее проекция на плоскость равна нулю, например, M_z(Q).

Свойства момента силы относительно оси

Момент силы относительно оси обладает следующими свойствами:

1. момент равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси;
2. момент равен нулю, если линия действия силы пересекается с осью. В этом случае равно нулю плечо силы.

Другими словами, момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.

Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]

Аналогом момента силы является момент пары сил.

Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.

Определение

Момент определяется как произведение силы F на плечо h:

Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.

Наш короткий видеоурок про момент силы с примерами:

Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки дает момент M=7×0,35=2,45 кНм.

Пример момента силы

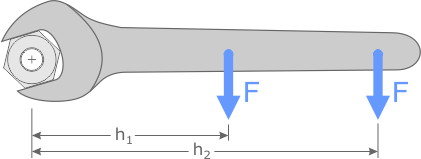
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.

Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.

Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h2>h1).

Плечом при этом служит расстояние от центра гайки до точки приложения силы.

Плечо момента силы

Рассмотрим порядок определения плеча h момента:

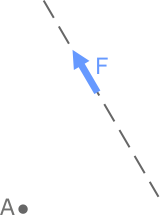
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.

Покажем линию действия силы F (штриховая линия)

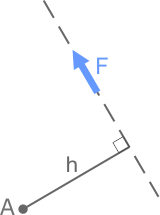
Проведем из точки A перпендикуляр h к линии действия силы

Длина отрезка h есть плечо момента силы F относительно точки A.

Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).

Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.

Примеры расчета момента силы

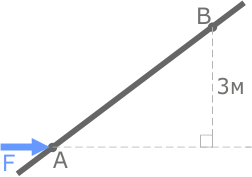
Сила расположена перпендикулярно оси стержня

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

Сила расположена под углом к оси стержня

Момент силы относительно точки B:

Известно расстояние от точки до линии действия силы

Момент силы относительно точки B:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Момент силы относительно оси

Рассмотрим, как определяется момент силы относи­тельно оси. Стремление силы вращать тело вокруг непо­движной оси зависит от величины силы, ее наклона и расстояния от оси.

Из опыта известно, что силы, про­ходящие через ось, и силы, параллель­ные оси, НЕ МОГУТ ВЫЗВАТЬ ВРАЩЕНИЯ ТЕЛА вокруг этой оси. Посмотрим на рисунок.

Ни сила Р₁, линия действия которой пересекает ось Oz, ни сила Р₂, параллельная оси, не смогут повернуть тело вокруг этой оси.

Для вращательного эффекта силы относительно закрепленной оси вводит­ся понятие момента силы относительно оси М_z (Р). Вращательный эффект силы относительно оси и выражается ее мо­ментом.

Пусть на тело в какой-то точке действует произ­вольная сила Р, не параллельная оси вращения Oz и не пересекающая эту ось. Проведем плоскость H, перпендикулярную оси Oz и проходящую через начало вектора силы. Разложим заданную силу Р на две составляющие: Р₁, расположенную в плоскости H, и Р₂, параллель­ную оси Oz.

Составляющая Р₂, параллельная оси Oz момента относительно этой оси не создает. Составляющая Р₁, действующая в плоскости H, создает момент относительно оси Oz или, что то же самое, относительно точки О. Мо­мент силы Р₁ измеряется произведением модуля самой силы на длину а перпендикуляра, опущенного из точки О на направление этой силы, т. е.

В выражение момента силы относительно оси входит не вся сила, а только ее составляющая, лежащая в пло­скости, перпендикулярной оси вращения.

Знак момента по общему правилу определяется на­правлением вращения тела: (+) при движении по часовой стрелке, (—) при движении против часовой стрелки (правило условно). При определении знака момента наблюдатель должен непре­менно находиться со стороны положительного направле­ния оси. На рисунке вверху момент силы Р относительно оси Oz положителен, так как для наблюдателя, смотрящего со стороны положительного направления оси (сверху), тело под действием заданной силы представляется вращаю­щимся вокруг оси по ходу часовой стрелки.

На рисунке внизу момент силы Р относительно оси Oz — величина отрица­тельная.

Рассмотрим частный случай.

В частном случае мо­мент силы Р, расположенной в плоско­сти H, относительно оси Oz, перпендикулярной этой плоскости, определится произведением полной ве­личины силы Р на ее пле­чо l относительно точки пересечения оси Oz и плос­кости H

Итак, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпенди­кулярную оси, и найти момент проекции силы на плоскость относительно точки пересечения оси с этой плоскостью.

Источник

Термех / УМК статика.кинематика / лекции / статика / проба1

2.Основные задачи статики

3.Основные понятия и определения статики твердого тела

4. Момент силы относительно центра и оси

5.Способы вычисления момента силы относительно оси

6.Алгебраический момент силы относительно центра

Механика  это наука, изучающая основные законы механического движения, т.е. законы изменения взаимного расположения материальных тел или частиц в сплошной среде с течением времени. Содержанием курса теоретической механики в техническом вузе является изучение равновесия и движения абсолютно твердых тел, материальных точек и их систем. Теоретическая механика является базой для многих обще-профессиональных дисциплин (сопротивление материалов, детали машин, теория машин и механизмов и др.), а также имеет самостоятельное мировоззренческое и методологическое значение. Иллюстрирует научный метод познания закономерностей окружающего нас мира – от наблюдения к математической модели, её анализ, получение решений и их применение в практической деятельности.

Курс теоретической механики традиционно делится на три части:

Статика  изучает правила эквивалентного преобразования и условия равновесия систем сил.

Кинематика  рассматривает движение тел с геометрической стороны, без учета сил, вызывающих это движение.

Динамика  изучает движение тел в связи с действующими на них силами.

Основные задачи статики:

Изучение методов преобразования одних систем сил в другие, эквивалентные данным.

Установление условий равновесия систем сил.

Источник

Момент силы относительно точки и оси

Моментом силы относительно точки O называют величину, равную векторному произведению радиус-вектора , проведенного из точки O в точку приложения силы (рис. 2.1), на эту силу

. (2.1)

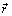
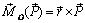
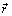
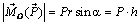
Этот вектор приложен в точке O и направлен перпендикулярно плоскости, содержащей векторы и в ту сторону, откуда вращение тела, вызываемое силой вокруг точки O, представляется происходящим против часовой стрелки.

, (2.2)

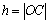
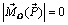
где – плечо силы относительно точки O, равное расстоянию от этой точки до линии действия силы . Из формулы (2.2) следует, что , если h = 0, т.е. если линия действия силы проходит через точку О.

Обозначим через x, y, z координаты точки приложения силы, 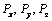– проекции силы на координатные оси. Тогда момент силы можно представить следующим образом

, (2.3)

откуда следует, что проекции момента силы на координатные оси равны

. (2.4)

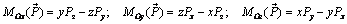
Моментом силы относительно оси называют величину, равную проекции на эту ось момента силы, взятого относительно некоторой точки оси

. (2.5)

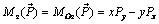
Момент силы относительно оси не зависит от выбора точки O на оси, так как ни одна из величин в правой части формулы (2.5) не зависит от положения начала координат при параллельном перемещении осей x и y.

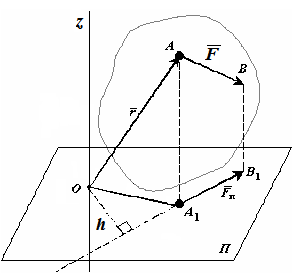
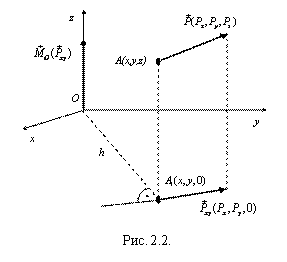
Проекцией силы на плоскость называют вектор, начало и конец которого совпадают с проекциями начала и конца вектора силы на эту плоскость. На рис. 2.2 показана проекция силы на плоскость xОy. Так как проекции сил и , а также точек их приложения на оси x и y одинаковы, момент силы относительно точки O может быть вычислен по формуле (2.3), где следует положить, что z = 0 и ,

.

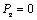
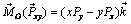
Этот момент направлен вдоль оси z, а его проекция на эту ось совпадает с моментом силы относительно оси z:

где h – плечо силы относительно точки O.

Таким образом, можно сформулировать следующее правило вычисления момента силы относительно оси z:

1) выберем на оси z произвольную точку и построим плоскость, перпендикулярную этой оси;

2) спроецируем силу на эту плоскость;

3) определим плечо проекции силы;

4) вычислим момент силы относительно оси z по формуле

. (2.6)

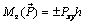
В формуле (2.6) знак «плюс» ставим в том случае, если с положительного направления оси z поворот тела вокруг этой оси виден направленным против часовой стрелки, знак «минус» – в противном случае. Аналогично вычисляют моменты силы относительно других координатных осей.

Из формулы (2.6) следует, что момент силы относительно оси равен нулю в двух случаях:

1) если сила параллельна оси, т.е. проекция = 0;

2) если линия действия силы пересекает ось, т.е. плечо h = 0.

Оба случая можно объединить: момент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось лежат в одной плоскости.

Источник