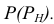Способ вспомогательных секущих плоскостей алгоритм решения задач

Способ вспомогательных секущих плоскостей алгоритм решения задач

Простейшая позиционная задача с использованием этого метода — оценка взаимного расположения прямой и плоскости. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в , последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a (рис.150).

Рисунок 1 50. Метод вспомогательных секущих плоскостей

Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости a , параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю, когда прямая а пересекает плоскость a .

Таким образом возможны три случая относительного расположения прямой и плоскости:

Вспомогательные секущие плоскости чаще всего выбирают перпендикулярными или параллельными плоскости проекций.

Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:

если образующие (окружности) расположены в общих плоскостях уровня;

если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;

линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.

Источник

Метод плоскостей | AutoCAD

В этом уроке рассмотрим одну из самых распространенных задач начертательной геометрии – построение пересечения поверхностей методом секущих плоскостей и способ ее решения средствами AutoСАD.

Метод секущих плоскостей, немного теории

Вкратце суть метода секущих плоскостей состоит в том, что для построения линии пересечения двух поверхностей строятся вспомогательные плоскости (обычно – параллельные одной из плоскостей проекций), которые пересекают заданные поверхности, образуя при этом простые геометрические фигуры.

Точки взаимного пересечения заданных поверхностей будут общими точками двух кривых, образованных пересечением секущей плоскости с каждой из поверхностей.

Условия задачи

Зададим условия: пусть необходимо построить пересечение полусферы и конуса, расположенных таким образом:

Размеры показаны для наглядности, проставлять их на чертеже не нужно.

Решение

Строим секущие плоскости, вид с боку

Очевидно, что для тел вращения удобно использовать плоскости, перпендикулярные осям этих тел. В нашем случае вспомогательные плоскости будут параллельными горизонтальной плоскости. Изобразим их на фронтальном виде (в нашем случае верхняя из плоскостей проходит через явно видимую верхнюю точку пересечения конуса и полусферы, в других случаях для нахождения этой точки потребуются дополнительные построения):

Секущие плоскости, вид сверху

Теперь перенесем линии пересечения секущих плоскостей с каждой из поверхностей на вид сверху. Очевидно, что горизонтальные плоскости пересекают каждое из тел по окружностям, центры которых находятся на одной вертикали с центрами тел. Радиусы этих окружностей легко переносятся на вид сверху с образующих каждой поверхности. Вот эти окружности для полусферы:

Точки пересечения секущих плоскостей

Отметим для наглядности общие точки для каждой из пар окружностей, образованных одной плоскостью:

Видно, что в районе верхней точки построение недостаточно «информативно», т.е. будет полезным построить еще одну секущую плоскость:

Вот еще две точки, заданные этой плоскостью:

Линия пересечения

Соединив на виде сверху полученные точки сплайном (команда Сплайн), мы получим приближенную линию пересечения двух поверхностей:

Остается перенести линию на фронтальный вид. Сделать это совсем несложно: нужно перенести каждую из точек с вида сверху на соответствующую секущую плоскость на фронтальном виде. Линии построения выделены желтым цветом:

Поскольку исходные поверхности (и, соответственно, линия их пересечения) симметричны относительно плоскости, параллельной фронтальной плоскости проекции, достаточно перенести только половину точек. В нашем частном случае невидимая на фронтальном виде часть кривой «спрятана» за видимой, а верхняя точка является точкой разделения видимой и невидимой частей.

Проверка вида линии пересечения

Полезно проверить правильность наших построений средствами 3D-моделирования. Построим соответствующие фигуры, перейдя предварительно к интерфейсу 3D- моделирование , и сравним полученную модель с построением (для этого удобнее объединить объекты командой Объединить).

Резюме

Как видим, наше построение довольно точно передает реальную линию пересечения поверхностей вращения. И хотя современные средства моделирования позволяют строить такие пересечения гораздо быстрее, рассмотренные нами принципы очень полезны для понимания «механики» геометрических построений, без которого любой, даже самый современный инструмент 3D-моделирования превращается в сложную и непонятную игрушку.

Источник

Способ вспомогательных секущих плоскостей в начертательной геометрии с примером

Способ вспомогательных секущих плоскостей:

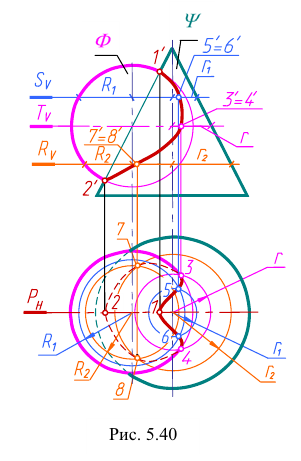
Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения сферы с конусом вращения (рис.5.40).

Для построения линии пересечения заданных поверхностей в ка­честве вспомогательных плоскостей необходимо использовать фронтальную плоскость Р и ряд горизонтальных плоскостей (S, Т, R).

Построение начинаем с определения проекций характерных точек. Проводим фронтальную плоскость

Вспомогательные горизонтальные плоскости пересекают сферу и конус по окружностям.

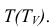
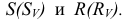
Проекции 3′ и 4′ точек, лежащих на экваторе сферы, находим с помощью горизонтальной плоскости Она проходит через центр сферы. Плоскость пересекает сферу по экватору и конус по окружности радиуса В пересечении горизонтальных проекций этих линий и нахо­дим горизонтальные проекции 3 и 4 . Горизонтальные проекции точек 3 и 4 являются точками границы видимости линии пересечения на этой проекции. Промежуточные точки (точки 5, 6, 7, X) находим с помощью вспомогательных горизонтальных плоскостей Полученные точки соединим плавной кривой линией с учетом видимости.

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Способ вспомогательных сфер
• Выполнение и оформление чертежей по ГОСТ и ЕСКД
• Виды в инженерной графике
• Разрезы в инженерной графике
• Построение проекций линий пересечения конуса плоскостью
• Развертка поверхности конуса
• Шаровая поверхность
• Винтовые поверхности

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Конспект лекций по курсу “Начертательная геометрия и инженерная графика” Кемерово 2002

Главная > Конспект лекций

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

9.2.1. Применение метода секущих плоскостей при

На рис.9.3. даны конус и полусфера.

В данном случае в качестве вспомогательных секущих плоскостей необходимо выбрать плоскости, параллельные горизонтальной плоскости проекций, так как такие плоскости пересекают конус и полусферу по окружностям.

тобы начать построение линии пересечения необходимо начать построение линии пере-сечения необходимо найти опор-ные точки: самую высокую и самую низкую в данном случае. В других случаях это может быть самая левая или самая правая точки. Пересечем обе поверхности плоскостью V и проходящей через оси вращения поверхностей. В результате получим линии пересечения, которые являются фронтальными очерками данных поверхностей. Точка пересечения очерков 1 является точкой, принадлежащей линии пересечения.

Так как основания обеих поверхностей лежат в одной плоскости, то точки пересечения окружностей 2 и 3 также являются общими точками для данных поверхностей.

Точки 1,2,3 являются опорными, точка 1 — самая высокая, точки 2, 3- самые низкие. Теперь обе поверхности пересечем плоскостью , расположенной ниже точки 1 и выше точек 2 и 3. Эта плоскость  пересечет обе поверхности по окружностям n 2 и m 2 найдем точки пересечения полученных окружностей n 2 m 2 = 4, :n 2  m 2 = 5.

Точки 4,5 принадлежат линии пересечения конуса и полусферы. Повторив это действие, необходимое число раз, построим линию пересечения данных поверхностей.

9.3. Метод концентрических сфер

В этом случае в качестве вспомогательных секущих поверхностей выбираются концентрические сферы.

Применение этого метода основано на следующем свойстве: Две поверхности вращения, имеющие общую ось (соосные поверхности), пересекаются по окружностям. Действительно, кривая m образует поверхность вращения с осью вращения i, кривая n образует вторую поверхность вращения с той же осью i. Если mn = А, то точка А опишет окружность, которая является общей для обеих поверхностей, следовательно, является линией их пересечения. (Рис.9.4.)

Если ось i перпендикулярна плоскости Н, то окружность, описываемая точкой А, проецируется на фронтальную плоскость проекций в отрезок, а на горизонтальную плоскость в окружность.

Из сказанного можно сделать следующие выводы:

1. Для того, чтобы вспомогательная секущая сфера пересекала по окружностям две заданные поверхности вращения, центр сферы должен лежать в точке пересечения осей этих поверхностей.

2. Если оси заданных поверхностей вращения параллельны плоскости проекций, то окружности пересечения вспомогательной секущей сферы с этими поверхностями проецируется на эту плоскость в отрезки.

Теперь можно сформулировать условия, необходимые для применения метода концентрических секущих сфер:

1. Данные поверхности должны быть поверхностями вращения;

2. Оси вращении данных поверхностей должны пересекаться;

3. Плоскость, проходящая через оси вращения данных поверхностей, должна быть параллельна какой — нибудь плоскости проекций.

Построение линии пересечения начинается с построения опорных точек (Рис.9.5.). Чтобы построить опорные точки надо построить сферу минимального радиуса. Сфера минимального радиуса вписана в одну поверхность и пересекает вторую.

Общие точки С и Д окружности касания с конусом и окружности пересечения с цилиндром являются опорными точками. К опорным точкам относятся также точки пересечения фронтальных очерков данных поверхностей. Отрезок OF где f наиболее удаленная от точки О точка пересечения очерков данных поверхностей определяет сферу максимального радиуса.

Для построения промежуточных точек необходимо выбрать сферу радиуса R, где R min max .

1. Для этого из центра О= i 2  i 1 нужно провести окружность произвольного радиуса, являющейся проекцией сферы.

2. Построим линию пересечения сферы с конусом. Это будет окружность, которая на фронтальную плоскость проекций проецируется в отрезок. Затем построим линию пересечения сферы с цилиндром. Это тоже окружность, которая тоже проецируется в отрезок, точки пересечения А и В данных окружностей являются точками пересечения цилиндра и конуса. Для построения других промежуточных точек нужно из точки О описать ряд концентрических окружностей и проделать те же построения.

9.4. Метод эксцентрических сфер

Рассмотрим пересечение конуса и тора (рис.9.6.). Ось конуса параллельна V, а ось вращения тора j перпендикулярна V. Ocь конуса i и круговая ось тора q лежат в общей плоскости симметрии , параллельной плоскости V. По отношению к плоскости V плоскость  является главной меридиональной плоскостью Поэтому плоскость  пересекает конус по образующим, а тор — по двум дугам окружности. Оба сечения проецируются на плоскости V очерковыми линиями проекций тора и конуса. Очерковые линии пересекаются в точках 1 и 2, которые являются проекциями точек 1 и 2, принадлежащими линии l пересечения рассматриваемых поверхностей. Эти точки являются опорными. Проведем через ось тора j плоскость Г. Плоскость Г пересечет тор по окружности р, а его круговую ось — в точке С. Окружность р проецируется на плоскость V отрезком р , равным ее диаметру.

Определим точки 3 и 4 пересечения окружности р с поверхностью конуса. Для этого заключим окружность р в вспомогательную сферу. Центр сферы должен находиться на оси конуса. Только в этом случае сфера пересечет конус по окружности, по тому проекцию центра сферы О найдем как точку пересечения касательной СО к центровой окружности тора с осью конуса. Радиус сферы равен R. Сфера пересечет конус по окружности р ь Окружность кольца р и окружность p 1 конуса располагаются на одной сфере и, следовательно, пересекается в точках 3 и 4, принадлежащих искомой линии пересечения конуса и тора.

Другие точки, принадлежащие пересечению конуса с тором, строятся по только что рассмотренному алгоритму с помощью других радиальных плоскостей.

9.5. Особые случаи пересечения двух поверхностей 2-го

Теорема 1 . Если две поверхности 2-го порядка пересекаются по одной плоской кривой, которая тоже будет плоская. (Рис.9.7 . )

Теорема 2 . Если две поверхности 2-го порядка имеют две точки соприкосновения, то линия их пересечения распадается на две кривые 2-го порядка, плоскости которых проходят через прямую, соединяющую точки касания. (Рис.9.8 . )

Теорема 3 . Если две поверхности 2-го порядка описаны около третьей поверхности 2-го порядка или вписаны в нее, то они пересекаются по двум плоским кривым, плоскости которых проходят через прямую, соединяющую точки пересечения линий прикосновения. Эта теорема носит название теоремы Монжа. (Рис.9.9.).

Иллюстрацией к теореме 1 является рис.9.7, на котором изображено пересечение эллиптического цилиндра и конуса, имеющих общую окружность основания, Вторая кривая их взаимного пересечения также плоская, которая расположена в плоскости перпендикулярной V.

Иллюстрацией к теореме 2 является рис,9,8., на котором цилиндрическая поверхность соприкасается в точках А и В с эллиптическим цилиндром. В соответствии с теоремой линия пересечения поверхностей распа-дается на две плоские кривые (эллипсы), плоскости которых будут перпендикулярны V. Фронтальные проекции эллипсов проходят через точки пересечения проекций очерков поверхностей и через проекцию точек соприкосновения А =В. Горизонтальные проекции эллипсов могут быть построены как плоские сечения конической или цилиндрической поверхности

На рис.9.9. показано пересечение цилиндра и конуса по плоским кривым. Обе поверхности описаны около одной сферы и пересекаются по двум эллипсам, плоскости которых перпендикулярны V.

9.6. Построение линии пересечения поверхностей, когда

Поверхности цилиндра и призмы иногда могут располагаться по отношению к плоскостям проекций таким образом, что образующие цилиндра или боковые ребра и боковые грани призмы окажутся перпендикулярными какой — то плоскости проекций. Такое положение поверхности называется проецирующим . Проекцией такой поверхности является окружность, если это цилиндр, или многоугольник, если это призма. В таком случае построение линии пересечения поверхностей упрощается.

Рассмотрим пример: необходимо построить линию пересечения двух цилиндров, один из которых расположен вертикально. Образующие такого цилиндра перпендикулярны плоскости Н. Второй полуцилиндр расположен таким образом, что образующие этого полуцилиндра перпендикулярны плоскости W. (Рис.9.10.)

При таком расположении цилиндров горизонтальная проекция линии пересечения совпадает с окружностью — горизонтальной проекции цилиндра с вертикальной осью, а профильная проекция линии пересечения совпадает с полуокружностью профильной проекцией полуцилиндра с горизонтальной осью. Это выполняется потому что вертикальный цилиндр занимает горизонтально — проецирующее положение, а полуцилиндр — профильно проецирующее положение. Построение фронтальной проекции линии пересечения осуществляется по правилам построения третьей проекции точки, если известны две ее другие проекции.

Рассмотрим еще один пример: построим линию пересечения конуса с цилиндром. Цилиндр занимает горизонтально – проецирующее положение, следовательно, горизонтальной проекцией цилиндра является окружность, горизонтальная проекция линии пересечения цилиндра и конуса совпадает с горизонтальной проекцией цилиндра, т.е. окружностью. Чтобы построить фронтальную проекцию линии пересечения необходимо выбрать точки на окружности. Сначала выбираем характерные точки линии пресечения. Это точки 1,2,3,4,5,6, Точки 1,6 являются крайними. Отмечают их горизонтальные проекции 1,6. Так как это точки лини пересечения поверхностей, то они одновременно принадлежат цилиндру и конусу. Точки 1,6 принадлежат окружности основания конуса.

Используя эту принад-лежность, находим фронтальные проекции точек 16. Точка 3 так же является характерной, так как она принадлежит плоскости , проходящей через оси вращения данных поверхностей. В этой плоскости находятся самая вы-сокая и самая низкая точка линии пересечения. Точка 3 находится на окружности, принадлежащей конусу. Эта окружность на горизонтальную плоскость проекции проецируется в натуральную величину а на фрон-тальную плоскость — в отрезок. Выбрав горизонтальную проек-цию 3, проводим окружность, находим фронтальную проекцию этой окружности, на ней находим точку 3. (Нахождение фрон-тальной проекции окружности видно из рис.9.11.). Точка 2 — самая дальняя, 4 — самая правая, 5 — самая близкая. Построив харак-терные точки, проекцию линии пересечения построить еще сложно, можно выбрать промежуточные (например: 4 1 ), и осуществить точно такие построения.

В других случаях построение осуществляется аналогично. Одна проекция линии совпадает с проекцией проецирующей поверхности, а для построения f второй проекции линии пересечения надо использовать принадлежность линии второй поверхности.

Чтобы построить точку, принадлежащую поверхности, надо через данную точку провести линию, принадлежащую данной поверхности. Это может быть образующие, или окружности в зависимости от поверхности.

Р

9.7. Пересечение поверхности плоскостью

9.7.1. Конические сечения

(сечения прямого кругового конуса плоскостью)

Если секущая плоскость не параллельна ни одной из образующих конуса, то в сечении получается эллипс.

Если секущая плоскость параллельна одной образующей, то в сечении будет парабола.

Если пересечь конус плоскостью, параллельной двум его образующим, то в сечении получится гипербола.

Признаки, по которым можно определить вид кривой, даны на рис.9.15.

Чтобы построить С, надо построить фронтальную проекцию образующей SK. Это будет прямая SК. На ней получим точку С. Аналогичным способом строим точку D. Берем D на образующей SN, строим SN, затем точку D. Эту точку нужно строить обязательно, так как в этой точке происходит переход с видимой на невидимую сторону поверхности (рис.9.18.),

9.7.2. Сечение сферы

плоскостью частного положения

Сфера пересечена фронтально- прое-цирующей плоскостью (рис.9.19.)

кружность, по которой плоскость  пересекает сферу, на плоскость Н проецируется в эллипс. На фронтальную плоскость проекций эта окружность проецируется в отрезок 12, лежащей на следе  v . Строим точки 1 и 2, это горизонтальные проекции самой высокой и самой низкой точками сечения. Большая ось эллипса на горизонтальной плоскости проекций определяется точками 5 и 6, которые получаются при пересечении плоскости Т, проходящей через центр сферы, перпендикулярной плоскости .

Для построения горизонтальных проекций точек воспользуемся параллелями сферы, проходящими через выбранные точки. Обязательно нужно выбрать точки 3 и 4, лежащие на экваторе, так как являются точками перехода с видимой на невидимую сторону поверхности (рис.9.19.).

При изучении построения разверток поверхности рассматривают как гибкую нерастяжимую пленку. Некоторые поверхности при изгибании можно совместить с плоскостью без разрывов и склеивания. Такие поверхности называют развертывающимися, а полученную плоскую фигуру — разверткой. Поверхности, которые нельзя совместить с плоскостью, относятся к неразвертываемым.

Построение разверток имеет большое практическое применение, так как позволяет изготавливать разнообразные изделия из листового материала путем его изгибания.

10.1. Основные свойства разверток поверхностей

Каждой точке (фигуре) на поверхности соответствует точка (фигура) на развертке и наоборот.

На основании этого можно сформулировать следующие свойства:

1. Длины двух соответствующих линий поверхности и ее развертки равны между собой. Следствие: замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают одинаковую площадь.

2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке.

3. Прямой на поверхности соответствуют прямая на развертке.

4. Параллельным прямым на поверхности соответствуют также параллельные на развертке

10.2. Развертка поверхности многогранников

Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью.

Существуют три способа построения развертки многогранных поверхностей:

1) Способ треугольников (триангуляции);

2) Способ нормального сечения;

3) Способ раскатки.

10.2.1. Способ треугольников (триангуляции)

Этот способ применяется для построения развертки пирамидальных поверхностей. Сущность его: последовательное совмещение всех граней пирамиды (грани представляют собой треугольники) с плоскостью.

Пример: Построить развертку боковой поверхности пирамиды SABC.

Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников — граней пирамиды. Поэтому построение развертки поверхности пирамиды сводится к определению действительной величины ребер пирамиды и построению по трем сторонам треугольников — граней пирамиды (Рис.11.1.).

О

пределение дейст-вительной длины ребер пирамиды выполнено с помощью вращения их вокруг оси i (iS и i  H). Путем вращения реб-ра пирамиды совме-щаются с плоскостью  (плоскость ||V и i). После того, как будут определены действительные вели-чины ребер [SA 2 ], [SB 2 ], [SC 2 ], прис-тупают к построению развертки. Дня этого из произвольной точ-ки S o проводят произ-вольную прямую а. Откладывают на ней от точки S 0 [S o A o ][SA 2 ]. Из точ-ки а о проводят дугу радиусом r 1 = |АВ, а из точки S o — радиусом r i =SB 2 . Пересе-чение дуг укажет по-ложение вершины В о треугольника S 0 A 0 B 0 (треугольник S o A o B o = треугольник SAB — грани пирамиды). Аналогично находятся точки S o и а о . Соединив точки A o B o C o A 0 S o , получим развертку поверхности пирамиды SABC.

10.2.2. Способ нормального сечения

Способ применяется для построения развертки призматических поверхностей при условии, если ребра призмы, параллельны какой -либо плоскости проекции. Если ребра занимают произвольное положение, то перед построением развертки следует преобразовать чертеж.

Пример: Построить развертку наклонной трехгранной призмы ABCDEF (рис.10.2.).

Пересечем призму ABCDEF плоскостью , пер-пендикулярной к боковым ребрам призмы. Построим се-чение заданной призмы этой плоскостью треугольника 123. Определяем дейст-вительную величину сторон треугольника 123. В произ-вольном месте чертежа проводим прямую а. От произвольной точки 1 0 , взя-той на этой прямой, отк-ладываем отрезки [1 о 2 о ], [2 о З о ], [З о 1 0 ], конгруентные сторонам треугольника 123. Через точки 1 0 2 0 3 о 1 о про-водим прямые, пер-пендикулярные к прямой а, и отк-ладываем на них от точек 1 о ,2 о , З о , 1 о от-резки, конгруентные соответствующим дей-ствительным вели-чинам отрезков боко-вых ребер ([1А], [1Д, [2В], [2Е], . и т.д.). Полученные точки А 0 В 0 С о А 0 и D 0 E o F o D 0 соединяемы прямыми.

лоская фигура A o B o C o A о D o F o T o D o представляет собой развертку боковой поверхности призмы.

Чтобы получить полную развертку призмы, необходимо к развертке боковой поверхности пристроить основания призмы треугольников А о В о С о и D o E o F o , предварительно определив их действительную величину.

10.2.3. Способ раскатки

Этот способ используют для построения развертки призмы в том случае, если основание призмы параллельно какой- либо плоскости призмы, а ее ребра параллельны другой плоскости проекции.

Пример: Построить развертку боковой поверхности наклонной трехгранной призмы ABCDEF (Рис.10.3.).

римем за плоскость развертки плоскость , проходящую через ребро AD, параллельную фронтальной плоскости проекции. Совместим грань ADEB с плоскостью . Для этого мысленно разрежем поверхность призмы по ребру AD, а затем осуществим поворот грани ADEB вокруг ребра AD (AD).

Для нахождения совмещенного с плоскостью  положения ребра В 0 Е 0 из точки В проводим луч, перпендикулярный к AD, и засекаем на нем дугой радиуса АВ, проведенной из центра А, точку В 0 . Через В 0 проводим прямую В о Е о , параллельную (АD).

Принимаем совмещенное положение ребра В о Е о за новую ось и вращаем вокруг нее грань BEFC до совмещения с плоскостью .

Для этого из точки С проводим луч, перпендикулярный к совмещенному ребру B 0 E 0 а из точки В 0 — дугу окружности радиусом, равным ВС; пересечение дуги с лучом определит положение точки С о .

Через С о проводим C 0 F 0 параллельно В 0 Е 0 . Аналогично находим положение ребра A 0 D 0 Соединив точки AB o C o F o DE 0 F 0 D 0 прямыми, получим фигуру AB o C o A o D o F o E o D — развертку боковой поверхности призмы.

Для получения полной развертки призмы, достаточно к какому — либо из звеньев ломаной линии АB о С о А о и DE o F o D o построить треугольники основания А о В о С о и D o E o F o .

10.3. Построение разверток конических и

Для построения развертки конических и цилиндрических поверхностей применяют три описанных выше способа. При этом конические и цилиндрические поверхности заменяют (аппроксимируют) пирамидальными и призматическими поверхностями с произвольным числом граней. Очевидно, что чем больше граней, тем точнее развертка поверхности.

рием аппроксимации конической поверхности пирамидальной показан на рис.10.4., цилиндрической на рис.10.5.

ЛИТЕРАТУРА

1. Фролов С.А. Начертательная геометрия. — М.: Машиностроение, 1983.

2. Крылов Н.Н., Иконникова Г.С., Николаев Н.М., Лаврухина Н.М. Начертательная геометрия. — М.: Высшая школа, 1990

3. Гордон В.О., Семенов-Огневский М.А. Курс начертательной геометрии. — М.: «Наука» Главная редакция физико-математической литературы, 1988

4. Посвянский А.Д. Краткий курс начертательной геометрии. -М.: Высшая школа, 1974

5. Чекмарев А.А. Начертательная геометрия. — М.: Просвещение, 1987

6. Лагерь А.Н., Колесникова Э.А. Инженерная графика. — М.: Высшая школа, 1985

7. Тевлин A.M. Курс начертательной геометрии на базе ЭВМ. -М.: Высшая школа, 1983

8. Иванов Г.С. Начертательная геометрия. — М.: Машиностроение, 1995

9. Кузнецов Н.С. Начертательная геометрия. — М.: Высшая шко-ла,1981

10. Глоголовский В.В. Гринева Б.М., Гнатюк М.О. Начертательная геометрия на алгоритмической основе. — Львов.: Издательство при Львовском государственном университете издательского обьединения «Вища школа», 1978

11. Фролов С.А. Сборник задач по начертательной геометрии. -М.: Машиностроение, 1978

12. Четверухин Н.Ф. и др. Курс начертательной геометрии. — М.: Высшая школа, 1968

13. Русскевич Н.Л. Начертательная геометрия. — Киев.: Вища школа, 1970

14. Бубенников А.В., Громов М.Я. Начертательная геометрия. -М.: Машиностроение, 1973

Источник