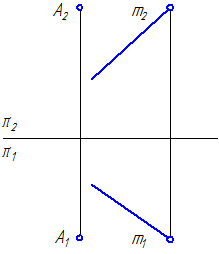Способ вращения вокруг горизонтали

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

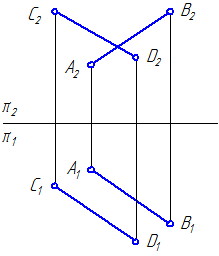
Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

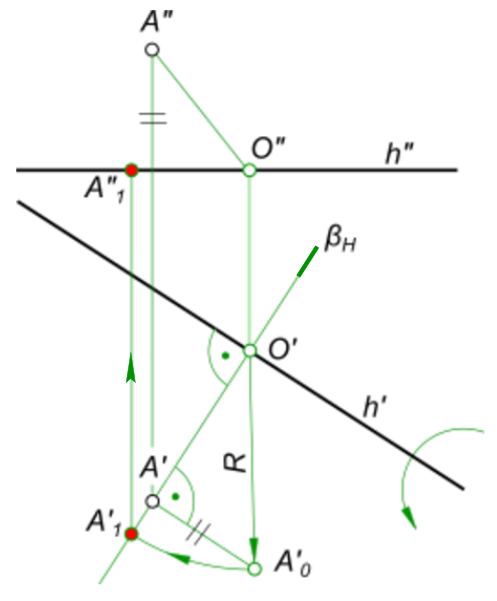
Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник

Вращение вокруг горизонтали

Вращение вокруг горизонтали плоскости, дает возможность перевести ее в положение, параллельное плоскости H, и получить неискаженный вид горизонтальной проекции. Вращение плоскости вокруг фронтали позволяет перевести ее в положение, параллельное плоскости V, что обеспечит получение неискаженного вида фронтальной проекции. При таком положении плоскости ортогональная проекция любой принадлежащей ей фигуры на одну из плоскостей проекций будет конгруентной оригиналу и, следовательно, позволит определить все метрические характеристики фигуры по этой ее проекции.

Когда происходит вращение вокруг горизонтали, окружность, представляющая траекторию точки, будет проецироваться на плоскость H в отрезок прямой, перпендикулярной горизонтальной проекции горизонтали.

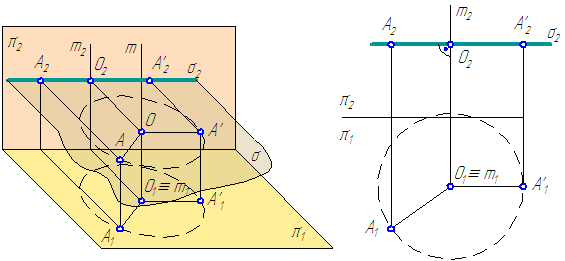
Вращение вокруг горизонтали точки A

Вращение точки вокруг фронтали плоскости α(b ∩ d)

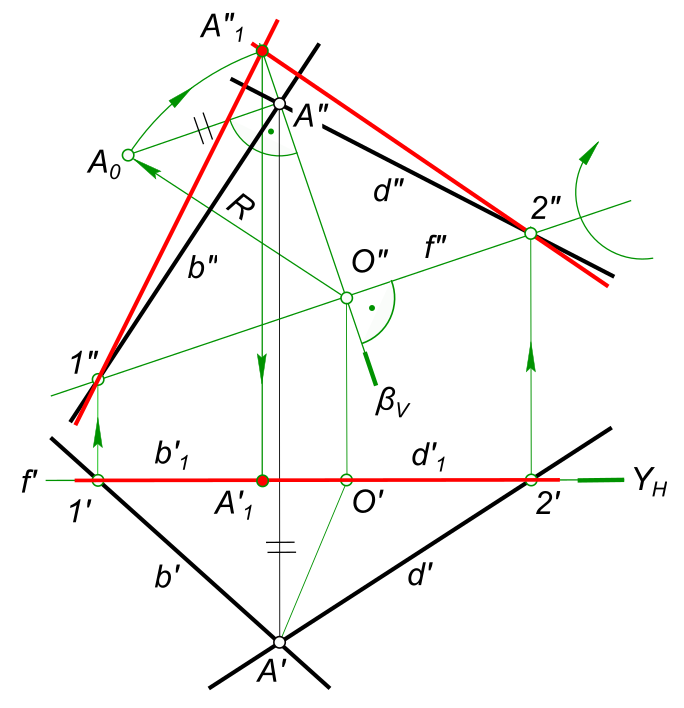
Плоскость α, заданную пересекающимися прямыми b и d, переводим в положение параллельное плоскости V: — проводим горизонтальную проекцию f` фронтали f, по точкам 1 и 2 определяем положение фронтальной проекции f» фронтали f; — через точку A проводим фронтально проецирующую плоскость β перпендикулярную фронтали f и на их пересечении определяем центр вращения O(O» ⇒ O`); — определяем радиус вращения R, как гипотенузу прямоугольного треугольника O»A»A₀; — из центра O» проводим дугу радиусом O»A₀ и на ее пересечении с прямой (O»A») находим положение проекции A»₁, а затем и A`₁. Точка A₁ совместно с прямой f (точками 1, 2) определяет плоскость α₁║V.

Используя вращение вокруг горизонтали

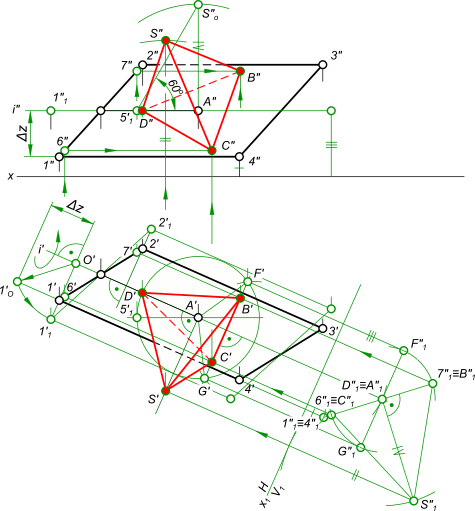
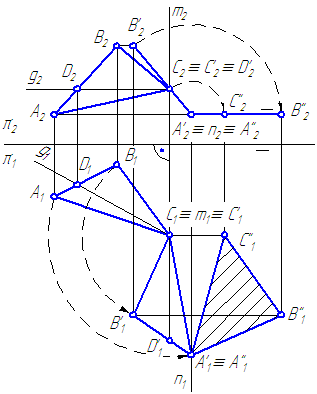
построить правильную треугольную пирамиду с основанием в плоскости 1-2-3-4 и центром основания в точке A. Наклон боковых ребер к основанию равен 60°. Правильная треугольная пирамида имеет в основании равносторонний треугольник и одинаковые боковые грани. Плоскость основания 1-2-3-4 образована двумя парами параллельных прямых 1-3, 2-4 и 1-2, 3-4, причем стороны 1-3 и 2-4 представляют собой горизонтали так как их фронтальные проекции параллельны оси x. Центр основания в точке A, аналогично определяем расположенным на горизонтали. Плоскость основания 1-2-3-4 занимает общее положение. Составим план решения: 1. Построение в плоскости основания 1-2-3-4 равностороннего треугольника — основания пирамиды; 2. Определение высоты пирамиды построением заданного угла 60 между боковыми ребрами и основанием; 3. Построение проекций вершин пирамиды; 4. Определение видимости.

План решения выполняем пошагово: 1. Переводим плоскость основания 1-2-3-4 в частное горизонтальное положение вращением вокруг горизонтали i, проходящей через точку A, находя при этом ее новое положение 11-21-31-41; 2. В плоскости основания 11-21-31-41 проводим окружность максимально возможного радиуса и через ее центр A проводим фронталь 51-A; 3. На фронтальной плоскости проекций строим боковое ребро задавая угол 60° наклона его к основанию; 4. Задав положение одной из вершин основания в точке D на оси вращения i, Находим остальные вершины основания пирамиды F и G, расположенными на равном расстоянии друг от друга на дуге окружности; 5. Построение проекций вершин основания пирамиды B и C и вершины S выполняем способом перемены плоскости проекций: а) плоскость основания пирамиды горизонтальна — D1, F1 и G1; б) плоскость основания пирамиды первоначального положения проходит через точки 1″1=4″1, D»1=A»1; в) на направлении перпендикуляра из точки A»1 откладываем высоту пирамиды и находим S»1; г) в пересечении линий проекционной связи точек S»1, перпендикуляра n` к плоскости основания находим S`1; д) в пересечении линий проекционной связи точек B»1 и C»1 c F`- G`находим точки B` и C`; е) в пересечении линий проекционной связи точек B` и C` c горизонталями проходящими через 6 и 7 находим точки B» и C»; ж) отложив от оси x по линии проекционной связи точки S отрезок II находим точки S»; з) определение видимости.

Вращение вокруг горизонтали применяется для решения задачи №3 по определению натуральной величины боковой грани SAC пирамиды: Графическая работа 6.

Источник

Вращение вокруг горизонтали или фронтали

При вращении точки в пространстве вокруг горизонтали горизонтальная проекция точки перемещается по прямой, перпендикулярной проекции горизонтали, а фронтальная — по эллипсу (искаженной проекции окружности вращения). При решении задач этот эллипс не строится.

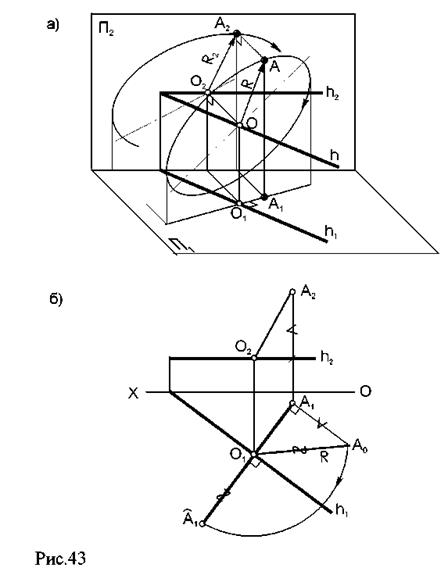
Отрезок О₁А₀ – натуральная величина радиуса вращения точки А; отложив его на линии, перпендикулярной h₁, мы точку перемещаем в плоскость, параллельную горизонтальной плоскости проекций П₁ (рис.43)

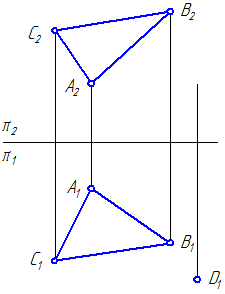
Пример: Определить натуральную величину треугольника АВС (рис. 44).

За ось вращения i примем горизонталь h и повернем треугольник АВС вокруг нее как вокруг оси вращения до положения, параллельного плоскости П₁; точки А и 1 остаются неподвижными, а В и С вращаются. Способом прямоугольного треугольника определяем натуральные величины радиусов вращения, а траектории движения на П₁ перпендикулярны линии i₁.

Новое положение точки С — С₀ можно найти как пересечение двух траекторий вращения С₁О_С1 и В₀1₁, которая уже лежит в плоскости, параллельной горизонтальной плоскости проекций.

Плоскопараллельное перемещение (вращение без указания оси).

При вращении прямой линии, плоскости и любого другого объекта, их проекции на плоскости, перпендикулярной оси вращения, сохраняют свою величину и форму. Вторые проекции объекта перемещаются по прямым, перпендикулярным проекции оси вращения (или линиям связи). Эти свойства проекций позволяют перемещать данный объект в частное положение, используя свободное поле эпюра, без нанесения проецирующих осей вращения.

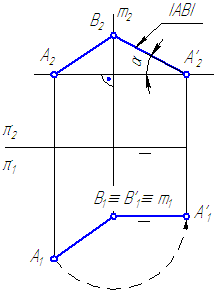
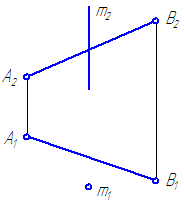
На рис. 45 отрезок АВ повернем на некоторый угол вокруг условной оси, перпендикулярной горизонтальной плоскости проекций. Из положения АВ он переместится в положение А 1 В 1 ; горизонтальная проекция отрезка А₁В₁ займет положение А₁ 1 В₁ 1 ; |А₁В₁|= |А₁ 1 В₁ 1 |.

Пример. Определить натуральную величину отрезка AB (рис. 46).

Одна проекция отрезка ABдолжна быть расположена параллельно оси Х. Повернем A₁B₁, до такого положения, при этом фронтальные проекции точек переместятся по линиям, параллельным оси Х, сохраняя проекционную связь.

Длина А₂ 1 В₂ 1 равна натуральной величине отрезка AB.

Вопросы для самопроверки.

1. В чём сущность преобразования проекций способом вращения?

2. В чем сущность преобразования проекций способом вращения вокруг оси, перпендикулярной плоскости?

3. В чём сущность способа преобразования проекций способом вращения вокруг горизонтали или фронтали?

4. Каковы основные принципы способа плоскопараллельного перемещения?

5. Как определить натуральную величину отрезка прямой способом плоскопараллельного перемещения?

7. Лекция 7. Кривые линии. Поверхности.

Общие положения. Классификация кривых линий.

Кривой линией называется геометрическое место (непрерывное множество) последовательных положений точки, движущейся в пространстве.

Кривые линии широко применяются в различных областях науки и техники, а также для образования поверхностей различных архитектурных деталей и конструкций, зданий и сооружений.

Кривые линии по положению точек в пространстве делятся на два вида:

1. Плоские кривые — это кривые, все точки которых лежат в одной плоскости; к ним относятся — окружность, парабола, гипербола, эллипс и т.д.

2. Пространственные кривые — это кривые, точки которых не лежат в одной плоскости. К ним относятся винтовые линии, линии пересечения двух кривых поверхностей и т.д.

Кривые линии подразделяются и по другим признакам. Кривая может быть описана аналитически, т.е. уравнением (алгебраическим или трансцендентным), например эллипс, парабола, синусоида и т.д. Если образование кривой не имеет строгой закономерности, то она задается графически, например, горизонтали на плане местности. Степень уравнения, которое выражает алгебраическую кривую, определяет порядок кривой. Геометрически порядок плоской кривой определяется числом ее точек пересечения прямой линией. Примером может служить эллипс, его уравнение — это аналитически;

следовательно, эллипс — кривая второго порядка. Порядок пространственной кривой определяется числом точек пересечения кривой с плоскостью.

Кривая т — кривая четвертого порядка (рис. 47).

Источник

Лекция 4. Способы преобразования ортогонального чертежа

4.1. Способ перемены плоскостей проекций

Чаще всего геометрические объекты расположены относительно плоскостей проекций в общем положении, и при решении задач для достижения поставленной цели необходимо выполнять много построений.

Количество построений можно значительно сократить, если геометрические элементы будут расположены в частном положении относительно плоскостей проекций.

Существуют два основных способа преобразования чертежа, при которых:

1. Объект остаётся неподвижным, при этом меняется аппарат проецирования;
2. Условия проецирования не меняются, но изменяется положение объекта в пространстве.

К первому способу относится способ перемены плоскостей проекций.

Ко второму – способ вращения (вращение вокруг линии уровня и вращение вокруг проецирующей прямой); способ плоскопараллельного перемещения.

Рассмотрим наиболее часто используемые способы при решении задач.

Способ перемены плоскостей проекций или способ введения дополнительных плоскостей проекций (ДПП) позволяет перейти от заданной системы плоскостей проекций к новой системе, более удобной для решения той или иной задачи.

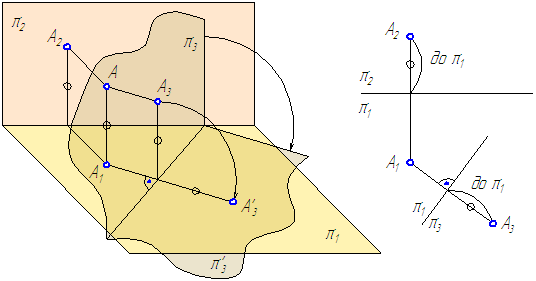
Рассмотрим положение точки А относительно известной системы плоскостей проекций π₂⊥π₁ (Рисунок 4.1, а и б).

Введём π₄⊥π₁, при этом получим новую систему двух взаимно перпендикулярных плоскостей. Положение точки А на эпюре будет в этом случае задано проекциями А₁ и А₄.

Правила перемены плоскостей проекций:

1. Новая плоскость проекций вводится перпендикулярно, по крайней мере, одной из заданных на чертеже плоскостей проекций;
2. ДПП располагается относительно проецируемого объекта в частном положении, удобном для решения поставленной задачи;
3. Новую плоскость совмещаем вращением вокруг новой оси проекций с плоскостью, которой она перпендикулярна на свободное место так, чтобы проекции не накладывались друг на друга.

а б

Рисунок 4.1 – Способ перемены плоскостей проекций

1. На чертеже новая проекция геометрического элемента находится на линии связи, перпендикулярной новой оси проекций:

1. Расстояние от А₄ до π₁/π₄ равно расстоянию от А₂ до π₂/π₁, так как величина этих отрезков (отмечены ○) определяет расстояние от точки А до плоскости проекций π₁.

При решении задачи необходимо заранее обдумать, как расположить новую плоскость проекций относительно заданных геометрических объектов (прямой, плоскости и др.), и как на чертеже провести новую ось проекций, чтобы в новой системе плоскостей заданные объекты заняли бы частные положения по отношению к новой плоскости проекций.

Упражнение

1. Спроецировать отрезок общего положения АВ в точку.

1. Введём ДПП π₄//А₁В₁ и π₄⊥π₁ (Рисунок 4.2). В новой системе двух взаимно перпендикулярных плоскостей проекций π₁/π₄ отрезок АВспроецируется на π₄ в натуральную величину и по этой проекции можем определить угол наклона отрезка к плоскости проекций π₁

Упражнение

2. Дана плоскость общего положения – σ, заданная треугольником АВС (Рисунок 4.3).

Определить истинную величину треугольника.

1. Введём ДПП π₄⊥σ и π₄⊥π₁, для чего построим горизонталь в плоскости треугольника и проведём новую ось проекций π₁/π₄⊥g₁согласно теореме о перпендикуляре к плоскости. На π₄ плоскость σ спроецируется в прямую, что означает σ⊥πp₄.
2. Введём ДПП π₅//σ (π₄/π₅//А₄В₄С₄) и π₄⊥π₅. На π₅ проекция А₅В₅С₅ – есть истинная величина треугольника.

4.2. Способ вращения

Сущность способа вращения состоит в том, что положение системы плоскостей проекций считается неизменным в пространстве, а положение проецируемого объекта относительно неподвижных плоскостей изменяется.

Из сравнения сущности обоих способов видно, что решение задач, которые требуют применения преобразования ортогонального чертежа, может быть выполнено любым из этих способов, результат при этом должен получиться одинаковым. Основа выбора того или иного способа – рациональность решения.

Вращение заданных элементов будем осуществлять вокруг проецирующей прямой, то есть прямой, перпендикулярной какой-либо плоскости проекций, при этом все точки заданных элементов поворачиваются в одну и ту же сторону на один и тот же угол (Рисунок 4.4, а и б). Ось вращения и объект вращения составляют твёрдое тело.

А – точка в пространстве;

О – центр вращения точки А;

АО – радиус вращения

а б

Рисунок 4.4 – Способ вращения вокруг прямой, перпендикулярной π₂

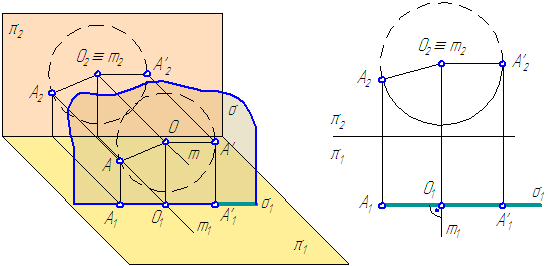
Точка описывает в пространстве окружность радиусом АО. Плоскость окружности перпендикулярна оси вращения (σ⊥m).

Так как m⊥π₂ , то σ//π₂, следовательно, σ⊥π₁, ⇒ σ₁⊥m₁, и поэтому σ проецируется на π₁ в виде прямой, перпендикулярной проекции оси вращения, а на π₂ траектория вращающейся точки проецируется в виде окружности с центром О₂≡m₂.

Пусть ось вращения m⊥π₁ (Рисунок 4.5, а и б). Плоскость окружности σ⊥m.

а б
Рисунок 4.5 – Вращение вокруг прямой, перпендикулярной π₁
\left.\begin\sigma\parallel\pi_1\\\sigma\perp \pi_2\\\end\right\> npu\;m\perp\pi_1\Longrightarrow\sigma_2\perp m_2
Свойства проекций

1. На плоскость проекций, перпендикулярную оси вращения, траектория вращающейся вокруг этой оси точки проецируется без искажения, то есть в окружность с центром, совпадающим с проекцией оси вращения на эту плоскость и радиусом, равным расстоянию от вращаемой точки до оси вращения.
2. На плоскость проекций, параллельную оси вращения, траектория вращающейся точки проецируется в отрезок, перпендикулярный проекции оси вращения на эту плоскость.
3. На плоскость проекций, перпендикулярную оси вращения, проекция вращаемого объекта своих размеров и формы не меняет.

Упражнение

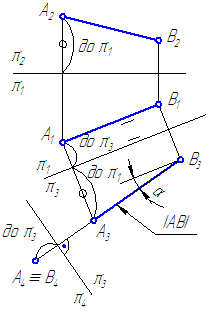
Дано : отрезок общего положения – АВ.

Определить : способом вращения истинную величину отрезка и углы наклона его к плоскостям проекций.

1. Выберем ось вращения m⊥π₁ и проходящую через точку В (Рисунок 4.6).

На плоскости проекций π₂ проекция траектории перемещения точки А – прямая,

A_2 \overline\perp m_2\;u\;A_2\overline\parallel\pi_2/\pi_1

На плоскости проекций π₁ проекция траектории перемещения точки А – окружность радиусом |А₁В₁|.

Повернем отрезок до положения, параллельного плоскости проекций π₂. Получим натуральную величину отрезка.

Угол наклона отрезка АВ к плоскости проекций π₁ будет угол
\alpha=\angle\widehat_2> .

Для того, чтобы определить угол наклона АВ к плоскости проекций π₂, надо ввести новую ось вращения перпендикулярно π₂ и повторить построения.

4.3. Определение истинной величины треугольника способом вращения

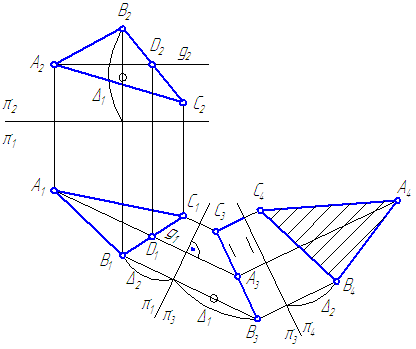
Пусть плоскость σ задана треугольником. Необходимо определить истинную величину треугольника (Рисунок 4.7).

Одним поворотом вокруг оси, перпендикулярной к плоскости проекций, истинную форму треугольника получить нельзя (так же как и введением одной ДПП).

Вращая вокруг оси m, перпендикулярной π₁ можно расположить плоскость ΔАВС⊥π₂ (а вращая вокруг оси n⊥π₂ можно расположить плоскость ΔАВС⊥π₁).

Рисунок 4.7

1. Положим σ’ должна быть перпендикулярна π₂. Для чего построим CD – горизонталь h плоскости σ. Введём первую ось вращения m⊥π₁, например, через точку С.
2. Повернём треугольник вокруг m до положения, когда
   \overline\perp\pi_2\Rightarrow\overline_1\overline_1\perp\pi_2/\pi_1
   На основании 3-го свойства, новая горизонтальная проекция треугольника \overline по величине должна равняться A₁B₁C₁, а фронтальная проекция треугольника будет представлять отрезок.
3. Введём вторую ось вращения n⊥π₂ через точку \overline_2 . Повернём фронтальную проекцию \overline в новое положение \overline<\overline\overline\overline>\parallel\pi_2/\pi_1 . На π₁ получим треугольник \overline<\overline\overline\overline> , равный истинной величине треугольника АВС.

4.4. Задачи для самостоятельной работы

Двумя способами преобразования ортогонального чертежа:

1. Определить расстояние от точки D до отрезка АВ – общего положения (Рисунок 4.8).

Рисунок 4.8

2. Определить расстояние между двумя параллельными прямыми общего положения (АВ//CD) (Рисунок 4.9).

Рисунок 4.9

3. Определить расстояние между двумя скрещивающимися прямыми, заданными отрезками АВ и CD (Рисунок 4.10).

Рисунок 4.10

4. Построить недостающую проекцию точки D при условии, что задана σ=ΔАВС – общего положения и первая проекция точки D₁, Dотстоит от плоскости σ на 30 мм (Рисунок 4.11).

Рисунок 4.11

5. Дан отрезок АВ – общего положения. Ось вращения не проходит через АВ (Рисунок 4.12). Определить способом вращения истинную величину АВ.

Рисунок 4.12

6. Задана прямая общего положения m и точка А вне прямой. Построить плоскость, проходящую через точку А и перпендикулярную прямой m (Рисунок 4.13).

Рисунок 4.13

Источник