Способ вращения плоскопараллельное перемещение

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
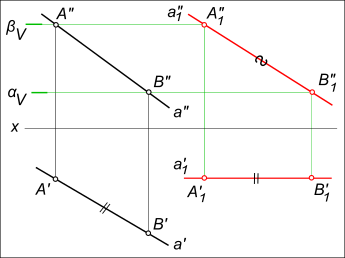
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»₁ и D»₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C»₁ и D»₁. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

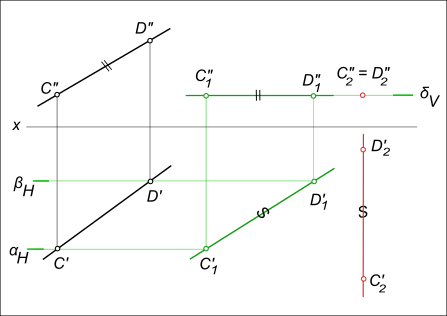
Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M»₁N»₁ = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M»₂ = N»₂ определяются по линиям связи.

Определение натуральной величины треугольника

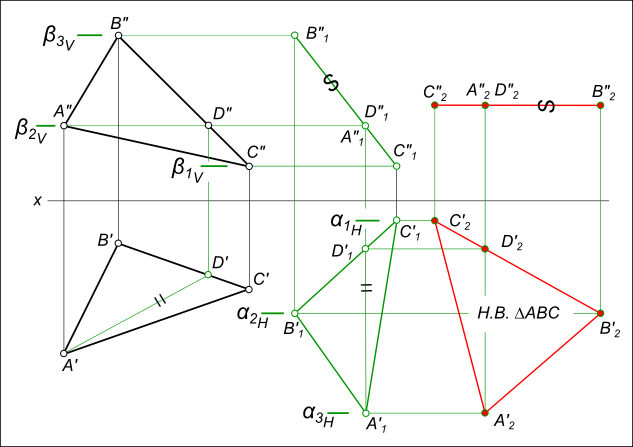
Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A»₁, B»₁, C»₁.
3. Перемещаем проекцию A»₁B»₁C»₁ треугольника ABC в положение A»₂B»₂C»₂, параллельное оси X, соблюдая равенство A»₂B»₂C»₂ = A»₁B»₁C»₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

Источник

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения (переноса) имеет справедливым утверждение, которое может быть выражено в виде следующей теоремы.

При параллельном переносе геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.

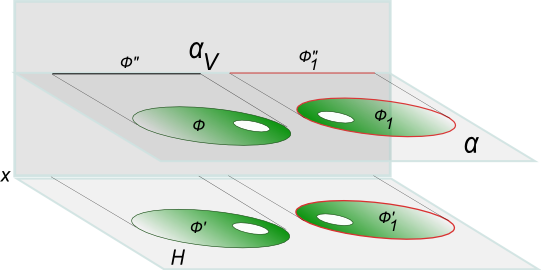
Докажем эту теорему для случая, когда проецируемая фигура Ф плоская, и ее плоскость принадлежит плоскости уровня Ф⊂α, плоскость α║H (рисунок). В этом случае, на основании свойства 6 ортогонального проецирования горизонтальная проекция Ф` будет конгруентна самой фигуре Ф(Ф`≅Ф).

При перемещении фигуры Ф в новое положение Ф₁, фигура Ф`₁ будет конгруентна Ф, так как:

а) расстояние между точками фигуры не меняется;

б) в процессе перемещения фигура Ф все время остается в плоскости α.

В силу параллельности плоскостей α и H, Ф`<sub>1</sub>≅Ф<sub>1</sub>, но Ф<sub>1</sub>≅Ф, а Ф≅Ф`, следовательно Ф`<sub>1</sub>≅Ф`. Данная теорема будет справедлива и в случае, когда геометрическая фигура занимает произвольное (непараллельное) положение относительно плоскости проекции.

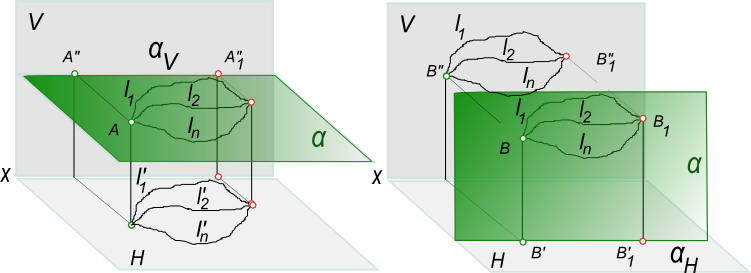
а) При всяком перемещении точки в плоскости, параллельной плоскости проекции H, ее фронтальная проекция перемещается по прямой, параллельной оси x.

б) В случае произвольного перемещения точки в плоскости, параллельной V, ее горизонтальная проекция перемещается по прямой, параллельной оси x.

Пользуясь теоремой и отмеченными свойствами, не составляет труда построить новые проекции геометрической фигуры (по заданным ее ортогональным проекциям), которые соответствуют частным положениям проецируемой фигуры по отношению к плоскости проекции.

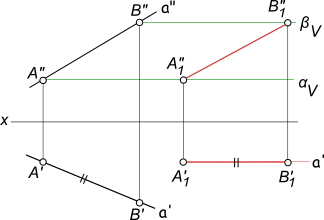
[AB]- отрезок прямой а общего положения перевести в положение параллельное V. Выполняем перемещение отрезка [A`B`] на горизонтальной плоскости проекции в положение параллельное оси x [A₁B₁]. При таком перемещении новая горизонтальная проекция конгруентна исходной [AB]≅[A₁B₁] на основании теоремы.

Фронтальные проекции точек отрезка [A»B»] будут перемещаться в новое положение [A»₁B»₁] в плоскостях α и β параллельных горизонтальной плоскости проекции — по следам α_V и β_V.

Для перевода отрезка прямой общего положения в положение параллельное V требуется одно перемещение отрезка параллельно плоскости проекции H.

Для перевода отрезка прямой из общего положения в проецирующее, необходимо последовательно выполнить два перемещения параллельно плоскостям проекции.

Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проецирующее, можно легко перевести плоскость, произвольно расположенную в пространстве, в частное положение (параллельное или перпендикулярное плоскости проекции).

В графической работе №4 используется способ плоскопараллельного перемещения для решение задачи по построению треугольной пирамиды SABC: Графическая работа 4. В графической работе №5 используется способ плоскопараллельного перемещения для решение задачи по по определению наклона ребра SC треугольной пирамиды SABC к плоскости основания ABC: Графическая работа 5. Плоскопараллельное перемещение треугольника, со всеми подробностями, смотри: Плоскопараллельное перемещение треугольника

Источник

Плоскопараллельное перемещение

Плоскопараллельное перемещение — способ перехода от общего положения геометрической фигуры к частному, которое можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости проекции путем перемещения в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве.

Данный путь лежит в основе метода плоскопараллельного перемещения

Плоскопараллельное перемещение осуществляется путем перемещения геометрической фигуры в новое положение так, чтобы траектория перемещения ее точек находились в параллельных плоскостях. Образно это можно представить в виде перемещения например отрезка вмерзшего в кусок льдины.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой траектории перемещения точек различают:

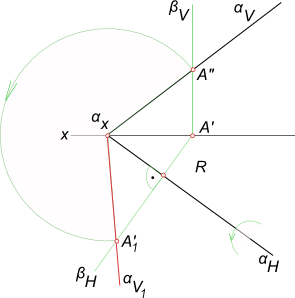
а) способ параллельного перемещения. Плоскости — носители траекторий перемещения точек параллельны какой-либо плоскости проекции. Траектория — произвольная линия.

б) способ вращения вокруг оси, перпендикулярной к плоскости проекций. Плоскости — носители траектории перемещения точек параллельны плоскости проекции. Траектория — дуга окружности, центр которой находится на оси,перпендикулярной плоскости проекции;

в) способ вращения вокруг оси, параллельной плоскости проекции (вращение вокруг линии уровня);

Плоскости — носители траектории перемещения точек перпендикулярны данной линии уровня. Траектория — дуга окружности, центр которой находится на линии уровня.

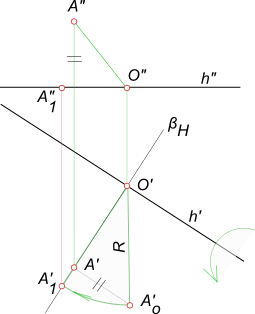
г) способ вращения вокруг оси, принадлежащей плоскости проекции (вращение вокруг следа плоскости);

Плоскости — носители траектории перемещения точек перпендикулярны данному следу плоскости. Траектория — дуга окружности, центр которой находится на следе плоскости.

Источник

Способ плоскопараллельного перемещения

Сущность способа плоскопараллельного перемещения состоит в том, что все точки геометрической фигуры перемещаются по произвольным траекториям в плоскостях уровня относительно плоскости проекций, вследствие чего сохраняется неизменным расстояние от точек геометрической фигуры до этой плоскости проекций.

На основании сказанного сформулируем основное свойство проекций данного способа. При плоскопараллельном перемещении соответствующая проекция геометрической фигуры не изменяет своей формы и размеров.

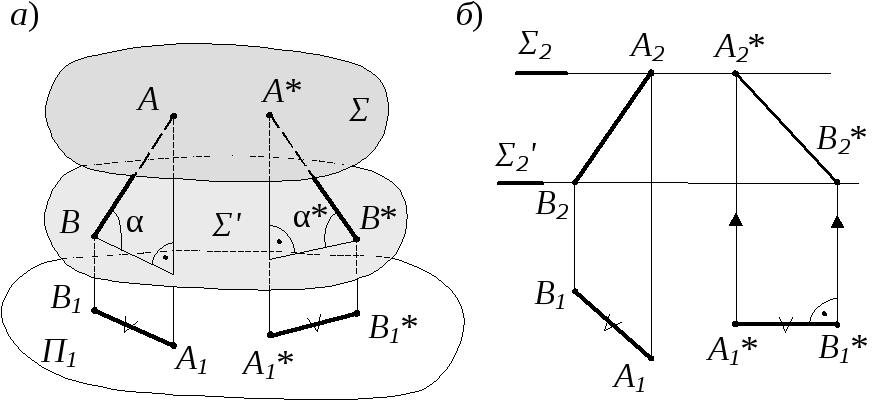
Докажем это свойство на примере перемещения прямой в плоскостях горизонтального уровня (рис. 30, а). ТочкиАиB,заданного отрезка прямой, перемещаются соответственно в плоскостяхΣиΣ‘,вследствие чего не изменяется разность расстояний от этих точек до горизонтальной плоскости проекций. Поэтому сохраняется неизменной величина угла наклона прямойАВк горизонтальной плоскости проекций, т. е. α = α*. Следовательно проекцииА₁В₁ и А₁ * В₁ * равны между собой.

На рис. 30, бпоказан пример преобразования на комплексном чертеже отрезка прямой (АВ) общего положения в прямую фронтального уровня, для чего перемещение заданного отрезка следует производить в плоскостях горизонтального уровня, так как при этом будет меняться только угол наклона отрезка прямой к фронтальной плоскости проекцийП₂. По условию задачи этот угол необходимо изменить от заданного в примере значения до нулевого, при котором прямая АВ будет параллельна плоскостиП₂.

На основании свойства проекций при плоско параллельном перемещении горизонтальную проекцию располагают в новом положении А₁ * В₁ * в любом удобном для построения месте и ориентируют перпендикулярно линиям связи, тем самым выполняя условие параллельности прямойАВи плоскостиП₂. Затем строят фронтальную проекциюА₂ * В₂ * .

Способ вращения

Сущность способа состоит во вращении геометрической фигуры вокруг прямолинейной оси в заданной системе плоскостей проекций.

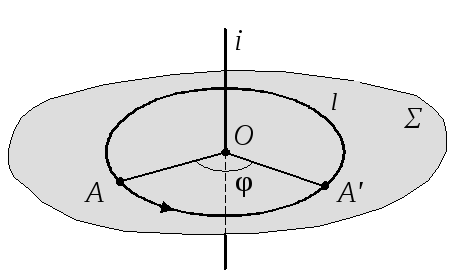
На рис. 31 показано вращение простейшей геометрической фигуры – точки (А) вокруг прямолинейной оси (i), где:

АО– радиус вращения;

l –траектория вращения – окружность;

φ – угол поворота точки вокруг оси.

Ось вращения (i)может занимать по отношению к плоскостям проекций следующие положения:

i –проецирующая прямая;

i– прямая уровня;

i – прямая общего положения.

В первом случае, когда ось перпендикулярна плоскости проекций, траектория вращения точки изображается в натуральную величину на соответствующую плоскость проекций, так как плоскость вращения является плоскостью уровня, а на другую в виде прямой, перпендикулярной линиям связи.

Во втором случае, когда ось вращения параллельна плоскости проекций, траектория вращения точки изображается на соответствующую плоскость проекций в виде прямой, так как плоскость вращения является проецирующей, а на другую в виде эллипса. Эта ситуация значительно усложняет графические построения на комплексном чертеже.

В третьем случае плоскость вращения точки является плоскостью общего положения, вследствие чего траектория вращения точки изображается на плоскостях проекций в виде эллипсов, что не позволяет выполнять на комплексном чертеже графические построения. Если по условию задачи необходимо выполнить вращение геометрической фигуры относительно прямой общего положения, то следует предварительно выполнить преобразование чертежа так, чтобы ось вращения стала прямой уровня или проецирующей, например, способом замены плоскостей проекций.

Источник