Способ вращения элемента вращения

Операция вращения

Операция вращения является второй по популярности формообразующей операцией КОМПАС-3D. В результате операции происходит перемещение эскиза вокруг выбранной оси. Операция вращения является частным случаем кинематической операции или элемент по траектории — название из последних версий КОМПАС.

Как сделать операцию вращения в КОМПАС

Для выполнения операции вращения необходим эскиз, в соответствии с которым и заданным углом вращения будет строиться операция.

Требования к эскизу операции вращения

Любая формообразующая операция базируется на эскизе. К эскизу есть определенные требования, которые зависят от типа операции. Для операции вращения справедливо:

• объекты, которые должны участвовать в операции, должны быть выполнены основной и осевой линиями. Контур выполняется основной линией, осевая линия обозначает ось вращения. Все вспомогательные линии выполняются любым другим стилем, в том числе и утолщенной линией;
• если эскиз содержит ось, то она не должна пересекать контур. Крайние точки контура могут лежать на оси, либо её продолжении;
• один замкнутый контур может быть вложен в другой замкнутый контур, степень вложенности любая.

Например, вот такой эскиз нельзя использовать для выполнения операции:

Контур пересекает ось, а это недопустимо

Такой эскиз в последних версиях применить можно, а вот в версиях ниже v17 КОМПАС бы «ругался» на пересечение контура. В версиях 17,18 будет выполнено вращение по объединенному контуру, т.е. окружность просто будет добавлена ко второй окружности.

Возможно применить и вот такой эскиз. В данном случае получится 2 тела

Вот такой эскиз также можно применить и получить цилиндр:

Для получения в точности такого же цилиндра можно применить и вот такой эскиз:

Одинаковый вариант будет получен при построении Сфероида, если же строить тонкостенную оболочку, то получим уже разные варианты. В первом случае:

А во втором случае:

Основное отличие эскиза для операции вращения от других типов операций — наличие осевой линии построенной командой «Отрезок» или соответствующими командами построения осевых, например, командой «Автоосевая».

Основные параметры операции вращения

Панель параметров при выполнении операции вращения объемная, но в большинстве случаев достаточно лишь части параметров, рассмотрим их подробнее.

Основной параметр — угол

Указываем нужное значение, а также пользуемся переключателем направления, если нужно выполнить вращение в другую сторону

Второй параметр, который часто приходится задавать — это выбор между объемным телом и тонкостенной оболочкой.

Если включить режим построения тонкой стенки, то появятся еще два параметра — Толщина 1 и Толщина 2, одна толщина внутрь, другая наружу.

Если вращение осуществляется не на 360 град., то важное значение имеют параметры: Симметрично и Второе направление.

Первый параметр позволяет задать одно значение угла, а построение будет вестись в обе стороны от эскиза. Второй параметр позволяет задать угол для второго направления.

К важным параметрам также следует отнести тип построения. Строить можно «Сфероид» или «Тороид».

При построении Сфероида крайние точки траектории будут проецироваться на ось симметрии. При построении Тороида в операции участвует только сам контур.

Пошаговая инструкция выполнения операции вращения.

Создаем эскиз, используя команду «Создать эскиз» . Способов вызова команды несколько. Чаще всего используют вызов с Панели быстрого доступа

Либо с контекстного меню, которое появляется при нажатии правой кнопкой мыши на плоскости или плоской грани

После запуска команды «Создать эскиз» система переходит в режим редактирования эскиза. В данном режиме необходимо выполнить построение контура, для упрощения выполним вращение эскиза в котором изображена окружность.

Построим окружность, воспользовавшись одноименной командой и отрезок со стилем линии осевая

В итоге получаем вот такой эскиз:

Длина оси не имеет никакого значения, главное чтобы в эскизе был объект со стилем линии Осевая.

Выполнив построения в эскизе можно сразу перейти к формообразующей операции. В нашем случае — это операция вращения:

Кликаем по команде «Элемент вращения» и вводим необходимые значения на Панели параметров. В нашем случае будем считать, что вращение необходимо на 360 градусов и тонкая стенка не нужна, поэтому ничего на Панели параметров задавать не нужно, все параметры оставляем умолчательными.

Подтверждаем операцию кнопкой «Создать объект» или нажав колесо на мышке. В итоге получаем следующее тело:

Вырезать вращением

Аналогично пошаговой инструкции добавления объема операцией вращения, можно производить удаление объема операцией вырезать вращением. Сама команда находится на инструментальной панели Элементы

Второй вариант выреза вращением- воспользоваться командой «Элемент вращения», но выбрать результат построения на Панели параметров «Вычитание»

Источник

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник

СПОСОБ ВРАЩЕНИЯ

Рассматриваемый способ вращения заключается в том, что положение геометриче­ских элементов относительно плоскостей про­екций изменяют вращением вокруг оси, которая проводится перпендикулярно к какой-нибудь плоскости проекций; положение плоскостей проекций при этом остается неизменным. На эпюре строят новые проекции повернутых гео­метрических элементов.

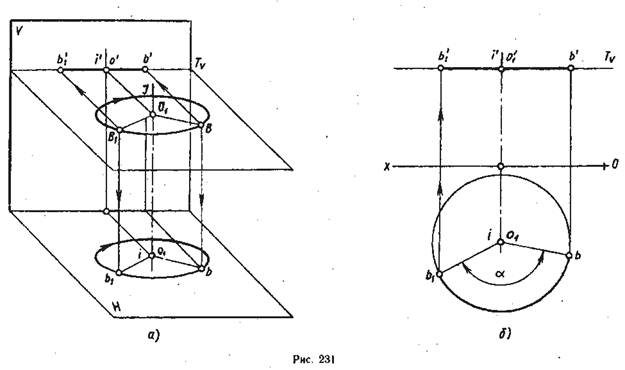
На рис. 231 показано вращение точки В во­круг оси I, перпендикулярной плоскости Н. Точку В вращают вокруг оси I (рис. 231, а) по окружности, радиус O₁В которой является перпендикуляром, опущенным из точки В на ось вращения I. Точка O₁ — центр вращения точки В. Точка В при вращении опишет дугу окружности, которая располагается в плоско­сти T, перпендикулярной оси вращения. А так как ось I перпендикулярна плоскости H, плос­кость Т будет горизонтальной плоскостью. Ось вращения — проецирующая прямая, перпен­дикулярная плоскости H. Траектория поворота точки В проецируется на плоскость Н окруж­ностью, а на плоскость V — отрезком прямой линии. Переместив горизонтальную проекцию точки В в новое положение b₁, т. е. повернув ее на заданный угол α, строят фронтальную проекцию, точки b׳₁ с помощью линии проекци­онной связи. Так как вращение происходит в плоскости Т, перпендикулярной плоскости V, фронтальная проекция b׳₁ точки В будет нахо­диться на следе T_v плоскости Т. Плоскость вращения на эпюре обычно не проводят.

Траектория вращения точки проецируется в дугу окружности на плоскость проекций, кото­рой перпендикулярна ось вращения. На плос­кость, которой ось вращения параллельна, траектория вращения точки проецируется в от­резок, параллельный оси проекций.

При определении натуральной длины отрез­ка для упрощения построений ось вращения проводят через конец отрезка.

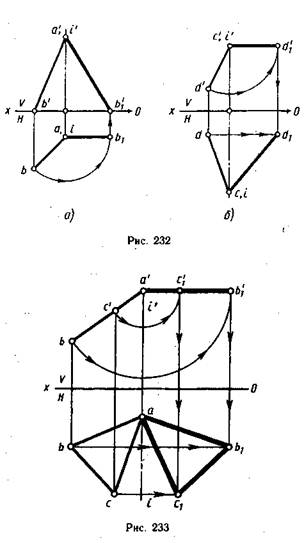
На рис. 232, а ось вращения I проведена через точку А перпендикулярно плоскости Н. При вращении точка В отрезка АВ описала дугу окружности с центром в точке, которая проецируется на плоскость Н в точку а, в эту же точку проеци­руется ось I(i).

Траектория точки В на плос­кость Н спроецировалась без искажения, а ее фронтальная проекция совпала с осью Ох. так как точка В лежит в плоскости Н.

Движение точки В остановлено в тот момент, когда го­ризонтальная проекция ab отрезка АВ стала параллельной оси Ох. Отрезок расположился параллельно плоскости V и проецируется на нее в натуральную величину.

На рис. 232, б ось вращения проведена пер­пендикулярно плоскости V через точку С. Ее фронтальная проекция совпала с фронтальной проекцией с’ точки С и проекцией оси враще­ния I (i‘) точки D. Фронтальная проекция c’d׳ отрезка CD повернута до положения, параллельного оси Ох. Отрезок стал парал­лельным плоскости Н и спроецировался на нее в натуральную величину. Траектория точки D при вращении проецируется на плоскость И отрезком dd\_y параллельным оси Ох.

На рис. 233 показан поворот треугольника ABC (плоскость треугольника ABC перпендику­лярна плоскости V) в положение, параллельное плоскости H. Для этого через одну из вершин треугольника (А) проводят ось вращения перпендикулярно плоскости V. Отрезок а’b’ — про­екцию треугольника ABC на плоскость V — поворачивают в положение, параллельное оси Ох. Траектории поворота вершин треуголь­ника спроецировались на плоскость V в дуги окружностей, а на плоскость H — в отрезки прямых, параллельных оси Ох. Проведя линии проекционной связи из точек с׳₁ и b׳₁ до пересече­ния с этими отрезками, получают проекцию ab₁c₁ треугольника после поворота. Точка А своего положения не изменила, так как она находится на оси вращения. На плоскость H треугольник спроецировался в натуральную величину, так как его плоскость параллельна плоскости H.

Способ вращения без указания осей или способ плоскопараллельного пе­ремещения может быть применен в тех же случаях, что и рассмотренный выше способ вращения. Если на плоскости V на свободном месте чертежа изобразить фронтальную проек­цию c’d’ прямой CD (рис. 234, а) в новом по­ложении, где проекция c׳₁d׳₁ будет параллельна оси Ох, то, очевидно, существует такая ось вращения, поворот вокруг которой привел пря­мую CD именно в такое положение. Ось вра­щения можно не указывать, так как все пост­роения могут быть проделаны без нее. На го­ризонтальной плоскости проекций траектории перемещения совпадут с прямыми, параллель­ными оси Ох. Опустив из точек с׳₁ и d׳₁ линии связи до пересечения с этими прямыми, полу­чим проекцию с₁d₁ прямой CD, которая в но­вом положении проецируется на плоскость Н в натуральную величину.

На рис. 234, б без указания оси вращения по­казан поворот треугольника ABC в положение, параллельное плоскости Н. Его фронтальная проекция а׳₁b’₁с׳₁ изображена на произвольном месте плоскости V параллельно оси Ох.

Из сказанного следует, что проекции гео­метрических элементов при вращении не изме­няют своей величины на той плоскости проек­ций, которой перпендикулярна ось вращения. Это происходит потому, что угол наклона пря­мой или плоскости к плоскости проекций, к которой перпендикулярна ось, не изменяется при перемещении этих геометрических элемен­тов. Взаимное расположение точек при поворо­те, а значит, форма и величина проекции вращаемого объекта на этой плоскости проек­ций остаются без изменений. Меняется лишь ее положение.

На этом и основан способ вращения без ука­зания осей. Одну из проекций вычерчивают в новом положении по отношению к оси проек­ций Qx, а на другой плоскости проекций про­водят прямые, параллельные оси Ох, изобра­жающие на плоскости проекций путь переме­щения точек. В пересечении линий проекцион­ной связи, проведенных от проекций точек после поворота, и линий, параллельных оси Ох, получают точки, определяющие положение второй проекции после поворота.

Источник