Способ вращения для преобразования чертежа

Способы преобразования чертежа

Способы преобразования чертежа служат для решения метрических задач по определению натуральной величины геометрических объектов (отрезка прямой или плоскости), либо кратчайшего расстояния между геометрическими объектами.

Суть этих способов заключается в том, что необходимо преобразовать комплексный чертеж так, чтобы рассматриваемый геометрический объект занял положение параллельное какой-либо плоскости проекций. Тогда на нее он, очевидно, спроецируется в натуральную величину.

Такое преобразование комплексного чертежа может быть осуществлено двумя основными способами:

1. Способом вращения, при котором оставляют неизменной систему плоскостей проекций, а меняют положение заданного геометрического объекта путем его вращения вокруг одной или последовательно вокруг двух подходящим образом выбранных осей так, чтобы интересующие нас прямые или плоскости оказались параллельными одной из плоскостей проекций. В качестве оси вращения обычно выбирают прямую, перпендикулярную одной из плоскостей проекций.

2. Способом замены плоскостей проекций, при котором оставляют неизменным положение в пространстве геометрического объекта, а заменяют одну или последовательно обе плоскости проекций так, чтобы интересующие нас прямые или плоскости оказались параллельными одной из новых плоскостей проекций.

Этими способами также можно решать задачи на приведение геометрических объектов в проецирующее положение.

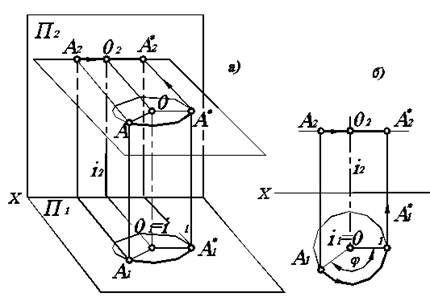
Способ вращения вокруг проецирующей оси

Рассмотрим вращение точки А вокруг оси i, перпендикулярной горизонтальной плоскости проекций П₁ (рис. 4.1). Ось вращения проецируется на плоскость П₁ в точку, а на плоскость П₂ — в прямую, перпендикулярную оси ОХ. Траекторией движения точки А будет окружность, лежащая в плоскости вращения, параллельной плоскости П₁, с центром вращения в точке О, лежащей на оси, и с радиусом вращения ОА (рис. 4.1, а).

Траектория движения точки проецируется на плоскость П₁ в натуральную величину, а на плоскость П₂ — в виде прямой, параллельной оси ОХ. Радиус окружности проецируется на плоскость П₁ в натуральную величину. Таким образом, горизонтальная проекция А₁ точки А движется по окружности, а фронтальная проекция А₂ — по прямой, параллельной оси ОХ.

Для того, чтобы повернуть точку А на угол j, откладывают этот угол на горизонтальной проекции (рис. 4.1, б) и получают горизонтальную проекцию А₁ точки А в новом положении А₁*. Фронтальную проекцию А₂* этой точки находят с помощью линии проекционной связи, которую проводят из точки А₁* до пересечения с прямой, проведенной из точки А₂ параллельно оси ОХ.

Рис. 4.1. Вращение точки вокруг горизонтально-проецирующей оси

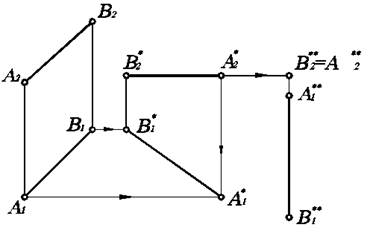
Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения является частным случаем способа вращения вокруг проецирующей оси, с той лишь разницей, что геометрический объект можно не только вращать, но и перемещать вдоль плоскости, параллельной одной из плоскостей проекций.

При перемещении отрезка прямой в новое положение таким образом, что его крайние точки движутся параллельно какой-либо плоскости проекций, длина проекции отрезка на эту плоскость остается неизменной (рис. 4.2).

Рис. 4.2. Плоскопараллельное перемещение отрезка прямой.

Преобразуем последовательно отрезок прямой линии общего положения АВ в положение горизонтали, затем фронтально-проецирующее положение. Для этого расположим фронтальную проекцию А₂В₂ отрезка АВ параллельно оси ОХ (А₂*В₂* параллелен ОХ) в любом месте чертежа. При этом точки А₁ и В₁ перемещаются в новое положение по прямым, параллельным оси ОХ, и будут лежать на линиях связи с А₂*, В₂* соответственно.

Тогда новая горизонтальная проекция займет положение А₁*В₁*. Очевидно, что А₁*В₁*- натуральная величина отрезка АВ, т.к. А*В* является горизонталью. Затем А₁*В₁* переместим в новое положение, чтобы А₁**В₁** была перпендикулярна оси ОХ. Тогда А₂** = В₂**, т.е. АВ займет положение проецирующей прямой. Следует заметить, что при определение натуральной величины АВ, которой является А₁*В₁*, удаленность проекции А₂*В₂* от оси ОХ не играет роли. Важно лишь выполнение двух требований: А₂*В₂* должна быть равна А₂В₂ и параллельна оси ОХ.

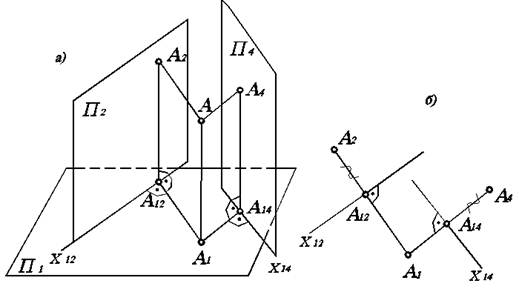
Способ замены плоскостей проекций

Способ замены плоскостей проекций состоит в том, что одна из основных плоскостей проекций П₁ или П₂ заменяется новой плоскостью проекций П₄, подходящим образом расположенной относительно изображаемого геометрического объекта, но перпендикулярной незаменяемой плоскости проекций.

В результате замены одной из основных плоскостей на плоскость проекций П₄ получаем вместо старой системы плоскостей проекций П₁/П₂ новую систему П₁/П₄ (рис. 4.3), если заменялась плоскость П₂, и систему П₂/П₄, если заменялась плоскость П₁.

Рис. 4.3. Интерпретация способа замены плоскостей проекций

Например, на рис. 4.3а плоскость П₄ может выступать в роли фронтальной плоскости проекций П₂. На рисунке 4.3б, фигурными скобками отмечены расстояния от точки А до горизонтальной плоскости проекций П₁. Естественно, как видно на рис. 4.3а, эти расстояния равны А₂А₁₂ = А₄А₁₄, так как высота точки А над плоскостью П₁ проецируется как на П₂, так и на П₄ в виде одинаковых отрезков. Расстояние же до П₂ и П₄ от точки А могут быть различными, поэтому А₁А₁₂¹А₁А₁₄.

Способ замены плоскостей проекций рационально применять при решении следующих задач:

— определение натуральной величины отрезка прямой линии;

— определение натуральной величины плоской фигуры;

— определение натуральной величины двугранного угла;

— определение кратчайшего расстояния от точки до прямой линии или до плоскости;

— определение кратчайшего расстояния между двумя параллельными или двумя скрещивающимися прямыми.

Решение задач данным способом рассмотрим на нескольких примерах.

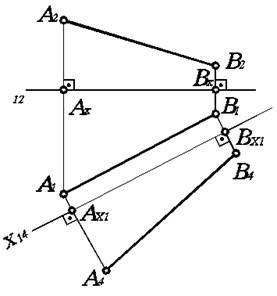
Определение длины отрезка общего положения

Для определения натуральной величины (длины) отрезка АВ прямой линии необходимо сделать этот отрезок прямой линии общего положения в новой системе плоскостей проекций линией уровня. Чтобы отрезок АВ стал линией уровня относительно новой плоскости проекций, заменим плоскость П₂ на плоскость П₄, параллельную АВ, и перейдем от системы П₁/П₂ к системе П₁/П₄. Новую ось проекций X₁₄, выбираем параллельно А₁В₁ (рис. 4.4). Для построения новой проекции отрезка АВ проводим новые линии проекционной связи перпендикулярно оси Х₁₄, и отмечаем на них новые проекции А₄, В₄ точек А и В. Для этого откладываем А_х1А₄ = А₂А_х, В_х1В₄ = В₂В_х.

Рис. 4.4. Преобразование прямой общего положения в прямую уровня.

Соединяя найденные точки А₄, В₄, получаем новую проекцию А₄В₄ отрезка АВ. Как видим, отрезок АВ в новой системе плоскостей проекций П₁/П₄ является линией уровня, так как А₁В₁ параллельна X₁₄, а следовательно, АВ параллельна П₄. Тогда, очевидно, что А₄В₄ является натуральной величиной отрезка АВ.

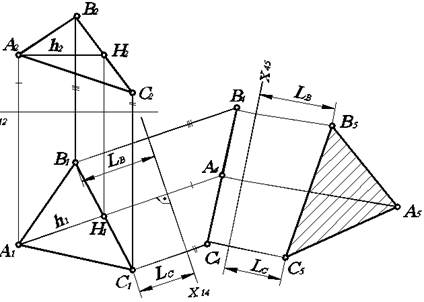
Определение натуральной величины плоской фигуры

Для определения натуральной величины плоской фигуры необходимо дополнительную плоскость построить так, чтобы она была параллельна рассматриваемой фигуре, и тогда на эту плоскость проекций плоская фигура спроецируется в натуральную величину. Если в качестве плоской фигуры выбрать треугольник, тогда задача формулируется следующим образом: преобразовать плоскость треугольника общего положения в новой системе плоскостей проекций в плоскость уровня.

Одной заменой плоскостей проекций эту задачу решить невозможно, так как необходимо соблюдать условие: новая плоскость должна быть перпендикулярна незаменяемой. Поэтому решим эту задачу двумя заменами: первой заменой введем плоскость, которая перпендикулярна треугольнику АВС, второй заменой – плоскость, параллельную треугольнику АВС.

Для того, чтобы построить плоскость П₄, перпендикулярную треугольнику АВС, необходимо расположить ее так, чтобы она была перпендикулярна фронтали либо горизонтали треугольника АВС.

Пусть П₄ перпендикулярна горизонтали, тогда новая ось Х₁₄ должна быть перпендикулярна h₁ (рис. 4.5).

Рис. 4.5. Преобразование плоскости общего положения в плоскость уровня.

Построим ее на произвольном расстоянии от треугольника А₁В₁С₁. Затем из точек А₁, В₁, С₁ проведем линии связи перпендикулярно Х₁₄. На каждой из них от оси Х₁₄ отложим отрезок, равный расстоянию от фронтальной проекции соответствующей точки до оси Х₁₂. В результате получаем новую проекцию В₄А₄С₄ треугольника АВС, которая представляет собой прямую, поскольку плоскость треугольника АВС перпендикулярна плоскости П₄.

Второй заменой вводим вместо П₁ плоскость П₅, параллельную плоскости треугольника АВС. Тогда получается система плоскостей проекций П₄/П₅, ось Х₄₅ которой параллельна В₄А₄С₄. Она может быть расположена на произвольном расстоянии от В₄А₄С₄. Далее из точек В₄ А₄ С₄ проводим линии связи перпендикулярно Х₄₅, и на каждой из них от оси Х₄₅ откладываем отрезок, равный расстоянию от горизонтальной проекции соответствующей точки до оси Х₁₄. Получим точки А₅, В₅, С₅, соединив которые имеем треугольник А₅В₅С₅, который и является натуральной величиной треугольника АВС, поскольку в новой системе плоскостей проекций треугольник АВС параллелен плоскости П₅.

Вопросы для самоконтроля

1. С какой целью осуществляется преобразование комплексного чертежа?

2. В чем заключается способ вращения вокруг проецирующей оси?

3. Назовите основные способы преобразования комплексного чертежа?

4. В чем сущность способа плоскопараллельного перемещения.

5. В чем заключается способ замены плоскостей проекций?

Источник

Способ вращения для преобразования чертежа

На чертежах некоторые элементы изображаются в искаженном виде. В некоторых случаях требуется определить действительную величину этих элементов, например, при выполнении чертежей разверток поверхностей геометрических тел.

Изучая прямоугольное проецирование отрезков прямых или плоских кривых линий, а также фигур (треугольника, круга и др.) на три плоскости V, H и W, можно отметить, что действительные размеры и виды этих линий и фигур получаются на той плоскости проекций, параллельно которой расположены эти линии и фигуры (рис. 117). Например, отрезок прямой А В, параллельный плоскости V (отрезок фронтали), проецируется в действительную длину на плоскость V или, иначе, длина фронтальной проекции a’в’ отрезка фронтали равна действительной длине этого отрезка.

Если плоскость фигуры, например треугольника АВС, параллельна фронтальной плоскости проекций, то фронтальная проекция а’b’с’ является его действительным видом.

В техническом черчении иногда приходится по данным прямоугольным проекциям (комплексному чертежу) детали определять действительную величину или вид какого-либо элемента этой детали, расположенного в плоскости общего положения. Для этого применяются особые способы построения, цель которых получить новую проекцию элемента детали, представляющую собой его действительную величину или вид.

Такими способами являются: способ вращения, способ совмещения (частный случай предыдущего способа) и способ перемены плоскостей проекций.

СПОСОБ ВРАЩЕНИЯ

Сущность способа вращения заключается в том, что заданные точка, линия или плоская фигура вращаются вокруг оси, перпендикулярной к одной из плоскостей проекций, до требуемого положения относительно какой-либо плоскости проекций. Если вращается фигура или тело, то каждая их точка будет перемещаться по окружности.

Рассмотрим вращение простейшего геометрического элемента — точки А (рис. 118, а). Пусть ось вращения MN будет перпендикулярна к плоскости . При вращении вокруг оси MN точка А перемещается по окружности, лежащей в плоскости, перпендикулярной к оси вращения. Точка пересечения этой плоскости с осью называется центром вращения.

Так как окружность, по которой движется точка А, расположена в плоскости, параллельной плоскости Н, то горизонтальная проекция этой окружности является ее действительным видом, а фронтальная проекция — отрезком прямой, параллельной оси х. Длина этого отрезка равна диаметру окружности, лежащей в плоскости вращения.

Таким образом, при вращении точки А вокруг оси, перпендикулярной к какой либо плоскости проекций, проекция точки на эту плоскость перемещается по окружности, а вторая проекция — по прямой, параллельной оси проекций.

Повернем данную точку А вокруг оси , перпендикулярной к плоскости V, на заданный угол а. Для этого на комплексном чертеже необходимо выполнить следующие построения (рис. 118, б).

Фронтальную проекцию оси вращения — точку m’n’ — соединяют прямой линией с фронтальной проекцией а’ точки А и получают отрезок m’a’, равный действительной величине (длине) радиуса окружности вращения. Этим радиусом из центра m’ описывают дугу окружности вращения (рис. 118, На плоскости V строят угол а, одна сторона которого является радиусом вращения а’m’. На пересечении дуги окружности вращения с другой стороной угла а получаем точку а’₁ — новую фронтальную проекцию точки Новую горизонтальную проекцию точки А находят, проводя вертикальную линию связи из точки а’₁ до пересечения с прямой, проведенной из точки а параллельно оси х.

Вращение отрезка прямой вокруг оси, перпендикулярной к плоскости проекций, можно рассматривать как вращение двух точек этого отрезка.

Построения на комплексном чертеже упрощаются, если ось вращения провести через какую-либо конечную точку вращаемого отрезка прямой. В этом случае достаточно повернуть только одну точку отрезка, так как другая точка, расположенная на оси вращения, остается неподвижной.

Пусть требуется определить способом вращения действительную длину отрезка прямой общего положения (рис. 119, а).

Через конец отрезка А (рис. 119, б) проводят ось вращения MN перпендикулярно плоскости Н. Относительно этой оси вращается второй конец отрезка — точка В. Чтобы получить на комплексном чертеже действительную длину отрезка, надо повернуть его так, чтобы он был параллелен плоскости V.

После вращения горизонтальная проекция отрезка должна быть параллельна оси х, поэтому на этой плоскости проекций и начинается построение. Из точки а радиусом ab описывают дугу окружности до пересечения с прямой, проведенной из точки а параллельно оси х (рис. 119, б). Точка пересечения b₁ — новая горизонтальная проекция точки В. Фронтальную проекцию b’₁ точки В находят, проводя вертикальную линию связи из точки b₁ до пересечения с прямой, проведенной из точки b’ параллельно оси х (в данном случае эта прямая совпадает с осью х). Соединив точки b’₁ и а’, на плоскости V получают действительную длину а’b’₁ отрезка AВ.

Эту задачу можно решить вращением отрезка А В относительно оси, перпендикулярной к плоскости V. Через конец отрезка А проводят оси вращения MN (рис. 119, в). Из точки а’ радиусом, равным a’b’ проводят дугу окружности до пересечения с прямой, проведенной из точки а’ параллельно оси х, и получают новую фронтальную проекцию b’₁ точки В. Проведя из точки b прямую, параллельную оси х, а через точку b’₁ вертикальную линию связи, на их пересечении получают новую горизонтальную проекцию b₁ точки В (после поворота отрезка АВ). Соединив точки b₁ и a, находят действительную длину ab₁ отрезка АВ.

Способом вращения можно определить действительный вид фигуры. На рис. 120, а изображена стойка поддерживающего ролика ленточного конвейера. Пусть требуется определить действительный вид ребра стойки ролика — прямоугольного треугольника АВС.

Как видно из рис. 120, плоскость треугольника горизонтально-проецирующая, поэтому действительный вид треугольника можно получить на плоскости V вращением этого треугольника около вертикальной оси до тех пор, пока плоскость треугольника не станет параллельной плоскости V.

На комплексном чертеже (рис. 120 б) ось вращения, перпендикулярная к плоскости H, проведена через вершину треугольника А. Вращаются одновременно две вершины треугольника — В и С. После поворота новая горизонтальная проекция треугольника a₁b₁c₁ должна быть параллельна оси х. Фронтальные проекции — точки b’₁ и c’₁ — вершин В и С после поворота находят, проводя вертикальные линии связи из точек с₁ и b₁. Соединив точки а’, b’₁и c’₁, получим на плоскости V действительный вид треугольника АВС.

Способом вращения на комплексном чертеже можно найти действительный вид фигуры криволинейного контура, например, лопасти мешалки (рис. 121, б). На рис. 121, а дано наглядное изображение одной лопасти этой мешалки и части вала. Так как лопасть расположена под углом к оси вала, на котором она установлена, а ось вала на комплексном чертеже должна быть параллельна оси х, то на фронтальной и профильной проекциях лопасть будет изображена в искаженном виде.

Действительный вид контура лопасти находят вращением лопасти вокруг оси, перпендикулярной к плоскости Н. Для этого на фронтальной проекции контура берут несколько произвольных точек— a’, е’, m’,d’,c’, к’, n’ (рис. 122). Проводя из этих точек вертикальные линии связи, находят их горизонтальные проекции — a, е m,d,c, к, n, которые будут располагаться на горизонтальной проекции контура лопасти, т. е. на прямой ав, наклоненной под углом а к оси x. Вертикальная ось вращения проведена через точку А. Горизонтальную проекцию аb контура лопасти поворачивают вокруг центра вращения (точки a) на угол а и получают новую горизонтальную проекцию ab₁ лопасти.

Для определения новой фронтальной проекции какой-либо точки контура, например точки b’₁ через точку b₁ проводят вертикальную линию связи до пересечения с прямой, проведенной из b’ параллельно оси x. Также находят и остальные новые фронтальные проекции точек контура — е’₁, m’₁,d’₁,c’₁, к’₁, n’₁ . Соединяя их плавной кривой по лекалу, получим действительный вид контура лопасти.

СПОСОБ СОВМЕЩЕНИЯ

Сущность способа совмещения заключается в том, что плоскость, заданную следами, вращают вокруг одного из следов этой плоскости до совмещения с соответствующей плоскостью проекций, например, вокруг следа Рн до совмещения с горизонтальной плоскостью проекций (рис. 123, а). Изображения отрезка прямой или плоской фигуры, лежащей в заданной плоскости Р, получаются без искажения.

Построения на комплексном чертеже упрощаются, если через совмещаемые геометрические элементы можно провести какую-либо проецирующую плоскость, например горизонтально-проецирующую. При любом расположении горизонтально-проецирующей плоскости Р относительно V и H ее следы после совмещения будут располагаться под прямым углом (рис. 123, а и б). Совмещая горизонтально-проецирующую плоскость с плоскостью Н вращением около горизонтального следа Рн, видим, что совмещенный фронтальный след Р_v1 находится под прямым углом к неподвижному горизонтальному следу Рн (рис. 123, б).

Если на горизонтальном следе Рн, который является осью вращения горизонталъно-проецирующей плоскости Р и, следовательно, неподвижен, взять какую-либо точку, то после совмещения плоскости с плоскостью Н положение точки не изменится.

Если же взять точку В на фронтальном следе Р_v плоскости Р (рис. 123, в), то совмещенная точка В будет лежать на совмещенном следе P_v1 при этом расстояние Р_Хb’ будет равно расстоянию Р_Хb’₁.

Отрезок прямой определяется двумя точками. Поэтому, если через отрезок AB провести, например, фронтально-проецирующую плоскость Р (рис. 124, а) и совместить ее с Н,то при этом с плоскостью Н совместятся и концы этого отрезка — точки A и B т. е. весь отрезок прямой. Тогда на плоскости Н отрезок спроецируется без искажения.

Таким образом, задача определения действительной длины отрезка прямой АВ способом совмещения решается следующим путем.

Через точку а (рис. 124, а), расположенную на плоскости H, проводят перпендикулярно оси горизонтальный след Р_н фронтально-проецирующей плоскости Р.Через точки а’ и b’ проводят след Р_v. Плоскость Р совмещают с плоскостью Н, совмещенное положение следа P_v совпадает с осью х. Из точки Р_х радиусом делают засечку дугой окружности на совмещенном следе Р_v1 и из точки пересечения восставляют перпендикуляр к оси х. Из точки b опускают перпендикуляр на след R_H и, продолжая его до пересечения с прямой, перпендикулярной к оси х , получают совмещенное положение точки В — точку b’₁. Соединив точки a’₁ и b’₁ находят совмещенное положение отрезка которое и будет его действительной длиной.

Определение действительного вида треугольника АВС показано на рис. 124, б. Как и при решении задачи способом вращения, здесь рассматривается случай, когда плоскость треугольника является горизонтально проецирующей.

Решая эту задачу способом совмещения, вначале проводят следы Р_v и Р_н плоскости треугольника АВС. Так как сторона АС треугольника расположена в плоскости. параллельной Н, то проекция ас совпадает со следом Р_н.Затем совмещают с плоскостью Н фронтальный след плоскости P_v, который после совмещения будет располагаться под углом 90° к горизонтальному следу Р_н.

Для построения совмещенного положения точки В из точки b’ проводят прямую, параллельную оси до пересечения со следом P_v в точке v’; на совмещенном следе P_v1 делают засечку дугой окружности радиусом, равным P_xv’ и получают точку v₁ — совмещенное положение точки V. Через точку v₁ проводят прямую, параллельную следу Р_н. Совмещенное положение точки В находится в точке b’₁ пересечения перпендикуляра, восставленного из точки b к следу Р_н с прямой, проведенной из точки параллельно следу P_н .

Определение действительного вида фигуры криволинейного контура, например лопасти мешалки, способом совмещения показано на рис. 125. Построение аналогично описанному выше. Различие состоит в том, что в данном случае совмещают несколько произвольно взятых точек криволинейного контура.

Через фигуру (контур) лопасти проводят вспомогательную горизонтально-проецирующую плоскость, заданную следами P_v и Р_н. Затем на криволинейном контуре берут несколько произвольно расположенных точек А, В, С, . через которые проводят горизонтали этой плоскости. Плоскость Р совмещают с плоскостью Н вместе с горизонталями. На совмещенных горизонталях находят точки a’₁, b’₁,c’₁, которые соединяют плавной кривой, и получают действительный вид контура лопасти.

Например, для совмещения с плоскостью Н точки В криволинейного контура через точку В проводят горизонталь плоскости Р. Фронтальная проекция горизонтали параллельна оси х; горизонтальная проекция горизонтали совпадает с горизонтальным следом Р_н. Затем эту горизонталь совмещают с плоскостью Н. Совмещение произведено таким образом. Фронтальная проекция горизонтали пересекает фронтальный след Р_v плоскости Р в точке v’, которая является фронтальным следом горизонтали. Совмещенное положение этого следа находится на совмещенном фронтальном следе Р_v в точке v₁ Из точки v₁ проведена прямая, параллельная Р_v, которая и будет совмещенным положением горизонтали, проходящей через точку В.

Из горизонтальной проекции b’₁ точки восставлен перпендикуляр к Р_н и продолжен далее до пересечения с совмещенной горизонталью в точке b’₁. Эта точка и будет являться искомым совмещенным положением точки В с плоскостью Н.

СПОСОБ ПЕРЕМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Сущность способа перемены плоскостей проекций заключается в том, что одна из плоскостей проекций заменяется новой, на которую проецируются данная точка, отрезок прямой линии или фигура. При этом в отличие от двух предыдущих способов эти геометрические элементы не меняют своего положения в пространстве. Например, фронтальная плоскость проекций V может быть заменена новой, обозначаемой (рис. 126, а), причем плоскость V₁ должна быть так же, как и плоскость V, перпендикулярна к плоскости H.

На комплексном чертеже (рис. 126, б) новая ось проекций, которая образуется при пересечении новой плоскости V₁ с плоскостью обозначается x₁. Новая система плоскостей проекций обозначается V₁/H. Иногда заменяется и горизонтальная плоскость проекций Н на новую плоскость, обозначаемую H₁. Если новая фронтальная плоскость проекций по своему положению являлась, как и замененная V, вертикальной плоскостью, то новая горизонтальная плоскость проекций Н₁ по своему положению не будет горизонтальной, а называется так только условно.

В некоторых случаях для решения задач на комплексном чертеже приходится последовательно заменять две плоскости проекций, например, фронтальную V на V₁ и горизонтальную Н на Н₁ наглядном изображении проекций точки А (рис. 126, а) видно, что при перемене фронтальной плоскости проекций V на новую V₁ расстояние от новой фронтальной проекции а’₁ точки А до новой оси проекций х₁ равно расстоянию от фронтальной проекции а’ точки А до оси проекции x, т. е. координате z_A. Это правило надо запомнить. В дальнейшем оно применяется при решении разных задач способом перемены плоскостей проекций.

Таким образом, при замене плоскости V на плоскость V₁ на комплексном чертеже прежде всего должна быть проведена новая ось проекций x₁ (рис. 126, а), а затем построена новая фронтальная проекция точки. Для этого из горизонтальной проекции а точки А опускают перпендикуляр на новую ось проекций х₁ и на продолжении этого перпендикуляра откладывают от новой оси координату z_A. В результате получают новую фронтальную проекцию а’₁ точки А.

Если на комплексном чертеже точки А нужно заменить горизонтальную плоскость проекций, то для нахождения новой горизонтальной проекции a₁ точки А надо (рис. 127, а и б) из фронтальной проекции а’ опустить на новую ось х₁ перпендикуляр и на его продолжении отложить координату у_А точки А.

Определим способом перемены плоскостей проекций действительную длину отрезка AB (рис. 128). В этом случае новая плоскость проекций V₁, или Н₁ должна быть выбрана так, чтобы она была параллельна отрезку АВ. Иначе отрезок AВ по отношению к новой плоскости проекций должен быть или фронталью (при замене плоскости V на плоскость V₁ ), или горизонталью (при замене плоскости Н на плоскость H₁).

Решим эту задачу двумя вариантами.

Первый вариант. Заменим плоскость V новой фронтальной плоскостью проекций V₁ (рис. 128, а).

Для упрощения построений новая ось проекций х₁ может совпадать с горизонтальной проекцией ab отрезка прямой. Координата z_B точки равна нулю (так как точка В расположена на плоскости H), поэтому новая фронтальная проекция b’₁ совпадает с прежней горизонтальной проекцией b.

Новая фронтальная проекция а’₁ точки А находится на перпендикуляре, восставленном к новой оси проекций x₁ . Отрезок а’₁ а, отложенный на этом перпендикуляре, равен расстоянию от прежней фронтальной проекции а’ точки А до прежней оси x или координате z_А точки А. Соединив точки a’₁ и b’₁ получим действительную длину отрезка АВ.

Второй вариант. Заменим плоскость H новой горизонтальной плоскостью проекций Н₁ (рис. 128, б).

Новую ось проекций х₁ проведем (для упрощения построений) через фронтальную проекцию отрезка а’₁b’₁. Координату у_А откладываем на перпендикуляре к новой оси x₁, от точки а’, а координату У_В — от точки b’. Отложив эти координаты, получаем новые горизонтальные проекции а₁ и b₁ точек A и B. Соединив точки а₁ и b₁, на новой горизонтальной плоскости проекций Н₁, получим действительную длину отрезка АВ.

Действительный вид плоской фигуры также можно определить способом перемены плоскостей проекций.

Для примера возьмем прямоугольный треугольник AВС (см. рис. 128, в), который расположен в горизонтально-проецирующей плоскости.

В данном примере заменяется плоскость проекций V новой плоскостью V₁ так, чтобы новая фронтальная проекция треугольника АВС была его искомым действительным видом. Новая ось проекций х₁ должна быть проведена на комплексном чертеже параллельно горизонтальной проекции треугольника или (для упрощения построений) так, как показано на рис 128, в, где новая ось х₁ совпадает с горизонтальной проекцией abc треугольника. В этом случае новые фронтальные проекции a’₁ и с’₁ совпадут с горизонтальными проекциями а и с вершин треугольника.

Для определения действительного вида треугольника остается найти только одну новую фронтальную проекцию третьей точки — вершины В. Для этого нужно из прежней горизонтальной проекции b точки В восставить перпендикуляр к новой оси проекций x₁ и от нее отложить на перпендикуляре расстояние от фронтальной проекции b’ до оси х или координату z_B . Соединив точку b’₁ с точками а’₁ и с’₁ прямыми линиями, получим действительный вид треугольника АВС.

Подобными приемами построений можно определить действительный вид многоугольника /2345, плоскость которого является фронтально-проецирующей (см. рис. 129).

В этом случае требуется заменить H на H₁, ось проекций которой проводится параллельно фронтальной проекции многоугольника на произвольном расстоянии.

Для нахождения, например, новой горизонтальной проекции точки 3 из точки 3′ восставляют перпендикуляр и от оси x₁, откладываем на этом перпендикуляре расстояние, равное расстоянию от точки 3 до оси x;. Точка З₁ будет новой горизонтальной проекцией точки 3. Так же находят точки 1₁,2₁,4₁ и 5₁ Затем, соединив их прямыми линиями, получают действительный вид многоугольника.

Построение действительного вида контура лопасти, расположенной в горизонтально-проецирующей плоскости, показано на рис. 130. В этом случае плоскость проекции V заменена новой плоскостью V₁ . Для упрощения построений новая ось проекций x₁ проведена через горизонтальную проекцию фигуры, а лопасть опущена вниз до соприкосновения с плоскостью Н.

Для определения действительного вида контура фигуры строят новые фронтальные проекции нескольких ее точек способом, описанным выше. Например, для построения новой фронтальной проекции какой-либо точки Е криволинейного контура лопасти из горизонтальной проекции е к новой оси проекций x₁ восставляют перпендикуляр, на котором от точки е откладывают отрезок, равный расстоянию фронтальной проекции е’ до оси х, т. е. координату z точки Е. е’₁ — новая фронтальная проекция точки Е.

Источник