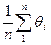Способ устранения систематическая погрешность

Способы обнаружения и устранения систематических погрешностей

Результаты наблюдений, полученные при наличии систематической погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей. Это может быть дос­тигнуто следующими путями:

• устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устра­нить систематические погрешности не путем обработки экспери­ментальных данных, а применением СИ, реализующих соответст­вующие методы измерений;

• определением поправок и внесением их в результат измерения;

Поправкой называется значение величины, одноименной с измеряемой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности. Введение поправок — наиболее широко используемый способ исключения систематических инструментальных погрешностей. Поправка определяется при помощи поверки технических средств, составления и использования соответствующих таблиц и графиков. Применяются также расчетные способы нахождения поправочных значений.

• оценкой границ неисключенных систематических погрешностей. Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Од­нако она не искажает ни показатели точности измерений, характе­ризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Дейст­вительно, результат одного измерения

где X_и — истинное значение измеряемой величины; Δ_i — i-я случай­ная погрешность; θ_i — i-я систематическая погрешность. После ус­реднения результатов многократных измерений получаем среднее арифметическое значение измеряемой величины

= x_и + +

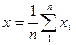
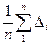
Если систематическая погрешность постоянна во всех измере­ниях, т.е. θ_i = θ, то

х =x_и + 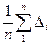+ θ.

Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях.

Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже.

Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и ап­проксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.

Для устранения постоянных систематических погрешностей при­меняют следующие методы:

• Метод замещения, представляющий собой разновидность ме­тода сравнения, когда сравнение осуществляется заменой измеряе­мой величины известной величиной, причем так, что при этом в состоянии и действии всех используемых средств измерений не про­исходит никаких изменений. Этот метод дает наиболее полное ре­шение задачи. Для его реализации необходимо иметь регулируе­мую меру, величина которой однородна измеряемой. Например, взвешивание по методу Борда, измерение сопротивления посред­ством моста постоянного тока и мер сопротивления.

• Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной по­грешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений. Например, способ взве­шивания Гаусса.

• Метод компенсации погрешности по знаку (метод изменения знака систематической погрешности), предусматривающий измерение с двумя наблюдениями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками.

• Метод рандомизации — наиболее универсальный способ ис­ключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется раз­личными методами (приборами). Систематические погрешности ка­ждого из них для всей совокупности являются разными случайны­ми величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности вза­имно компенсируются.

Для устранения переменных и монотонно изменяющихся сис­тематических погрешностей применяют следующие приемы и ме­тоды.

• Анализ знаков неисправленных случайных погрешностей. Ес­ли знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная система­тическая погрешность. Если последовательность знаков «+» у слу­чайных погрешностей сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся система­тическая погрешность. Если группы знаков «+» и «-» у случайных погрешностей чередуются, то присутствует периодическая система­тическая погрешность.

• Графический метод. Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей

• Метод симметричных наблюдений. Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y = kx + y₀, где х, у – входная и выходная величины преобразователя; k — коэффициент, погрешность которого изменяется во времени по линейному закону; у₀ — постоянная.

Для устранения систематической погрешности трижды измеря­ется выходная величина у через равные промежутки времени Δt. При первом и третьем измерениях на вход преобразователя подает­ся сигнал х₀ от образцовой меры. В результате измерений получа­ется система уравнений:

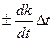
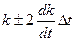
Y₁= kx₀ + у₀; Y₂ = ( k )x + у_0; Y₃ = ( )x₀ + y₀

Ее решение позволяет получить значение х, свободное от пере­менной систематической погрешности, обусловленной изменением коэффициента k:

.

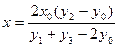
• Специальные статистические методы. К ним относятся спо­соб последовательных разностей, дисперсионный анализ, и др.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Систематические погрешности. Причины возникновения и способы исключения

Классификация погрешностей

Погрешности измерений

Результат любого измерения отличается от истинного значения измеряемой величины на некоторое значение, зависящее от принятой модели объекта, метода измерения, характеристик технических средств, квалификации оператора, условий при которых производится измерение. Отклонение результата измерения от истинного значения измеряемой величины называется погрешностью измерения. Погрешность является достаточно сложным понятием и нуждается в развитой системе классификации.

Абсолютная погрешность D выражается в единицах измеряемой физической величины:

где х — значение, полученное при измерении;

х_и — истинное значение измеряемой величины.

Указание абсолютной погрешности во многих случаях является удобным и естественным способом охарактеризовать точность измерений. Однако при этом не удается производить сравнение точности измерений в случаях, когда размеры измеряемых величин существенно отличаются друг от друга. Ясно, что, например, измерение расстояния 1 км с абсолютной погрешностью 1 см намного точнее, чем измерение с той же абсолютной погрешностью расстояния 1 м.

Относительная погрешность g_отн, равна отношению абсолютной погрешности измерения к истинному значению измеряемой величины:

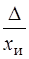
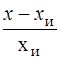
g_отн = = . (3.2)

Поскольку обычно абсолютная погрешность D много меньше истинного значения х_и, относительную погрешность g_отн удобно умножать на 100, выражая ее в процентах. Например, если в результате измерения напряжения было получено значение 225 В, тогда как истинное значение составляет 220 В, то абсолютная погрешность D = 225 — 220 = 5 В, относительная погрешность g_отн = 5 / 220 = 0,023 или g_отн = 2,3 %.

В зависимости от характера проявления погрешности делят на систематические, случайные и грубые (промахи). Такое разделение целесообразно для удобства обработки результатов измерений.

Систематической погрешностью измерения называется составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Причиной появления систематических погрешностей могут быть неисправности измерительной аппаратуры, несовершенство метода измерения, неправильная установка измерительных приборов и отступление от нормальных условий их работы, особенности и неправильные действия самого оператора. Систематические погрешности в принципе могут быть выявлены и почти полностью устранены. Для этого требуется проведение тщательного анализа возможных источников погрешностей в каждом конкретном случае. К сожалению, несмотря на все усилия, всегда остаются некоторые не исключенные, остаточные систематические погрешности. Задачей экспериментатора является определение их наибольших, граничных значений.

Случайной погрешностью измерения называется составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же физической величины. Наличие случайных погрешностей выявляется при проведении ряда измерений этой величины, когда оказывается, что результаты измерений не совпадают друг с другом. Если систематические погрешности исключены, то полученные при отдельных наблюдениях результаты вследствие случайных причин будут рассеяны в окрестности истинного значения. Если же систематические погрешности присутствуют, то результаты наблюдений будут соответственно смещены в сторону от истинного значения.

Обычно случайные погрешности возникают из-за одновременного действия многих случайных причин, каждая из которых в отдельности мало влияет на результат измерения. Поэтому нет простых способов избавиться от случайных погрешностей. Нужно либо коренным образом изменять условия измерительного эксперимента, либо удовлетвориться отысканием области, в которой лежит истинное значение измеряемой величины с заданной вероятностью. Математические дисциплины, устанавливающие поведение случайных величин, такие как теория вероятностей и математическая статистика, представляют для этого необходимые средства.

В некоторых случаях оказывается, что результат того или иного отдельного измерения резко отличается от результатов других измерений, выполненных при тех же контролируемых условиях. Причиной этого может быть ошибка оператора, возникновение сильной кратковременной помехи, толчок, нарушение электрического контакта и т.д. Естественно, что такой результат, содержащий грубую погрешность (промах), следует выявить, исключить и не учитывать при дальнейшей статистической обработке результатов. Надо сказать, что выявление грубых погрешностей не всегда является простой задачей. Для этого разработаны специальные процедуры, некоторые из которых будут описаны ниже в этой главе.

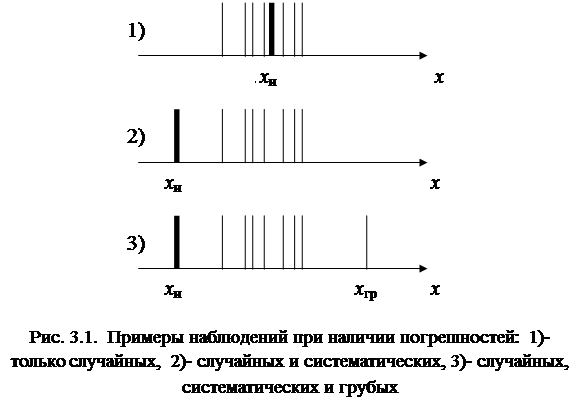
Рис.3.1 иллюстрирует рассеяние результатов наблюдений в окрестности истинного значения х_и для случаев, когда 1) — имеются только случайные погрешности, 2) — когда наряду со случайными погрешностями присутствует и систематическая составляющая, 3) — когда имеются все виды погрешностей, включая грубую (промах) при полученном результате одного из наблюдений х_гр.

Природа ипроисхождение систематических погрешностей обусловлены несовпадением принятых моделей объекта, средства измерения и измерительного процесса с реальными условиями. Такое несовпадение имеет место всегда. Но степень и последствия его различны. Они определяются спецификой конкретного эксперимента. Задачей измерений является обнаружение и по возможности более полная коррекция возникающих из-за этого систематических погрешностей. Ее решение во многом зависит от мастерства экспериментатора, от того, насколько глубоко он изучил конкретные условия и особенности применяемых им методов и средств. Вместе с тем существуют некоторые общие причины возникновения систематических погрешностей, а, следовательно, и общие приемы их обнаружения и исключения. В соответствии с причинами возникновения погрешности подразделяют на:

— методические,

— инструментальные,

— субъективные.

Методические погрешности происходят от несовершенства метода измерения, упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения.

В любом случае информацию о значении методической погрешности нельзя почерпнуть из нормативно-технической информации об используемом средстве измерения, например, из паспорта на него. Дело в том, чти методическая погрешность либо совсем не зависит от характеристик средства измерения, либо зависит относительно, то есть проявляется в каждом конкретном случае в различной степени.

Например, измерение высоты полета самолета барометрическим методом использует известную зависимость давления воздуха от высоты. Однако эта зависимость содержит такой параметр как температура воздуха. Можно учесть сведения о температуре за бортом и произвести необходимую коррекцию результата измерений. К сожалению, распределение температуры по высоте имеет очень сложный профиль, зависящий от многих причин и изменяющийся со временем. Поэтому приходится удовлетворяться знанием некоторой эффективной температуры, обеспечивающей лишь частичную коррекцию. В данном случае погрешность определяется выбранным методом измерения и не может быть исключена посредством каких бы то ни было манипуляций с барометром — прибором, который задействован для измерения высоты.

Нередко погрешности связаны с неточным знанием значений констант, входящих в расчетные формулы. Хрестоматийным примером является ошибка, которую допустил Р.Милликен при измерении элементарного электрического заряда e. Он в своем опыте наблюдал за движением заряженных капель масла в электрическом поле и при обработке результатов эксперимента использовал значение вязкости воздуха, которое оказалось заниженным. Что и привело к результату, содержащему неисключенную систематическую погрешность около 0,5 %. Затем эта погрешность перекочевала в значения многих физических величин и констант, при определении которых использовалось значение е, полученное Милликеном. Среди них оказались такие важные как постоянная Планка и число Авагадро. На то, чтобы найти и устранить все эти ошибки потребовалось почти три десятилетия.

Важным источником методических погрешностей является воздействие средства измерения на исследуемый объект. Например, измерение температуры массивным термометром может нарушить изучаемый тепловой режим и привести к получению искаженных результатов. Точно так же попытки произвести точные измерения напряжения в высокоомных электрических цепях вольтметром, имеющим недостаточно большое входное сопротивление, едва ли будут успешными. Внесение входного сопротивления вольтметра в такую цепь самым существенным образом нарушит ее работу и не позволит получить качественные результаты измерений. При измерениях в низкоомных цепях последствия не столь драматичны, но все равно шунтирование входным сопротивлением вольтметра участка цепи, на котором измеряется напряжение, приводит к погрешности. Эту погрешность следует считать методической, поскольку она определяется не столько свойствами прибора, сколько соотношением между его характеристиками и параметрами цепи.

Инструментальные погрешности измерения зависят от погрешностей применяемых средств измерения, то есть приборов, преобразователей, мер и т.п. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и некоторые другие причины вызывают появление инструментальных погрешностей. Невозможно создать идеальное средство измерения, совсем свободное от погрешностей. Однако есть возможность оценить предельные значения погрешностей реальных измерительных устройств. можно при конструировании приборов потребовать, чтобы их погрешности (абсолютные, относительные или приведенные) не превышали определенных, заранее установленных значений. В соответствии с такими максимально допускаемыми погрешностями средствам измерений приписывается тот или иной класс точности. Поскольку, как указывалось выше, требуемая точность определяется целью измерительного эксперимента, выбранное средство измерения должно иметь соответствующий класс точности, т.е. обеспечивать получение результатов измерений с приемлемой инструментальной погрешностью. К сожалению возможны случаи, когда в процессе измерения возникают инструментальные погрешности, превышающие те, что указаны в паспорте на применяемое средство измерения или соответствующие его классу точности в качестве максимально допускаемых. Это может случиться, например, из-за того, что поверка средств измерения производится периодически, а эксплуатация — непрерывно. Есть определенная вероятность, что в какой-то момент между поверками параметры прибора окажутся отличными от предполагаемых, а погрешности выйдут за допускаемые пределы.

Погрешности измерения возникают также из-за неправильной установки средства измерения, влияния на него магнитных и электрических полей, наличия дополнительных и динамических погрешностей. Дополнительные погрешности обусловлены отклонением условий, при которых работает прибор, от нормальных. Динамические погрешности возникают из-за инерционности применяемых технических средств при достаточно быстрых изменениях измеряемой величины. Все эти погрешности отличаются от инструментальных, поскольку они не столько связаны с самими средствами измерений, сколько с условиями, при которых они работают (ГОСТ 8.009-84). Их устранение производится иными способами, нежели устранение инструментальных погрешностей.

Субъективные погрешности вызываются неправильными отсчетами показаний прибора человеком (оператором). Это может случиться, например, из-за неправильного направления взгляда при наблюдении за показаниями стрелочного прибора (погрешность от параллакса). Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности. Компьютерные измерения также свободны от них.

Заметим, что выделение в составе систематических погрешностей методической, инструментальной, субъективной и других составляющих представляется естественным, так как отражает различные способы их исключения или оценки. Но это вовсе не означает то, что указанные погрешности (методические, инструментальные и прочие) всегда проявляют себя как систематические, то есть остаются постоянными или закономерно изменяются. При других обстоятельствах они могут вести себя случайно и относиться к случайным погрешностям.

Как уже отмечалось, обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению либо исключению посредством введения поправки.

Поправкой называется значение величины, одноименной с измеряемой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности. Таким образом, поправка численно равна абсолютной погрешности измерения, взятой с противоположным знаком.

В некоторых случаях используют поправочный множитель – число, на которое надо умножить результат измерения, чтобы исключить систематическую погрешность.

Поправка или поправочный множитель определяются при помощи поверки технического средства, составления и использования соответствующих таблиц и графиков, Применяются также расчетные способы нахождения поправочных значений.

Источник