Способ устного вычисления суммы

Различные способы устных вычислений

В данной работе описываются способы устного счета в школьном курсе — это приемы устных вычислений, основанные на законах и свойствах арифметических действий, и изучаются способы существующие в науке, не вошедшие в школьную программу.

Скачать:

Вложение	Размер
sveta_blagonravova.docx	67.91 КБ

Предварительный просмотр:

Да, путь познания не гладок.

Но знаем мы со школьных лет:

Загадок больше, чем разгадок,

и поискам предела нет!

В наше время бытует мнение, что вычислительная работа должна стать уделом компьютеров, а человек может отойти от этого рутинного занятия. Но существуют такие способы устных вычислений, которые выдают ответы моментально и не уступят никакому компьютеру.

Большой успех имеют на эстраде выступления счетчиков, которые удивляют зрителей своей высокой техникой счета и феноменальной памятью.

Все мы, конечно, понимаем, что это всего лишь фокус, основанный на свойствах чисел или на каких- либо математических законах. А на каких именно, хочется знать?

Немецкого ученого Карла Гаусса называли королем математиков. Его математическое дарование проявилось уже в детстве.

Рассказывают, что в трех летнем возрасте он удивил окружающих, поправив расчеты своего отца с каменщиками. Однажды в школе (Гауссу в то время было 10 лет) учитель подложил классу сложить все числа от 1 до 100. Пока он диктовал задание, у Гаусса уже был готов ответ. На его грифельной доске было написано: 101 х 50 = 5050. Интересно, как он быстро выполнил это задание?

У известного русского художника Богданова-Бельского есть картина «Устный счет», изображающая занятия устным счетом. Ученики заняты устным решением примера. Они сосредоточены и увлечены работой.

Здесь воспроизведена известная и любимая всеми учителями картина Богданова-Бельского «Устный счет». По поводу этой картины И. К. Андронов пишет так: «Одиннадцать бедных крестьянских учеников старой, досоветской школы с напряжением ищут в уме решение числовой формулы, написанной на доске учителем С. А. Рачинским. Как лучше сгруппировать слагаемые, как быстрее вычислить?

Немного из истории этой картины:

Устному счету уделял большое внимание известный русский деятель в области просвещения доктор естественных наук, профессор ботаники Московского университета Сергей Александрович Рачинский (1832-1902). В 1872 г. он переехал из Москвы в свое имение, село Татево Смоленской губернии. Там организовал начальную школу и сам преподавал в ней, стремясь развить у крестьянских детей математические способности и привить им интерес к математике. С.А. Рачинский написал ряд математических пособий. Наибольшую известность среди них приобрела книга «1001 задача для счета в уме».

Обратимся к картине. На доске записан пример для устного счета:

По-разному думают дети. Кто-то скорее мечтает, чем думает. Кто-то торопится шепнуть учителю свой ответ. Но внимание педагога поглощено одним мальчиком, вся поза которого напоминает охотника, идущего по следу,- столько в ней сдержанной страсти и предчувствия победы. Мальчик, конечно же, догадывается, что сумма квадратов первых трех натуральных чисел равна сумме квадратов следующих чисел, т.е. Таким образом, данное на картине числовое выражение равно 2.

Вспомним, как относились к устному счету ученики С. А. Рачинского. Он писал: «Не успел я приступить к упражнениям в умственном счете, которые до тех пор в школе не практиковались, как к ним развилась настоящая страсть… Стали меня преследовать то одна группа учеников, то другая, то все вместе с требованием умственных задач… Очень скоро оказалось, что они опережают меня, что мне нужно готовиться, самому упражняться».

На уроках математики учитель часто говорит: «Для выполнения этого громоздкого задания, примените рациональные методы, и тогда пример решается устно».

Все эти моменты и заставили меня изучить хотя бы некоторые методы для выполнения устных вычислений.

В своей работе я хочу показать некоторые способы устного счета.

1. Обобщить способы устного счета в школьном курсе и изучить существующие в науке (расширить знания по этому вопросу).

а) Некоторые приемы устных вычислений, основанные на законах и свойствах арифметических действий, а именно:

Использование свойства вычитания суммы из числа и числа из суммы.

Использование переместительного и сочетательного свойства сложения и умножения.

Использование распределительного свойства умножения относительно сложению и вычитанию

Использование таблицы квадратов и кубов однозначных чисел и таблицы квадратов двузначных чисел от 10 до 20.

б) Умножение двузначных чисел на 11.

в) Использование формул сокращенного умножения:

(a ± b)² = a² ± 2ab + b²

г) Возведение в квадрат чисел оканчивающихся на 5.

д) Умножение чисел на 5 (50), 25 (250).

е) Умножение двузначных чисел близких к 100.

2. Показать практическую значимость каждого метода.

3. Обобщить данное исследование.

1. Повышение вычислительной культуры учащихся (Пособие для учителя)М. Просвещение 1981г.
2. А. П. Подашов «Вопросы внеклассной работы по математике в школе». Учпедгиз 1962г.
3. Д. С. Фаермарк «Задача пришла с картины». М. Просвещение, 1977г.
4. О. С. Шенина , Г. М. Соловьева «Математика. Занятия школьного кружка.» М.Издательство НЦ ЭНАС 2007.
5. Журнал «Математика в школе» №2 1981г, Журнал «Математика в школе» №1 1992г.

Познакомившись с материалами по данной теме в указанной литературе, я решила показать в своей работе некоторые методы устных вычислений.

Некоторые приемы устных вычислений, основанные на законах и свойствах.

а. Использование свойств вычитания суммы из числа и числа из суммы.

а — (в + с) = (а + в) — с.

95837 — (95137 + 198) = (95837 — 95137) – 198 = 700 – 198 = 502.

(а + в) – с = (а — с) + в.

(6112 + 1596) – 496 = 6112 + (1596 — 496) = 6112 + 1100 = 7212.

б. Использование переместительного и сочетательного свойств сложения и умножения.

а + в + с = (а + в) + с = (а + с) + в = а + (с + в).

385 + 548 + 615 = (385 + 615) + 548 = 1000 + 548 = 1548.

2,31 + 7,65 + 8,69 = (2,31 + 8,69) + 7,65 = 11+7,65 = 18,65.

а х в х с = (ахв)с = а(вхс) = (ахс)в.

483 х2 х 5 = 483 х 10 = 4830.

25 х 86 х 4 = (25 х 4)86 = 860.

1,25 х 75 х 8 = (1,25 х 8)75 = 10 х 75 = 750.

в. Использование распределительного закона умножения относительно сложения и вычитания.

1. Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.

10(12 + 3) = 10 х 12 + 10 х 3 = 120 + 30 = 150,

(4,5 + 0,75)100 = 450 + 75 = 525,

3 х 3=(3 + )3 = 9 + 2 = 11.

Вычислите сумму, используя распределительный закон:

289 х 315 + 711 х 315 = 315(289 + 711) = 315 х 1000 = 315000,

14,8 х 36 + 14,8 х 64 = 14,8(36 + 64) = 14,8 х 100 = 1480,

3 + = (3 6 )= х 10 = 6,

— х(- 6,81) + (- 1,19)х(- ) = — х(- 6,81 – 1,19) = — (- 8) = 3,

2. Для того, чтобы умножить разность на число, можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.

59 х 7 = (60 – 1)7 = 420 – 7 = 413,

126 х 5 – 96 х 5 = (126 – 96)5 = 30 х 5 = 150,

0,78 х 496,6 – 396,6 х 0,78 = (496,6 – 396,6)0,78 = 100 х 0,78 = 78,

14 х = (14 — 3 ) = 3.

Для того чтобы быстро и безошибочно находить значения выражений, необходимо запомнить таблицу квадратов и кубов и, желательно, таблицу квадратов чисел от 11 до 20.

Источник

«Методика изучения устного сложения и вычитания чисел».

Методика изучения устного сложения и вычитания чисел.

Устные приемы сложения и вычитания. Используют следующие устные приемы сложения и вычитания:

• сложение и вычитание на основе знания нумерации чисел — сложение и вычитание целых сотен и единиц, целых сотен и десятков: (500 + 7, 507 — 7, 507 — 500; 500 + 30, 530 — 30, 530 — 500; 500 + 67, 567 — 67, 567 — 500), прибавление и вычитание единицы (693 + 1, 799 + 1, 472 — 1, 600 — 1);

• сложение и вычитание разрядных сотен (300 + 100, 300 + 200, 400 — 100, 400 — 200);

• сложение целых десятков и соответствующие случаи вычитания (80 + 50, 130 — 50; 340 + 70, 410 — 70; 640 + 320, 960 — 320; 340 + 60, 400 — 60);

• сложение трехзначных чисел и разрядных единиц, десятков, сотен без перехода через разряд и соответствующие случаи вычитания (640 + 300, 940 — 300; 640 + 30, 670 — 30; 456 + 2, 458 — 2).

Изучая нумерацию чисел в пределах тысячи, учащиеся осваивают счет сотнями, потом сотнями и десятками, и далее сотнями, десятками и единицами, записывают и решают соответствующие примеры (300 + 100, 300 — 100, 300 + 10, 350 + 10, 300 — 10, 350 — 10, 599 + 1, 345 + 1, 500 — 1, 345 — 1), учатся заменять трехзначное число суммой разрядных слагаемых и применять данное умение при выполнении арифметических действий, например: 599 + 1 = (500 + 99) + 1=500 + (99 + 1) = 500 + 100 = 600.

С опорой на знание поразрядного строения числа выполняется сложение и вычитание целых сотен и единиц, целых сотен и десятков. Рассуждения:

500 + 67 (К 500 прибавляем 67. В числе 500 в разряде десятков и единиц стоит нуль, прибавляем 6 десятков и 7 единиц числа 67. Значение суммы состоит из 5 сотен, 6 десятков и 7 единиц, это число 567); 567 — 67 (Из 567 вычитаем 67. Число 567 состоит из 5 сотен, 6 десятков и 7 единиц. Вычитаем 6 десятков и 7 единиц числа 67. Остается 5 сотен. Значение разности — 500).

Прием прибавления и вычитания единицы основан на знании свойства натурального ряда чисел. Учащиеся осваивают применение своих знаний и умений в получении предыдущего и последующего чисел при выполнении операций с трехзначными числами.

После обучения считать сотнями (увеличивать и уменьшать разрядные сотни на сто), демонстрации взаимосвязи образования однозначного, двузначного и трехзначного чисел предлагается рассмотреть прием сложения и вычитания разрядных сотен, например, 300 + 200, который сводится к сложению и вычитанию однозначных чисел: 3 с.+2 с.=5 с.

Сложение целых десятков и соответствующие случаи вычитания можно соотнести со сложением и вычитанием однозначных и двузначных чисел, например, 80 + 50 = 8 д. + 5 д., 130 – 50 = 13 д. — 5 д., 640 + 320 = 64 д. + 32 д., 340 + 60 = 34 д.+ 6д., 640 – 320 = 64 д. — 32 д. Для этого необходимо повторить приемы сложения и вычитания в пределах ста, упражняться в определении количества десятков в числе. Можно использовать правило прибавления суммы к числу и суммы к сумме, правило вычитания суммы из числа. Если учащиеся еще не познакомились с этими правилами в соответствии с программой, то можно использовать уже известное им правило сложения и вычитания разрядных единиц: «Складывай единицы с единицами, десятки с десятками, вычитай единицы из единиц, десятки из десятков», которое дополняется требованием складывать сотни с сотнями (вычитать сотни из сотен).

Можно познакомить учащихся с разными приемами вычисления и предложить другой способ.

640 + 320 (К 640 прибавляем 320. Второе слагаемое (320) состоит из 3 сотен и 2 десятков, прибавляем к 640 сначала 300, потом еще 20, получаем 960), 640 + 320 = 640 + (300 + 20) = (640 + 300) + 20 = 940 + 20 = 960.

130 — 50 (Из 130 вычитаем 50. В уменьшаемом разрядных десятков меньше, чем в вычитаемом, поэтому вычитаемое вычитаем по частям и представляем его в виде удобных слагаемых (30 и 20). Вычитаем из 130 сначала 30, потом еще 20, получаем 80), 130 – 50 = 130 — (30 + 20) = 130 – 30 – 20 = 80.

640 — 320 (Из 640 вычитаем 320. Вычитаемое 320 состоит из 3 сотен и 2 десятков, вычитаем из 640 сначала 300, потом 20, получаем 320), 640 – 320 = 640 — (300 + 20) = 640 – 300 – 20 = 320.

Знание нумерации чисел, умение выполнять поразрядное сложение и вычитание применяются для выполнения сложения и вычитания трехзначных чисел. Например, складывая 640 и 300, учащиеся могут рассуждать следующим образом: «К 640 прибавляем 300. В числе 640 содержится 6 сотен и 4 десятка. Увеличиваем 6 сотен на 3 сотни, получаем 9 сотен, и еще прибавляем 4 десятка. Получаем 940». При выполнении вычитания 940-300 рассуждения следующие: «Из 940 вычитаем 300. В числе 940 содержится 9 сотен и 4 десятка, из 9 сотен вычитаем 3 сотни, остается 6 сотен и еще 4 десятка. Получаем 640».

Сложение трехзначных чисел и разрядных единиц, десятков, сотен без перехода через разряд и соответствующие случаи вычитания основаны на правиле группировки слагаемых, вычитания числа из суммы и сводятся к поразрядному сложению и вычитанию, например:

643 + 300 = (600 + 40 + 3) + 300 = (600 + 300) + 40 + 3 = 943. Рассуждения: К 643 прибавляем 300. Заменяем 643 суммой разрядных слагаемых. В этом числе 6 сотен, 4 десятка и 3 единицы. К 6 сотням прибавляем 3 сотни, получаем 9 сотен, к ним прибавляем 4 десятка и 3 единицы. Получаем 943.

675 — 30 = (600 + 70 + 5) – 30 = 600 + (70 — 30) + 5 = 600 + 40 + 5 = 645. Рассуждения: Из 675 вычитаем 30. Раскладываем 675 на сумму разрядных слагаемых. В этом числе 6 сотен, 7 десятков, 5 единиц. Из 7 десятков вычитаем 3 десятка, получаем 4 десятка. Складываем 6 сотен, 4 десятка и 5 единиц. Получаем 645.

После ознакомления с устными приемами вычисления целесообразно предлагать учащимся выполнять данные примеры на каждом уроке на этапе устного счета.

Раскрывая любой из приемов сложения и вычитания, рекомендуется решать примеры с подробной записью только при первичном знакомстве, затем довольно скоро следует переходить к кратким пояснениям и краткой записи решения и, наконец, к быстрым устным вычислениям без записи решения.

Для выработки навыков вычислений используют разнообразные письменные и устные упражнения: решение примеров в одно и более действий, нахождение числовых значений выражений при данных значениях букв, решение уравнений, сравнение выражений и запись числовых равенств и неравенств и др.

Применение знакомых детям свойств к новой области чисел позволяет значительно усилить самостоятельность работы учащихся при изучении нового материала. Это помогает также сформировать в короткое время осознанные вычислительные навыки и приступить к расширению знаний о свойствах действий. Учащиеся самостоятельно могут установить, как можно

прибавлять число к сумме трех слагаемых и вычитать число из суммы трех слагаемых; как прибавлять сумму трех слагаемых к числу и вычитать сумму трех слагаемых из числа; как сложить сумму с суммой и вычесть сумму из суммы нескольких слагаемых. Работа над этими правилами подготавливает детей к изучению следующей темы.

Источник

Как быстро считать в уме: приемы устного счета больших чисел

• 12 января 2021 г.
• 15 минут
• 279 263
• 9

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

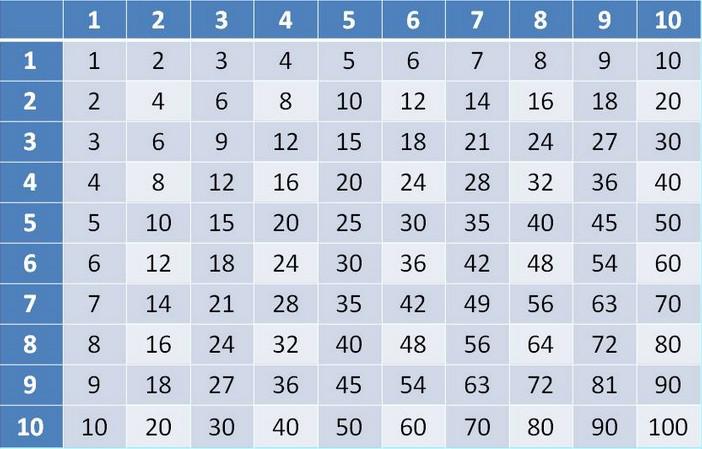
Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник