Приемы установления взаимно-однозначного соответствия
Деятельности учащихся в дочисловой (подготовительный) период
Дети к началу обучения имеют разный уровень подготовки. Поэтому задачей подготовительного этапа является выявление и уточнение следующих знаний и умений:
1) сравнивать численности двух множеств;
2) пересчитывать предметы множества, содержащего не более 10 предметов с помощью количественных и порядковых числительных; по результатам пересчета отвечать на вопрос «Сколько…?»;
3) иметь представление о порядковых и пространственных отношениях (больше, меньше, столько же, перед, после, между, следовать за, предшествовать, ниже, выше, левее, правее);
4) выполнять на элементарном уровне умственные операции: анализ, синтез, сравнение, классификацию.
5) готовность руки к письму (пишут палочки, обводят клетки, узоры, раскрашивают).
Продолжительность подготовительного периода зависит от уровня подготовки класса (от 1 до 3-х недель).
Опишем методику работы над этими вопросами программы.
Сравнение численности множеств. Не прибегая к операции счета, ребенок может ответить на такие вопросы как: «Больше?», «Меньше?», «Столько же?», устанавливая взаимно-однозначное соответствие между элементами различных множеств.
· наложение предметов одного множества на предметы другого;
· расположение предметов одного множества под предметами другого;
· попарное соединение предметов на рисунке линией (стрелкой);
· попарное перечеркивание предметов;
· изымание по одному предмету из каждого множества и откладывание получаемых пар.
Пересчитывание предметов множества. Установление взаимно-однозначного соответствия между предметными множествами связано с вычленением отдельных элементов и подготавливает детей к сознательному овладению операцией счета. При этом необходимо различать понятия «сознательный счет» и «механический счет». Для овладения операцией счета необходимо запомнить порядок слов-числительных (механический счет). Упражнять в этом ребенка следует, начиная с 3-4 лет. Большинство детей, поступающих в школу, уже владеют этим навыком, хотя ошибки возможны (пропуск числительных или предметов при счете).
Сознательное усвоение детьми действий счета предполагает следующее:
1) знание названий и последовательности десяти чисел натурального ряда;
2) понимание того, что для ответа на вопрос «Сколько?» надо пересчитывать предметы;
3) умение соотносить число и предмет при счете, не пропуская предметы и не называя их дважды;
4) понимание того, что последнее из названных при счете числительных дает ответ на вопрос: «Сколько?»
5) понимание того, что результат счета не зависит от порядка счета и расположения предметов.
Представление о порядковых и пространственных отношениях. В подготовительный период необходимо организовывать также и порядковый счет, знакомя с отношениями «следовать за» и «предшествовать». Важно упражнять детей в выполнении счета в прямой и в обратной последовательности.
Для формирования умственных операций предлагаются различные задания: «Что изменилось?», «Чем похожи рисунки, чем отличаются?», «Найди лишнюю картинку» и т.д. Работа проводится относительно разных признаков (цвет, размер, количество, форма и др.). Эти задания также сопровождаются счетом анализируемых предметов. Вся работа проводится устно: практические действия со счетным материалом сочетаются с рисованием, раскрашиванием. Также формируются пространственные умения. Например: «найдите картинку в верхнем левом углу страницы»; «отступите от края тетради слева и сверху по 1 клетке и поставьте точку в центре клетки».
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Лекция17. Взаимно-однозначные соответствия
1. Взаимно-однозначные соответствия. Понятие взаимно однозначного отображения множества Х на множество Y.
2. Равномощные множества. Способы установления равномощности множеств. Счетные и несчетные множества.
3. Основные выводы
Взаимно однозначные соответствия. Понятие взаимно однозначного отображения множества Х на множество Y
В математике изучают различные виды соответствий. Это не случайно, поскольку взаимосвязи, существующие в окружающем нас мире, многообразны. Для учителя, обучающего математике младших школьников, особую значимость имеют взаимно однозначные соответствия.
Определение. Взаимно однозначным соответствием между множествами X и Y называется такое соответствие, при котором каждому элементу множества X сопоставляется единственный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества X.
Рассмотрим примеры взаимно однозначных соответствий.
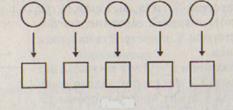
Пример 1. Пусть Х — множество кружков, Y — множество квадратов и соответствие между ними задано при помощи стрелок (рис. 76).
Рис. 76
Это соответствие взаимно однозначное, так как каждому кружку из множества X сопоставляется единственный квадрат из множества Y и каждый квадрат из Y соответствует только одному кружку из множества X.
Пример 2. Пусть X — множество действительных чисел, Y — множество точек координатной прямой.Соответствие между ними таково: действительному числу сопоставляется точка координатной прямой. Это соответствие взаимно однозначное, так как каждому действительному числу сопоставляется единственная точка координатной прямой и каждая точка на прямой соответствует только одному числу.
В математике взаимно однозначное соответствие между множествами X и Y часто называют взаимно однозначным отображение множества X на множество Y.
Понятие взаимно однозначного соответствия позволяет определитьотношение равномощности множеств.
Дата добавления: 2016-05-11 ; просмотров: 1986 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Большая Энциклопедия Нефти и Газа
Установление — взаимно однозначное соответствие
Установление взаимно однозначного соответствия дает возможность сравнивать множества с бесконечным числом элементов. [1]
Существует несколько способов установления взаимно однозначных соответствий между оригиналом и его проекциями. Эти свойства изложены ниже. [2]
В некоторых случаях для установления взаимно однозначного соответствия между числовыми множествами бывает полезно числа, входящие в эти множества, записывать с помощью систематических дробей. [3]
Основной целью этого параграфа является установление взаимно однозначного соответствия между компактными группами Ли и редуктивными комплексными алгебраическими группами, а также между гомоморфизмами компактных и редуктивных групп. На языке теории категорий это означает, что имеется эквивалентность между категориями компактных групп Ли и редуктивных комплексных алгебраических групп. Важным следствием является теорема о полной приводимости линейных представлений полупростых алгебр Ли. Существенную роль в развитой здесь теории играет теорема о полярном разложении, которую мы доказываем в вещественной ситуации, имея в виду дальнейшие применения. Одним из них является доказательство связности множества вещественных точек односвязной комплексной полупростой алгебраической группы, определенной над К. [4]
Теперь легко вывести ( аналитически или посредством установления взаимно однозначного соответствия ) следующую формулу, высказанную Дхаром в [12] как предположение. [5]
Процедура, которая производится в указанном примере, описываемая абстрактным образом, есть установление взаимно однозначного соответствия между множествами А и В. [6]
Таким образом, матрица Re может содержать не более k различных клеток порядка / с точностью до установления взаимно однозначного соответствия . [7]
Заметим теперь, что если первый способ ( подсчет числа элементов) годится лишь для сравнения конечных множеств, второй ( установление взаимно однозначного соответствия ) пригоден и для бесконечных. [8]
Ради простоты рассмотрим вопрос о введении координат на прямой. Возможность введения координат на прямой основывается на возможности установления взаимно однозначного соответствия между множеством всех точек прямой и множеством всех вещественных чисел. Доказательство возможности установления такого соответствия базируется на аксиомах геометрии и на аксиомах ( свойствах) множества вещественных чисел) и приводится в Приложении к настоящей книге. [9]
Избранный им способ сравнения двух множеств заключается в установлении взаимно однозначного соответствия между их элементами. Этот способ представляет собой как бы объединение элементов одного множества в пары с элементами другого множества, причем так, что каждый элемент входит в одну-единственную пару. [10]
Ясно, что множества можно сравнивать не только с множеством натуральных чисел; установление взаимно однозначного соответствия ( биекции) позволяет сравнивать между собой любые два множества. [11]
Структурная схема ПУВГИ изображена на рис. 2.4. Основная задача ПУВГИ — определение координат в некотором поле, в котором располагается чертеж. Для решения этой задачи поле значений координат моделируется некоторой дискретной или непрерывной функцией с помощью блока моделирования. Блок соответствия необходим для установления взаимно однозначного соответствия между значениями координат точек чертежа, указанных оператором, и значениями функций, моделирующих поле координат. Блок измерения определяет значения моделирующих функций и преобразует их для передачи в ЭВМ. [13]
Аксиоматический метод закладывает фундамент и для лежащего в основе аналитической геометрии метода координат. Ради простоты рассмотрим вопрос о введении координат на прямой. Возможность введения координат на прямой основывается на возможности установления взаимно однозначного соответствия между множеством всех точек прямой и множеством всех вещественных чисел. Доказательство возможности установления такого соответствия базируется на аксиомах геометрии и на аксиомах ( свойствах) множества вещественных чисел 3) и приводится в Приложении к настоящей книге. [14]
Во-первых, была разработана система ACVC для верификации трансляторов с языка Ада [61], обеспечивающая их проверку на соответствие стандарту на язык Ада [4] с целью получения сертификата Министерства обороны США. Министерство обороны США объявило также о том, что для создания программного обеспечения по его заказу могут быть использованы только те трансляторы с языка Ада, которые успешно прошли проверку через систему ACVC и получили сертификат Министерства обороны США, оказывая тем самым прямое финансовое давление для достижения поставленной им цели. Столь сильное стремление к установлению взаимно однозначного соответствия между описанием языка программирования и реализациями трансляторов с этого языка программирования должно привести в случае своего выполнения к существенным преимуществам такого языка программирования перед другими. [15]
Источник
Педагогика в системе (стр. 10 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 |
33.1 Восприятие — форма целостного отражения предметов и явлений при их непосредственном воздействии на органы чувств. Именно восприятие больше всего связано с преобразованием информации, поступающей из внешней среды. В результате этого формируются психические образы, которыми в дальнейшем оперируют внимание, память, представление, воображение, мышление, эмоции. Важнейшие свойства восприятия — предметность, целостность, константность и обобщенность. Предметность — это отнесенность восприятия к отображаемому объекту, способность выделять предмет из окружающего фона как отдельно взятую вещь. Целостность — органическая взаимосвязь частей и целого в образе. Константность — относительная независимость образа от физических условий восприятия, проявляющаяся в его неизменности. Обобщенность — отнесенность каждого образа к некоторому классу объектов, имеющих название. Все эти свойства не являются врожденными и развиваются в течение всей жизни человека.
У младших школьников восприятие уже хорошо развито. Они не только различают цвет, форму, величину предметов и их положение в пространстве, но и могут правильно назвать предлагаемые формы и цвета, правильно соотнести предметы по их величине. Они могут изобразить простейшие формы и раскрасить их в заданный цвет. особенностью восприятия младших школьников является его тесная связь с действиями. Для младшего школьника воспринять предмет — значит что-то сделать с ним. Очень важно, чтобы дети в этом возрасте умели устанавливать идентичность предметов тому или иному эталону. Эталоны — это выработанные человечеством образцы основных разновидностей качеств и свойств предметов. Если ребенок может правильно назвать цвет и форму предмета, если он может соотнести воспринимаемое качество с эталоном, то он может установить идентичность.
В зависимости от того, какой анализатор играет в восприятии преобладающую роль, различают зрительное, слуховое, осязательное, кинестезическое, обонятельное и вкусовое восприятие. При восприятии времени большýю роль играют, помимо слуховых и зрительных ощущений, двигательные и внутренние, органические ощущения.
Избирательность восприятия . Младшие школьники лучше замечают ярко окрашенные предметы, подвижные предметы на фоне неподвижных. Они полнее и лучше воспринимают рисунок, который учитель выполняет при них на доске, чем тот же рисунок, показываемый уже в готовом виде. Все, что включено в трудовую, учебную, игровую деятельность самого ребенка и тем самым вызывает его активность и повышенный интерес, воспринимается более полно. Разнообразные практические занятия и упражнения ведут к более глубокому восприятию и, следовательно, к познанию предметов и явлений. Апперцепция — это зависимость восприятия от общего содержания психической жизни человека, его опыта и знаний, интересов, чувств и определенного отношения к предмету восприятия.
Иногда наши органы чувств подводят нас, как бы обманывают. Такие «обманы» органов чувств называют иллюзиями. Обычно школьники с большим интересом относятся к проблеме иллюзии восприятия. Наблюдение и наблюдательность. Наблюдением называют целенаправленное, планомерное восприятие. Наблюдать — это не просто смотреть, а рассматривать, не просто слушать, а вслушиваться, прислушиваться, не просто нюхать, а принюхиваться. Наблюдение характеризуется большой активностью личности. Наблюдательность у детей развивается постепенно. Воспринять учебный материал — это всегда значит как-то его осмыслить и так или иначе к нему отнестись.
Учитель стоит перед классом и объясняет. Мальчики и девочки внимательно слушают и воспринимают то, что он рассказывает. Но за этой одинаковой формой поведения, за этими внимательными глазами кроется сугубо индивидуальная мыслительная деятельность.
34.1 Память как психологическое понятие. Память – это запоминание, сохранение и последующее воспроизведение индивидом его опыта. С ее помощью отражение внешних воздействий постоянно используется индивидом в его дальнейшем поведении, за счет накопления индивидуального опыта происходит постепенное усложнение поведения. В памяти различают следующие основные процессы: запоминание, сохранение, воспроизведение и забывание.
Виды памяти дифференцируются в зависимости от того, что запоминается или воспроизводится.
1. По характеру психической активности, преобладающей в деятельности, память делят на:двигательную;эмоциональную;образную;словесно-логическую.
Двигательная память — это запоминание, сохранение и воспроизведение различных движений и их систем. Обычно признаком хорошей двигательной памяти является физическая ловкость человека.
Эмоциональная память – это память на чувства. Эмоции всегда сигнализируют о том, как удовлетворяются потребности и интересы индивида, как осуществляются отношения с окружающим миром. Образная память – это память на представления, картины природы и жизни, на звуки, запахи, вкусы. Делится на зрительную, слуховую, осязательную, обонятельную, вкусовую.
Содержанием словесно-логической памяти являются наши мысли. Этому виду памяти принадлежит ведущая роль в усвоении знаний учащимися в процессе обучения.
2. По характеру целей деятельности память делится на:непроизвольную;произвольную.
Запоминание и воспроизведение, в котором отсутствует специальная цель что-то запомнить или припомнить, называется непроизвольной памятью. В тех случаях, когда мы ставим такую цель, говорят о произвольной памяти. Непроизвольная и произвольная память представляют собой две последовательные ступени развития памяти.
3. По продолжительности закрепления и сохранения материала память делится на:кратковременную;долговременную;оперативную.
В отличие от долговременной памяти, для которой характерно длительное сохранение материала после многократного его повторения и воспроизведения, кратковременная память характеризуется очень кратким сохранением после однократного, очень непродолжительного восприятия и немедленным воспроизведением.
Понятием «оперативная память» обозначают мнемические процессы, обслуживающие непосредственно осуществляемые человеком актуальные действия, операции.
В младшем школьном возрасте память, как и все другие психические процессы, претерпевает существенные изменения. Как уже указывалось, суть их состоит в том, что память ребенка постепенно приобретает черты произвольности, становясь сознательно регулируемой и опосредствованной. У первоклассников хорошо развита непроизвольная память, фиксирующая яркие, эмоционально насыщенные для ребенка сведения и события его жизни.
Совершенствование памяти в младшем школьном возрасте обусловлено в первую очередь приобретением в ходе учебной деятельности различных способов и стратегий запоминания, связанных с организацией и обработкой запоминаемого материала. Однако без специальной работы, направленной на формирование таких способов, они складываются стихийно и нередко оказываются непродуктивными.
Способность детей младшего школьного возраста к произвольному запоминанию неодинакова на протяжении обучения в начальной школе и существенно различается у учащихся I–II и III–IV классов. Процесс развития логической памяти у младших школьников должен быть специально организован, поскольку в подавляющем большинстве дети этого возраста самостоятельно не используют приемы смысловой обработки материала и с целью запоминания прибегают к испытанному средству – повторению. Младший школьный возраст сенситивен для становления высших форм произвольного запоминания, поэтому целенаправленная развивающая работа по овладению мнемической деятельностью является в этот период наиболее эффективной. Важным ее условием является учет индивидуальных характеристик памяти ребенка; ее объема, модальности (зрительная, слуховая, моторная) и т. п. Но независимо от этого каждый ученик должен усвоить основное правило эффективного запоминания: чтобы запомнить материал правильно и надежно, необходимо с ним активно поработать и организовать его каким-либо образом.
34.2 Различные смыслы натурального числа и их раскрытие в учебниках математики для начальной школы.
Суть отношения «непосредственно следовать за» раскрывается в следующих аксиомах Пеано.
Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей и обозначают символом 1.
Аксиома 2. Для каждого элемента и из N существует единственный элемент а’, непосредственно следующий за а.
Аксиома 3. Для каждого элемента о из N существует не более одного элемента, за которым непосредственно следует а.
Аксиома 4. Всякое подмножество М множества 14, обладающее свойствами: 1) 1 ϵ М; 2) из того, что а содержится в М, следует, что и а’ содержится в М, совпадает с множеством N.
Определение. Множество N для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам 1 — 4, называют множеством натуральных чисел, а его элементы — натуральными числами.
Определение. Если натуральное число b непосредственно следует за натуральным числом а, то число а называется непосредственно предшествующим (или предшествующим) числу b .
Отношение «предшествует» обладает рядом свойств. Они формулируются в виде теорем и доказываются с помощью аксиом 1—4.
Теорема 14.1. Единица не имеет предшествующего натурального числа.
Теорема 14.2. Каждое натуральное число а, отличное от 1, имеет предшествующее число b , такое, что b ‘ = а.
Теоретико-множественный смысл натурального числа.
Натуральное число — это общее свойство класса конечных равномощных множеств.
Число «нуль» с теоретико-множественных позиций рассматривается как число элементов пустого множества.
Итак, натуральное число а как характеристику количества можно рассматривать с двух позиций:
1) как число элементов в множестве А, получаемое при счете, т. е. а = п(А), причем А
2) как общее свойство класса конечных равномощных множеств.
Смысл натурального числа, полученного в результате измерения величины.
Определение. Считают, что отрезок х состоит из отрезков х1, х2, . х n , если он является их объединением и никакие два из них не имеют общих внутренних точек, хотя и могут иметь общие концы.
Определение. Если отрезок х состоит из отрезков, каждый из которых равен единичному отрезку е, то число а называют численным значением длины данного отрезка при единице длины Е.
Из данного определения получаем, что натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется. При выбранной единице длины Е это число единственное.
В связи с таким подходом к натуральному числу сделаем два замечания:
1. При переходе к другой единице длины численное значение длины заданного отрезка изменяется, хотя сам отрезок остается неизменным.
2. Если отрезок х состоит из а отрезков, равных е, а отрезок у — из b отрезков, равных е, то а = b тогда и только тогда, когда отрезки х и у равны.
Огромная роль числа в жизни людей обусловливает довольно раннее формирование числовых представлений у ребенка. Уже в 2-3 года, отвечая на вопрос, сколько ему лет, малыш показывает два или три пальчика и называет соответствующее слово-числительное, обозначающее количество пальцев (предметов). В общении со взрослыми и в игре у него расширяется запас числовых представлений. В его речи появляются новые слова-числительные, которые он соотносит с определенными образами (два глаза, два уха, один нос, пять пальцев и т. д.).
Натуральное число выступает для ребенка на этом этапе как целостный наглядный образ, в котором он не выделяет единичных предметов. Наглядный образ числа находит свое выражение и в «числовых фигурах», каждую из которых ребенок соотносит с определенным словом-числительным. Уже в 4 года он может легко усвоить правила игры в «Домино», ориентируясь на «числовые фигуры», и непроизвольно запомнить их названия, закодировав тем самым каждый образ определенным словом, обозначающим число.
Количественная характеристика предметных групп осознается ребенком и в процессе установления взаимно-однозначного соответствия между предметными множествами. В этом случае количественная характеристика числа находит выражение в понятиях «столько же», «больше», «меньше».
Для установления взаимно-однозначного соответствия между предметными совокупностями можно использовать: 1) Наложение предметов одного множества на предметы другого; 2) Расположение предметов одного множества под предметами другого; 3) Образование пар, т. е. соединение каждого предмета одного множества с каждым предметом другого.
Установление взаимно-однозначного соответствия между предметными множествами связано с вычленением отдельных элементов и подготавливает детей к сознательному овладению операцией счета.
На первом этапе счет выступает для ребенка как установление взаимно-однозначного соответствия между предметной совокупностью и совокупностью слов-числительных, расположенных в определенном порядке.
Деятельность, связанная с усвоением порядка слов-числительных, естественно, выполняется по образцу и закрепляется в процессе однотипных упражнений, начинающихся со слова: «Сколько. » Начинать выполнять эти упражнения полезно как можно раньше (с 3 — 4 лет), постепенно увеличивая количество пересчитываемых предметов. В этом случае ребенок сможет непроизвольно запомнить последовательность слов-числительных.
Большинство детей шестилетнего и семилетнего возраста, поступающих в школу, уже владеют этим навыком, хотя ошибки возможны.
Усвоение детьми последовательности слов-числительных позволяет учителю перейти к формированию операции счета и к знакомству учащихся с символическим обозначением каждого числа (цифрами). При этом не обязательно ориентироваться на порядок чисел в натуральном ряду. Можно, например, сначала научиться писать цифру 4, затем 1, затем 6, 9 и т. д. Рекомендуем также познакомить учеников с другими обозначениями некоторых чисел..Например, с римскими цифрами.
Это поможет младшим школьникам дифференцировать такие понятия, как «число» и «цифра». Так как каждому предмету группы ребенок ставит в соответствие определенное слово-числительное, то в процессе счета он легко осознает порядковую характеристику числа, которая находит свое выражение в словах: первый, второй, третий.
Таким образом, в основе формирования понятия числа, с одной стороны, лежит счет предметов, который служит для определения их количества. Число выступает как результат счета и характеризует количество предметов данного множества («количественное число»).
С другой стороны, число как общая характеристика класса эквивалентных множеств осознается ребенком в процессе установления взаимно-однозначного соответствия между элементами различных множеств. Ответы на вопросы: «Больше?», «Меньше?», «Столько же?» — могут быть получены как способом пересчитывания, так и способом установления взаимно-однозначного соответствия. Эти способы используются параллельно, дополняя друг друга. Каждое число, называемое в процессе счета, ставится в соответствие одному из пересчитываемых предметов, характеризуя его порядок при счете («порядковое число»). Порядковая и количественная характеристика числа тесно связаны.
Овладение учащимися операцией счета предполагает усвоение порядка слов-числительных, используемого при счете, и определенных правил: первым при счете может быть указан любой объект данной совокупности, важно только, чтобы ему соответствовало числительное «один»; ни одному объекту нельзя поставить в соответствие два слова — числительных; ни один объект не должен быть пропущен при счете.
В большинстве программ раскрывается теоретико–множественный и аксиоматический смысл натурального числа. У с соавторами теоретико-множественный смысл: учащимся предлагаются задания связанные с установлением взаимно-однозначного соответствия между предметами различных групп. Число как название определённого количества. Аксиоматический: рассматривается вместе с теор.-множ. Связан с понятием отрезок ряда натуральных чисел.
Впервые дети получают представление о натуральном числе (у Моро) при определении темы «Числа от 1 до 10» с теор.-множ. и аксиом. смысла.
У подход примечателен тем, что рассматривается на примере однозначных чисел вообще смысл натурального числа, у детей складывается эмпирическое обобщение.
Развивающее обучение по системе Эльконина-Давыдова, авторский коллектив во главе с Давыдовым, раскрывают в своём учебнике натуральное число как результат измерения величины и в аксиоматическом смысле, с теоретико-множественного смысла раскрывается не специально при счёте количества.
33.2 Круг детского чтения рассчитан на пополнение литературного кругозора детей, повышения их начитанности. Сегодня поэзия и проза воспринимается как неотъемлемая часть круга детского чтения, с произведениями великого поэта читатели знакомятся едва ли не в самом раннем возрасте, они включены в школьную программу и сопровождают юного читателя в течение многих лет его взросления. Между тем изначально его стихотворения, повести, сказки не были написаны специально для детей и не рассматривались как произведения детской литературы. В то же время трудно переоценить значение пушкинских творений для формирующейся личности: они открывают маленькому читателю огромный мир человеческих мыслей, чувств, переживаний, приобщают его к общечеловеческим культурным ценностям и богатству родного языка; первое издание непосредственно для детей появилось только в начале ХХ века: в 1913 г. в Петербурге вышла в свет книга, которая так и называлась — «Пушкин для детей». Составители включили в неё около ста произведений: стихотворения, сказки, отрывки из поэм, повестей, пьес, отобрав из огромного пушкинского наследия то, что доступно и важно для детей среднего возраста.Творчество величайшего русского национального поэта необычайно расширило круг детского чтения и оказало огромное влияние на развитие литературы. Помимо сказок, детям можно отрывки из некоторых поэм Пушкина, как, например, в «Руслане и Людмиле» эпизоды быта, о поле, покрытом мертвыми костями, о богатырской голове; в «Полтаве» описание битвы, появление Петра Великого; наконец, некоторые из мелких стихотворений Пушкина, каковы: «Песнь о вещем Олеге», «Жених», «Пир Петра Великого», «Зимний вечер», «Утопленник», «Бесы», некоторые из «Песен западных славян».Первыми в круг детского чтения, как правило, входят сказки Пушкина. Чуть позже дети знакомятся с образцами пушкинской лирики. Это стихотворения самой разнообразной тематики: о природе, о дружбе и любви, об истории Родины и т. д. Т. о. сказки Пушкина привлекают внимание детей динамичным сюжетом, необычными ситуациями и событиями, сценами, полными чудес и роскоши. И так как каждая деталь в них естественна, реальна, тесно связана с жизнью или взята из мира, окружающего ребенка, то они легко воспринимаются, и в то же время вызывают удивление, воспитывают благородные чувства.
Хотя Пушкин не писал для детей, но история русской детской литературы немыслима без его произведений, а русское общество – без их воспитательного воздействия. Распространенное мнение, что Пушкин не писал для детей только потому, что ничего общего не хотел иметь с низкопробной детской литературой того времени, вряд ли является ответом на вопрос. Универсальный гений великого поэта, видевшего окружающий мир единым, не умещается ни в какие узкие рамки. Так же видел он и читателей, не разделяя их на возрастные группы. Как поэт Пушкин стремился быть доступным читателям всех возрастов, о чем прямо заявил еще в начале творческого пути. Я хочу, чтоб меня поняли все от мала до великого, – говорил 15-летний лицеист». И этому правилу следовал в течение всей своей творческой жизни.
35.1 Мышление — опосредованное и обобщенное отражение существенных, закономерных взаимосвязей действительности.
Мышление, являясь идеальным отражением действительности, имеет материальную форму своего проявления. Механизмом мышления человека является скрытая, беззвучная, внутренняя речь. Она характеризуется скрытой, незаметной для человека артикуляцией слов, микродвижениями органов речи.
Формами мышления являются: 1) суждение; 2) умозаключение; 3) понятие. Закономерности взаимоотношений между этими формами мышления изучает логика. Изучая формы мышления, логика отвлекается от конкретного содержания мыслей, заключенных в этих формах, она устанавливает общие законы и принципы достижения инстинности тех знаний, которые выводятся из других достоверных знаний. Психология же изучает закономерности творческого мышления, приводящего к новым познавательным результатам, к открытию новых знаний.
По преимущественному содержанию мыслительная деятельность подразделяется на: 1) практическую; 2) художественную и 3) научную.
Структурной единицей практического мышления является действие, а коммуникативной единицей — сигнал. В художественном мышлении структурной единицей является образ, а коммуникативной единицей — символ. В научном мышлении соответственно — понятие и знак.
В историческом развитии мышления и в развитии мышления ребенка различаются три сменяющие друг друга стадии — виды мышления: 1) наглядно-действенное (сенсомоторное); 2) наглядно-образное; 3) абстрактно-теоретическое.
Логические ОПЕРАЦИИ МЫШЛЕНИЯ — умственные действия над воспринимаемыми предметами, знаниями, образами, переживаниями. Важнейшими операциями мышления являются: анализ, синтез, сравнение, абстракция, обобщение, конкретизация, классификация и систематизация. Анализ — мысленное расчленение предмета, явления. Синтез — объединение частей, элементов в единое целое. Анализ и синтез — важнейшие мыслительные операции. Анализ дает знание отдельных элементов предмета, явления, а синтез, опираясь на результаты анализа, объединяя эти элементы, обеспечивает знание объекта, явления в целом. Сравнение — установление сходства и различия между объектами. Абстракция — отвлечение от каких-либо признаков явления, предмета. Благодаря абстракции возможно выделение существенных свойств и признаков предметов, явлений. Качества ума.
а) Глубина мысли, т. е. умение проникнуть в сущность труднейших вопросов теории и практики, разобраться в них, понять причины явлений, предвидеть дальнейший ход событий.
б) Широта мысли, заключающаяся в способности охватить вопрос в целом, когда не только вникают в существо данного дела, но и думают о том, что с ним связано, и в то же время не упускают из виду детали процесса или явления.
в) Гибкость ума, т. е. умение пересматривать свои выводы и решения в зависимости от изменившихся условий, отсутствие трафаретов в решении задачи, предвзятых мнений.
г) Критичность ума, т. е. умение не принимать на веру любое положение, а подвергать его критическому рассмотрению, и лишь после этого соглашаться с определенным положением или отвергать его.
Обучаемость- систему интеллектуальных свойств личности, формирующихся качеств ума, от которых зависит продуктивность учебной деятельности. Чем выше обучаемость, тем быстрее и легче приобретает человек новые знания, тем свободнее оперирует ими в относительно новых условиях, тем выше темп его умственного развития. Уровень и специфика обучаемости определяются формирующими качествами ума, каждое из которых имеет себе противоположное. В результате ряда современных исследовании выяснилось, что умственные возможности ребенка шире, чем предполагалось ранее, и при создании условий, т. е. при специальной методической организации обучения, младший школьник может усваивать абстрактный, теоретический материал. Особенно это проявляется на уроках математики, где от действий с конкретными предметами ученик переходит к умственным операциям с числом; то же имеет место и на уроках русского языка при усвоении учащимися слова, которое сначала не отделяется ими от предмета, но постепенно становится предметом специального изучения.
36.1 Мышление и речь. Многие ученые придерживаются компромиссной точки зрения, считая, что, хотя мышление и речь неразрывно связаны, они представляют собой как по генезису, так и по функционированию относительно независимые реальности. Значительный вклад в решение этой проблемы внес . Слово, писал он, так же относится к речи, как и к мышлению. Оно представляет собой живую клеточку, содержащую в самом простом виде основные свойства, присущие речевому мышлению в целом. Оно всегда характеризует предмет или явление, обозначаемое им, обобщенно и, следовательно, выступает как акт мышления. Но слово — это также средство общения, поэтому оно входит в состав речи. Однако мышление и речь имеют разные генетические корни. Первоначально они выполняли различные функции и развивались отдельно. Исходной функцией речи была коммуникативная функция. Сама речь как средство общения возникла в силу необходимости разделения и координации действий людей в процессе совместного труда. Вместе с тем при словесном общении содержание, передаваемое речью, относится к определенному классу явлений и, следовательно, уже тем самым предполагает их обобщенное отражение, т. е. факт мышления. В свою очередь, есть виды мышления, которые не связаны с речью, например наглядно-действенное, или практическое, мышление у животных. У маленьких детей и у высших животных обнаруживаются своеобразные средства коммуникации, не связанные с мышлением. Это выразительные движения, жесты, мимика, отражающие внутренние состояния живого существа, но не являющиеся знаком или обобщением.
Эгоцентрическая речь — это речь-размышление, обслуживающая не столько общение, сколько само мышление. Она выступает как внешняя по форме и внутренняя по своей психологической функции. Имея свои исходные корни во внешней диалогической речи, она, в конечном счете, перерастает во внутреннюю. При переходе внешней речи во внутреннюю эгоцентрическая речь постепенно исчезает. На убывание ее внешних проявлений следует смотреть, считал , как на усиливающуюся абстракцию мысли от звуковой стороны речи, что свойственно речи внутренней.
РЕЧЬ сложившаяся исторически в процессе материальной преобразующей деятельности людей форма общения, опосредствонанная языком.
методическим условием развития речи учащихся является создание ситуаций, вызывающих у школьников потребности высказываний, желание и необходимость что-то высказать устно или письменно. методическим условием развития речи учащихся является тщательная подготовка материала для речевых упражнений (рассказов, сочинений и пр.), забота о том, чтобы речь детей была по-настоящему содержательной. методическим условием развития речи учащихся является создание широкой системы речевой деятельности: с одной стороны, восприятие хороших образцов речи, достаточно разнообразных и содержащих необходимый языковый материал, с другой — создание условий для собственных речевых высказываний, в которых школьник мог бы использовать все те средства языка, которыми он должен овладеть.
Язык усваивается ребенком в общении, в процессе речевой деятельности. Но этого недостаточно: стихийно усвоенная речь нередко бывает примитивна и неправильна. Есть ряд аспектов овладения речью, которые находятся в ведении школы.
Это, во-первых, усвоение литературной языковой нормы. Во-вторых, это усвоение навыков чтения и письма — важнейших речевых навыков, необходимых каждому члену современного общества. Третья задача школы — это совершенствование культуры речи учащихся, доведение ее до такого минимального уровня, ниже которого не должен остаться ни один школьник.
Зона ближайшего развития – это расстояние между уровнем актуального развития ребёнка, которое определяется с помощью задач, решаемых самостоятельно, и уровнем возможного развития, определяемым с помощью задач, решаемых под руководством взрослых и в сотрудничестве с более умными сотоварищами. Понятие введено в начале 1930-х гг. . Понятие «зона ближайшего развития» (ЗБР) — это следствие закона развития высших психических функций, оно опирается на другие важные положения о развитии (на гипотезу о системном и смысловом строении сознания, закон гетерохронности, опосредованный характер развития высших психических функций).
Источник