Способ уравнивания по методу наименьших квадратов

Метод наименьших квадратов

Начнем статью сразу с примера. У нас есть некие экспериментальные данные о значениях двух переменных – x и y . Занесем их в таблицу.

i = 1	i = 2	i = 3	i = 4	i = 5
x i	0	1	2	4	5
y i	2 , 1	2 , 4	2 , 6	2 , 8	3 , 0

После выравнивания получим функцию следующего вида: g ( x ) = x + 1 3 + 1 .

Мы можем аппроксимировать эти данные с помощью линейной зависимости y = a x + b , вычислив соответствующие параметры. Для этого нам нужно будет применить так называемый метод наименьших квадратов. Также потребуется сделать чертеж, чтобы проверить, какая линия будет лучше выравнивать экспериментальные данные.

В чем именно заключается МНК (метод наименьших квадратов)

Главное, что нам нужно сделать, – это найти такие коэффициенты линейной зависимости, при которых значение функции двух переменных F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 будет наименьшим. Иначе говоря, при определенных значениях a и b сумма квадратов отклонений представленных данных от получившейся прямой будет иметь минимальное значение. В этом и состоит смысл метода наименьших квадратов. Все, что нам надо сделать для решения примера – это найти экстремум функции двух переменных.

Как вывести формулы для вычисления коэффициентов

Для того чтобы вывести формулы для вычисления коэффициентов, нужно составить и решить систему уравнений с двумя переменными. Для этого мы вычисляем частные производные выражения F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 по a и b и приравниваем их к 0 .

δ F ( a , b ) δ a = 0 δ F ( a , b ) δ b = 0 ⇔ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i = 0 — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) = 0 ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + ∑ i = 1 n b = ∑ i = 1 n y i ⇔ a ∑ i = 1 n x i 2 + b ∑ i = 1 n x i = ∑ i = 1 n x i y i a ∑ i = 1 n x i + n b = ∑ i = 1 n y i

Для решения системы уравнений можно использовать любые методы, например, подстановку или метод Крамера. В результате у нас должны получиться формулы, с помощью которых вычисляются коэффициенты по методу наименьших квадратов.

n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n

Мы вычислили значения переменных, при который функция
F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 примет минимальное значение. В третьем пункте мы докажем, почему оно является именно таким.

Это и есть применение метода наименьших квадратов на практике. Его формула, которая применяется для поиска параметра a , включает в себя ∑ i = 1 n x i , ∑ i = 1 n y i , ∑ i = 1 n x i y i , ∑ i = 1 n x i 2 , а также параметр
n – им обозначено количество экспериментальных данных. Советуем вам вычислять каждую сумму отдельно. Значение коэффициента b вычисляется сразу после a .

Обратимся вновь к исходному примеру.

Здесь у нас n равен пяти. Чтобы было удобнее вычислять нужные суммы, входящие в формулы коэффициентов, заполним таблицу.

i = 1	i = 2	i = 3	i = 4	i = 5	∑ i = 1 5
x i	0	1	2	4	5	12
y i	2 , 1	2 , 4	2 , 6	2 , 8	3	12 , 9
x i y i	0	2 , 4	5 , 2	11 , 2	15	33 , 8
x i 2	0	1	4	16	25	46

Решение

Четвертая строка включает в себя данные, полученные при умножении значений из второй строки на значения третьей для каждого отдельного i . Пятая строка содержит данные из второй, возведенные в квадрат. В последнем столбце приводятся суммы значений отдельных строчек.

Воспользуемся методом наименьших квадратов, чтобы вычислить нужные нам коэффициенты a и b . Для этого подставим нужные значения из последнего столбца и подсчитаем суммы:

n ∑ i = 1 n x i y i — ∑ i = 1 n x i ∑ i = 1 n y i n ∑ i = 1 n — ∑ i = 1 n x i 2 b = ∑ i = 1 n y i — a ∑ i = 1 n x i n ⇒ a = 5 · 33 , 8 — 12 · 12 , 9 5 · 46 — 12 2 b = 12 , 9 — a · 12 5 ⇒ a ≈ 0 , 165 b ≈ 2 , 184

У нас получилось, что нужная аппроксимирующая прямая будет выглядеть как y = 0 , 165 x + 2 , 184 . Теперь нам надо определить, какая линия будет лучше аппроксимировать данные – g ( x ) = x + 1 3 + 1 или 0 , 165 x + 2 , 184 . Произведем оценку с помощью метода наименьших квадратов.

Чтобы вычислить погрешность, нам надо найти суммы квадратов отклонений данных от прямых σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 и σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 , минимальное значение будет соответствовать более подходящей линии.

σ 1 = ∑ i = 1 n ( y i — ( a x i + b i ) ) 2 = = ∑ i = 1 5 ( y i — ( 0 , 165 x i + 2 , 184 ) ) 2 ≈ 0 , 019 σ 2 = ∑ i = 1 n ( y i — g ( x i ) ) 2 = = ∑ i = 1 5 ( y i — ( x i + 1 3 + 1 ) ) 2 ≈ 0 , 096

Ответ: поскольку σ 1 σ 2 , то прямой, наилучшим образом аппроксимирующей исходные данные, будет
y = 0 , 165 x + 2 , 184 .

Как изобразить МНК на графике функций

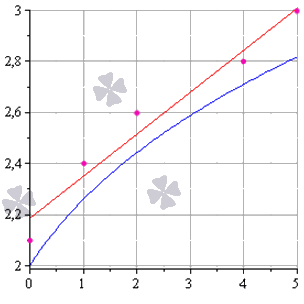
Метод наименьших квадратов наглядно показан на графической иллюстрации. С помощью красной линии отмечена прямая g ( x ) = x + 1 3 + 1 , синей – y = 0 , 165 x + 2 , 184 . Исходные данные обозначены розовыми точками.

Поясним, для чего именно нужны приближения подобного вида.

Они могут быть использованы в задачах, требующих сглаживания данных, а также в тех, где данные надо интерполировать или экстраполировать. Например, в задаче, разобранной выше, можно было бы найти значение наблюдаемой величины y при x = 3 или при x = 6 . Таким примерам мы посвятили отдельную статью.

Доказательство метода МНК

Чтобы функция приняла минимальное значение при вычисленных a и b , нужно, чтобы в данной точке матрица квадратичной формы дифференциала функции вида F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 была положительно определенной. Покажем, как это должно выглядеть.

У нас есть дифференциал второго порядка следующего вида:

d 2 F ( a ; b ) = δ 2 F ( a ; b ) δ a 2 d 2 a + 2 δ 2 F ( a ; b ) δ a δ b d a d b + δ 2 F ( a ; b ) δ b 2 d 2 b

Решение

δ 2 F ( a ; b ) δ a 2 = δ δ F ( a ; b ) δ a δ a = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ a = 2 ∑ i = 1 n ( x i ) 2 δ 2 F ( a ; b ) δ a δ b = δ δ F ( a ; b ) δ a δ b = = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) x i δ b = 2 ∑ i = 1 n x i δ 2 F ( a ; b ) δ b 2 = δ δ F ( a ; b ) δ b δ b = δ — 2 ∑ i = 1 n ( y i — ( a x i + b ) ) δ b = 2 ∑ i = 1 n ( 1 ) = 2 n

Иначе говоря, можно записать так: d 2 F ( a ; b ) = 2 ∑ i = 1 n ( x i ) 2 d 2 a + 2 · 2 ∑ x i i = 1 n d a d b + ( 2 n ) d 2 b .

Мы получили матрицу квадратичной формы вида M = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n .

В этом случае значения отдельных элементов не будут меняться в зависимости от a и b . Является ли эта матрица положительно определенной? Чтобы ответить на этот вопрос, проверим, являются ли ее угловые миноры положительными.

Вычисляем угловой минор первого порядка: 2 ∑ i = 1 n ( x i ) 2 > 0 . Поскольку точки x i не совпадают, то неравенство является строгим. Будем иметь это в виду при дальнейших расчетах.

Вычисляем угловой минор второго порядка:

d e t ( M ) = 2 ∑ i = 1 n ( x i ) 2 2 ∑ i = 1 n x i 2 ∑ i = 1 n x i 2 n = 4 n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2

После этого переходим к доказательству неравенства n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 с помощью математической индукции.

1. Проверим, будет ли данное неравенство справедливым при произвольном n . Возьмем 2 и подсчитаем:

2 ∑ i = 1 2 ( x i ) 2 — ∑ i = 1 2 x i 2 = 2 x 1 2 + x 2 2 — x 1 + x 2 2 = = x 1 2 — 2 x 1 x 2 + x 2 2 = x 1 + x 2 2 > 0

У нас получилось верное равенство (если значения x 1 и x 2 не будут совпадать).

1. Сделаем предположение, что данное неравенство будет верным для n , т.е. n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 – справедливо.
2. Теперь докажем справедливость при n + 1 , т.е. что ( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 > 0 , если верно n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 > 0 .

( n + 1 ) ∑ i = 1 n + 1 ( x i ) 2 — ∑ i = 1 n + 1 x i 2 = = ( n + 1 ) ∑ i = 1 n ( x i ) 2 + x n + 1 2 — ∑ i = 1 n x i + x n + 1 2 = = n ∑ i = 1 n ( x i ) 2 + n · x n + 1 2 + ∑ i = 1 n ( x i ) 2 + x n + 1 2 — — ∑ i = 1 n x i 2 + 2 x n + 1 ∑ i = 1 n x i + x n + 1 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + n · x n + 1 2 — x n + 1 ∑ i = 1 n x i + ∑ i = 1 n ( x i ) 2 = = ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + x n + 1 2 — 2 x n + 1 x 1 + x 1 2 + + x n + 1 2 — 2 x n + 1 x 2 + x 2 2 + . . . + x n + 1 2 — 2 x n + 1 x 1 + x n 2 = = n ∑ i = 1 n ( x i ) 2 — ∑ i = 1 n x i 2 + + ( x n + 1 — x 1 ) 2 + ( x n + 1 — x 2 ) 2 + . . . + ( x n — 1 — x n ) 2 > 0

Выражение, заключенное в фигурные скобки, будет больше 0 (исходя из того, что мы предполагали в пункте 2 ), и остальные слагаемые будут больше 0 , поскольку все они являются квадратами чисел. Мы доказали неравенство.

Ответ: найденные a и b будут соответствовать наименьшему значению функции F ( a , b ) = ∑ i = 1 n ( y i — ( a x i + b ) ) 2 , значит, они являются искомыми параметрами метода наименьших квадратов (МНК).

Источник

Решения задач: метод наименьших квадратов

Метод наименьших квадратов применяется для решения различных математических задач и основан на минимизации суммы квадратов отклонений функций от исходных переменных. Мы рассмотриваем его приложение к математической статистике в простейшем случае, когда нужно найти зависимость (парную линейную регрессию) между двумя переменными, заданными выборочными данным. В этом случае речь идет об отклонениях теоретических значений от экспериментальных.

Краткая инструкция по методу наименьших квадратов для чайников: определяем вид предполагаемой зависимости (чаще всего берется линейная регрессия вида $y(x)=ax+b$), выписываем систему уравнений для нахождения параметров $a, b$. По экспериментальным данным проводим вычисления и подставляем значения в систему, решаем систему любым удобным методом (для размерности 2-3 можно и вручную). Получается искомое уравнение.

Иногда дополнительно к нахождению уравнения регрессии требуется: найти остаточную дисперсию, сделать прогноз значений, найти значение коэффициента корреляции, проверить качество аппроксимации и значимость модели. Примеры решений вы найдете ниже. Удачи в изучении!

Примеры решений МНК

Пример 1. Методом наименьших квадратов для данных, представленных в таблице, найти линейную зависимость

Пример 2. Прибыль фирмы за некоторый период деятельности по годам приведена ниже:
Год 1 2 3 4 5
Прибыль 3,9 4,9 3,4 1,4 1,9
1) Составьте линейную зависимость прибыли по годам деятельности фирмы.
2) Определите ожидаемую прибыль для 6-го года деятельности. Сделайте чертеж.

Пример 3. Экспериментальные данные о значениях переменных х и y приведены в таблице:
1 2 4 6 8
3 2 1 0,5 0
В результате их выравнивания получена функция Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.

Пример 4. Данные наблюдений над случайной двумерной величиной (Х, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X.

Пример 5. Считая, что зависимость между переменными x и y имеет вид $y=ax^2+bx+c$, найти оценки параметров a, b и c методом наименьших квадратов по выборке:
x 7 31 61 99 129 178 209
y 13 10 9 10 12 20 26

Пример 6. Проводится анализ взаимосвязи количества населения (X) и количества практикующих врачей (Y) в регионе.
Годы 81 82 83 84 85 86 87 88 89 90
X, млн. чел. 10 10,3 10,4 10,55 10,6 10,7 10,75 10,9 10,9 11
Y, тыс. чел. 12,1 12,6 13 13,8 14,9 16 18 20 21 22
Оцените по МНК коэффициенты линейного уравнения регрессии $y=b_0+b_1x$.
Существенно ли отличаются от нуля найденные коэффициенты?
Проверьте значимость полученного уравнения при $\alpha = 0,01$.
Если количество населения в 1995 году составит 11,5 млн. чел., каково ожидаемое количество врачей? Рассчитайте 99%-й доверительный интервал для данного прогноза.
Рассчитайте коэффициент детерминации

Источник

Глава 3 Оценка параметров

Цель любого физического эксперимента — проверить, выполняется ли некоторая теоретическая закономерность ( модель ), а также получить или уточнить её параметры. Поскольку набор экспериментальных данных неизбежно ограничен, а каждое отдельное измерение имеет погрешность, можно говорить лишь об оценке этих параметров. В большинстве случаев измеряется не одна величина, а некоторая функциональная зависимость величин друг от друга. В таком случае возникает необходимость построить оценку параметров этой зависимости.

Пример. Рассмотрим процедуру измерения сопротивления некоторого резистора. Простейшая теоретическая модель для резистора — закон Ома U = R ⁢ I , где сопротивление R — единственный параметр модели. Часто при измерениях возможно возникновение систематической ошибки — смещение нуля напряжения или тока. Тогда для получения более корректной оценки сопротивления стоит использовать модель с двумя параметрами: U = R ⁢ I + U 0 .

Для построения оценки нужны следующие компоненты

данные — результаты измерений < x i , y i >и их погрешности < σ i >(экспериментальная погрешность является неотъемлемой частью набора данных!);

модель y = f ⁢ ( x | θ 1 , θ 2 , … ) — параметрическое описание исследуемой зависимости ( θ — набор параметров модели, например, коэффициенты < k , b >прямой f ⁢ ( x ) = k ⁢ x + b );

процедура построения оценки параметров по измеренным данным («оценщик»):

Рассмотрим самые распространенные способы построения оценки.

3.1 Метод минимума хи-квадрат

Обозначим отклонения результатов некоторой серии измерений от теоретической модели y = f ⁢ ( x | θ ) как

Δ ⁢ y i = y i — f ⁢ ( x i | θ ) , i = 1 ⁢ … ⁢ n ,

где θ — некоторый параметр (или набор параметров), для которого требуется построить наилучшую оценку. Нормируем Δ ⁢ y i на стандартные отклонения σ i и построим сумму

χ 2 = ∑ i ( Δ ⁢ y i σ i ) 2 ,

(3.1)

которую принято называть суммой хи-квадрат .

Метод минимума хи-квадрат ( метод Пирсона ) заключается в подборе такого θ , при котором сумма квадратов отклонений от теоретической модели, нормированных на ошибки измерений, достигает минимума:

χ 2 ⁢ ( θ ) → min .

Замечание. Подразумевается, что погрешность измерений σ i указана только для вертикальной оси y . Поэтому, при использовании метода следует выбирать оcи таким образом, чтобы относительная ошибка по оси абсцисс была значительно меньше, чем по оси ординат.

Данный метод вполне соответствует нашему интуитивному представлению о том, как теоретическая зависимость должна проходить через экспериментальные точки. Ясно, что чем ближе данные к модельной кривой, тем меньше будет сумма χ 2 . При этом, чем больше погрешность точки, тем в большей степени дозволено результатам измерений отклоняться от модели. Метода минимума χ 2 является частным случаем более общего метода максимума правдоподобия (см. ниже), реализующийся при нормальном ( гауссовом ) распределении ошибок.

Можно показать (см. [ 5 ] ), что оценка по методу хи-квадрат является состоятельной, несмещенной и, если данные распределены нормально, имеет максимальную эффективность (см. приложение 5.2 ).

Замечание. Простые аналитические выражения для оценки методом хи-квадрат существуют (см. п. 3.6.1 , 3.6.4 ) только в случае линейной зависимости f ⁢ ( x ) = k ⁢ x + b (впрочем, нелинейную зависимость часто можно заменой переменных свести к линейной). В общем случае задача поиска минимума χ 2 ⁢ ( θ ) решается численно, а соответствующая процедура реализована в большинстве специализированных программных пакетов по обработке данных.

3.2 Метод максимального правдоподобия.

Рассмотрим кратко один из наиболее общих методов оценки параметров зависимостей — метод максимума правдоподобия.

Сделаем два ключевых предположения:

зависимость между измеряемыми величинами действительно может быть описана функцией y = f ⁢ ( x | θ ) при некотором θ ;

все отклонения Δ ⁢ y i результатов измерений от теоретической модели являются независимыми и имеют случайный (не систематический!) характер.

Пусть P ⁢ ( Δ ⁢ y i ) — вероятность обнаружить отклонение Δ ⁢ y i при фиксированных < x i >, погрешностях < σ i >и параметрах модели θ . Построим функцию, равную вероятности обнаружить весь набор отклонений < Δ ⁢ y 1 , … , Δ ⁢ y n >. Ввиду независимости измерений она равна произведению вероятностей:

L = ∏ i = 1 n P ⁢ ( Δ ⁢ y i ) .

(3.2)

Функцию L называют функцией правдоподобия .

Метод максимума правдоподобия заключается в поиске такого θ , при котором наблюдаемое отклонение от модели будет иметь наибольшую вероятность , то есть

L ⁢ ( θ ) → max .

Пусть теперь ошибки измерений имеют нормальное распределение (напомним, что согласно центральной предельной теореме нормальное распределение применимо, если отклонения возникают из-за большого числа независимых факторов, что на практике реализуется довольно часто). Согласно ( 2.5 ), вероятность обнаружить в i -м измерении отклонение Δ ⁢ y i пропорциональна величине

P ⁢ ( Δ ⁢ y i ) ∝ e — Δ ⁢ y i 2 2 ⁢ σ i 2 ,

где σ i — стандартная ошибка измерения величины y i . Тогда логарифм функции правдоподобия ( 3.2 ) будет равен (с точностью до константы)

ln ⁡ L = — ∑ i Δ ⁢ y i 2 2 ⁢ σ i 2 = — 1 2 ⁢ χ 2 .

Таким образом, максимум правдоподобия действительно будет соответствовать минимуму χ 2 .

3.3 Метод наименьших квадратов (МНК).

Рассмотрим случай, когда все погрешности измерений одинаковы, σ i = const . Тогда множитель 1 / σ 2 в сумме χ 2 выносится за скобки, и оценка параметра сводится к нахождению минимума суммы квадратов отклонений:

S ⁢ ( θ ) = ∑ i = 1 n ( y i — f ⁢ ( x i | θ ) ) 2 → min .

(3.3)

Оценка по методу наименьших квадратов (МНК) удобна в том случае, когда не известны погрешности отдельных измерений. Однако тот факт, что метод МНК игнорирует информацию о погрешностях, является и его основным недостатком. В частности, это не позволяет определить точность оценки (например, погрешности коэффициентов прямой σ k и σ b ) без привлечения дополнительных предположений (см. п. 3.6.2 и 3.6.3 ).

3.4 Проверка качества аппроксимации

Значение суммы χ 2 позволяет оценить, насколько хорошо данные описываются предлагаемой моделью y = f ⁢ ( x | θ ) .

Предположим, что распределение ошибок при измерениях нормальное . Тогда можно ожидать, что большая часть отклонений данных от модели будет порядка одной среднеквадратичной ошибки: Δ ⁢ y i ∼ σ i . Следовательно, сумма хи-квадрат ( 3.1 ) окажется по порядку величины равна числу входящих в неё слагаемых: χ 2 ∼ n .

Замечание. Точнее, если функция f ⁢ ( x | θ 1 , … , θ p ) содержит p подгоночных параметров (например, p = 2 для линейной зависимости f ⁢ ( x ) = k ⁢ x + b ), то при заданных θ лишь n — p слагаемых в сумме хи-квадрат будут независимы. Иными словами, когда параметры θ определены из условия минимума хи-квадрат, сумму χ 2 можно рассматривать как функцию n — p переменных. Величину n — p называют числом степеней свободы задачи.

В теории вероятностей доказывается (см. [ 4 ] или [ 5 ] ), что ожидаемое среднее значение (математическое ожидание) суммы χ 2 в точности равно числу степеней свободы:

χ 2 ¯ = n — p .

Таким образом, при хорошем соответствии модели и данных, величина χ 2 / ( n — p ) должна в среднем быть равна единице. Значения существенно большие (2 и выше) свидетельствуют либо о плохом соответствии теории и результатов измерений , либо о заниженных погрешностях . Значения меньше 0,5 как правило свидетельствуют о завышенных погрешностях .

Замечание. Чтобы дать строгий количественный критерий, с какой долей вероятности гипотезу y = f ⁢ ( x ) можно считать подтверждённой или опровергнутой, нужно знать вероятностный закон, которому подчиняется функция χ 2 . Если ошибки измерений распределены нормально, величина хи-квадрат подчинятся одноимённому распределению (с n — p степенями свободы). В элементарных функциях распределение хи-квадрат не выражается, но может быть легко найдено численно: функция встроена во все основные статистические пакеты, либо может быть вычислена по таблицам.

3.5 Оценка погрешности параметров

Важным свойством метода хи-квадрат является «встроенная» возможность нахождения погрешности вычисленных параметров σ θ .

Пусть функция L ⁢ ( θ ) имеет максимум при θ = θ ^ , то есть θ ^ — решение задачи о максимуме правдоподобия. Согласно центральной предельной теореме мы ожидаем, что функция правдоподобия будем близка к нормальному распределению: L ⁢ ( θ ) ∝ exp ⁡ ( — ( θ — θ ^ ) 2 2 ⁢ σ θ 2 ) , где σ θ — искомая погрешность параметра. Тогда в окрестности θ ^ функция χ 2 ⁢ ( θ ) = — 2 ⁢ ln ⁡ ( L ⁢ ( θ ) ) имеет вид параболы:

χ 2 ⁢ ( θ ) = ( θ — θ ^ ) 2 σ θ 2 + const .

Легко убедиться, что:

χ 2 ⁢ ( θ ^ ± σ θ ) — χ 2 ⁢ ( θ ^ ) = 1 .

Иными словами, при отклонении параметра θ на одну ошибку σ θ от значения θ ^ , минимизирующего χ 2 , функция χ 2 ⁢ ( θ ) изменится на единицу. Таким образом для нахождения интервальной оценки для искомого параметра достаточно графическим или численным образом решить уравнение

Δ ⁢ χ 2 ⁢ ( θ ) = 1 .

(3.4)

Вероятностное содержание этого интервала будет равно 68% (его еще называют 1– σ интервалом). Отклонение χ 2 на 2 будет соответствовать уже 95% доверительному интервалу.

Замечание. Приведенное решение просто использовать только в случае одного параметра. Впрочем, все приведенные рассуждения верны и в много-параметрическом случае. Просто решением уравнения 3.4 будет не отрезок, а некоторая многомерная фигура (эллипс в двумерном случае и гипер-эллипс при больших размерностях пространства параметров). Вероятностное содержание области, ограниченной такой фигурой будет уже не равно 68%, но может быть вычислено по соответствующим таблицам. Подробнее о многомерном случае в разделе 5.5 .

3.6 Методы построения наилучшей прямой

Применим перечисленные выше методы к задаче о построении наилучшей прямой y = k ⁢ x + b по экспериментальным точкам < x i , y i >. Линейность функции позволяет записать решение в относительно простом аналитическом виде.

Обозначим расстояние от i -й экспериментальной точки до искомой прямой, измеренное по вертикали, как

Δ ⁢ y i = y i — ( k ⁢ x i + b ) ,

и найдём такие параметры < k , b >, чтобы «совокупное» отклонение результатов от линейной зависимости было в некотором смысле минимально.

3.6.1 Метод наименьших квадратов

Пусть сумма квадратов расстояний от точек до прямой минимальна:

S ⁢ ( k , b ) = ∑ i = 1 n ( y i — ( k ⁢ x i + b ) ) 2 → min .

(3.5)

Данный метод построения наилучшей прямой называют методом наименьших квадратов (МНК).

Рассмотрим сперва более простой частный случай, когда искомая прямая заведомо проходит через «ноль», то есть b = 0 и y = k ⁢ x . Необходимое условие минимума функции S ⁢ ( k ) , как известно, есть равенство нулю её производной. Дифференцируя сумму ( 3.5 ) по k , считая все величины < x i , y i >константами, найдём

d ⁢ S d ⁢ k = — ∑ i = 1 n 2 ⁢ x i ⁢ ( y i — k ⁢ x i ) = 0 .

Решая относительно k , находим

k = ∑ i = 1 n x i ⁢ y i ∑ i = 1 n x i 2 .

Поделив числитель и знаменатель на n , этот результат можно записать более компактно:

k = ⟨ x ⁢ y ⟩ ⟨ x 2 ⟩ .

(3.6)

Напомним, что угловые скобки означают усреднение по всем экспериментальным точкам:

⟨ … ⟩ ≡ 1 n ⁢ ∑ i = 1 n ( … ) i

В общем случае при b ≠ 0 функция S ⁢ ( k , b ) должна иметь минимум как по k , так и по b . Поэтому имеем систему из двух уравнений ∂ ⁡ S / ∂ ⁡ k = 0 , ∂ ⁡ S / ∂ ⁡ b = 0 , решая которую, можно получить (получите самостоятельно):

-\left \left ><\left -\left% ^<2>>,\qquad b=\left -k\left .» display=»block»> k = ⟨ x ⁢ y ⟩ — ⟨ x ⟩ ⁢ ⟨ y ⟩ ⟨ x 2 ⟩ — ⟨ x ⟩ 2 , b = ⟨ y ⟩ — k ⁢ ⟨ x ⟩ .

(3.7)

Эти соотношения и есть решение задачи о построении наилучшей прямой методом наименьших квадратов.

3.6.2 Погрешность МНК в линейной модели

Погрешности σ k и σ b коэффициентов, вычисленных по формуле ( 3.7 ) (или ( 3.6 )), можно оценить в следующих предположениях. Пусть погрешность измерений величины x пренебрежимо мала: σ x ≈ 0 , а погрешности по y одинаковы для всех экспериментальных точек σ y = const , независимы и имеют случайный характер (систематическая погрешность отсутствует).

Пользуясь в этих предположениях формулами для погрешностей косвенных измерений (см. раздел ( 2.6 )) можно получить следующие соотношения:

σ k = 1 n — 2 ⁢ ( D y ⁢ y D x ⁢ x — k 2 ) ,

(3.10)

σ b = σ k ⁢ ⟨ x 2 ⟩ ,

(3.11)

где использованы введённые выше сокращённые обозначения ( 3.8 ). Коэффициент n — 2 отражает число независимых >: n экспериментальных точек за вычетом двух условий связи ( 3.7 ).

В частном случае y = k ⁢ x :

σ k = 1 n — 1 ⁢ ( ⟨ y 2 ⟩ ⟨ x 2 ⟩ — k 2 ) .

(3.12)

3.6.3 Недостатки и условия применимости МНК

Формулы ( 3.7 ) (или ( 3.6 )) позволяют провести прямую по любому набору экспериментальных данных, а полученные выше соотношения — вычислить соответствующую среднеквадратичную ошибку для её коэффициентов. Однако далеко не всегда результат будет иметь физический смысл. Перечислим ограничения применимости данного метода.

В первую очередь метод наименьших квадратов — статистический, и поэтому он предполагает использование достаточно большого количества экспериментальных точек (желательно 10″ display=»inline»> n > 10 ).

Поскольку метод предполагает наличие погрешностей только по y , оси следует выбирать так, чтобы погрешность σ x откладываемой по оси абсцисс величины была минимальна.

Кроме того, метод предполагает, что все погрешности в опыте — случайны. Соответственно, формулы ( 3.10 )–( 3.12 ) применимы только для оценки случайной составляющей ошибки k или b . Если в опыте предполагаются достаточно большие систематические ошибки, они должны быть оценены отдельно . Отметим, что для оценки систематических ошибок не существует строгих математических методов, поэтому в таком случае проще и разумнее всего воспользоваться графическим методом.

Одна из основных проблем, связанных с определением погрешностей методом наименьших квадратов заключается в том, что он дает разумные погрешности даже в том случае, когда данные вообще не соответствуют модели. Если погрешности измерений известны, предпочтительно использовать метод минимума χ 2 .

Наконец, стоит предостеречь от использования любых аналитических методов «вслепую», без построения графиков. В частности, МНК не способен выявить такие «аномалии», как отклонения от линейной зависимости, немонотонность, случайные всплески и т.п. Все эти случаи требуют особого рассмотрения и могут быть легко обнаружены визуально при построении графика.

3.6.4 Метод хи-квадрат построения прямой

Пусть справедливы те же предположения, что и для метода наименьших квадратов, но погрешности σ i экспериментальных точек различны. Метод минимума хи-квадрат сводится к минимизации суммы квадратов отклонений, где каждое слагаемое взято с весом w i = 1 / σ i 2 :

χ 2 ⁢ ( k , b ) = ∑ i = 1 n w i ⁢ ( y i — ( k ⁢ x i + b ) ) 2 → min .

Этот метод также называют взвешенным методом наименьших квадратов.

Определим взвешенное среднее от некоторого набора значений < x i >как

⟨ x ⟩ ′ = 1 W ⁢ ∑ i w i ⁢ x i ,

где W = ∑ i w i — нормировочная константа.

Повторяя процедуру, использованную при выводе ( 3.7 ), нетрудно получить (получите) совершенно аналогичные формулы для искомых коэффициентов:

^<\prime>-\left ^<\prime>\left ^<\prime% >><\left ^<\prime>-\left ^<\prime 2>>,\qquad b=\left ^<\prime>-k\left ^<\prime>,» display=»block»> k = ⟨ x ⁢ y ⟩ ′ — ⟨ x ⟩ ′ ⁢ ⟨ y ⟩ ′ ⟨ x 2 ⟩ ′ — ⟨ x ⟩ ′ ⁣ 2 , b = ⟨ y ⟩ ′ — k ⁢ ⟨ x ⟩ ′ ,

(3.13)

с тем отличием от ( 3.7 ), что под угловыми скобками ⟨ … ⟩ ′ теперь надо понимать усреднение с весами w i = 1 / σ i 2 .

Записанные формулы позволяют вычислить коэффициенты прямой, если известны погрешности σ y i . Значения σ y i могут быть получены либо из некоторой теории, либо измерены непосредственно (многократным повторением измерений при каждом x i ), либо оценены из каких-то дополнительных соображений (например, как инструментальная погрешность).

Источник