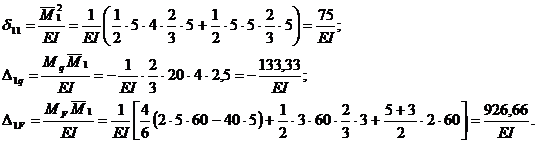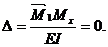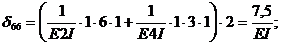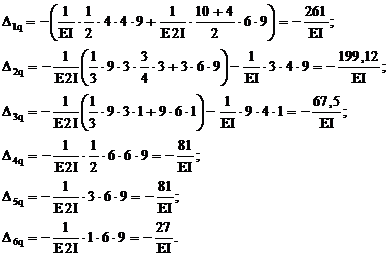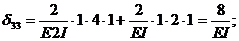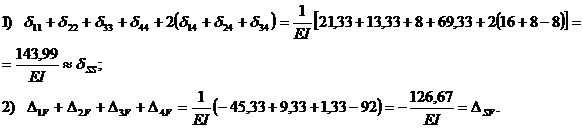Способ упрощения расчета симметричных рам методом сил

Содержание

Упрощения при расчете симметричных рам
Упрощения при расчете симметричных рам
Расчет симметричных систем методом сил

Упрощения при расчете симметричных рам

Упрощение при расчете симметричных рам, наиболее трудоемкой части расчета статических неопределенных систем силовым методом, можно добиться упрощения при расчете рам силовым методом только за счет нулевой инверсии расчета неизвестных боковых коэффициентов в основной системе перемещений от

одиночных и нагрузочных воздействий. Для фрейма произвольных геометрических фигур это может быть достигнуто путем выбора базовой системы, в которой участки из отдельных эффектов являются локальными, для этого система делится на геометрические инвариантные части, где все больше и больше

одиночных участков не имеют общих областей. При выборе этой базовой системы каждое Людмила Фирмаль

каноническое уравнение содержит неполное число неизвестных, что облегчает его вычисление. Можно добиться более существенного упрощения при расчете симметричных систем. Такие системы имеют симметричную геометрическую схему, в которой жесткость симметрично расположенных элементов равна друг другу. Чтобы упростить расчет симметричной рамки, нужно выбрать только

симметричную основную систему. 415 страниц. 34.12 В симметричной базовой системе, выбранной путем отбрасывания избыточной связи на оси симметрии, неизвестные X / силы делятся на две группы: симметричные и антисимметричные. Разделение неизвестных на две группы приводит к разделению общей системы нормальных уравнений на две подсистемы,одна из которых содержит только симметричные неизвестные. Рассмотрим симметричную

рамку(рис. 34.11, а). Этот кадр трижды статически неопределим. Выберем базовую систему симметрии, разрезав рамку по оси симметрии на две части(рис. 34.11). Поскольку в месте разреза удаляются три внутренних соединения, то его воздействие будет заменено тремя внутренними силами M, N и Q изгибающего момента на обеих половинах разрезаемой Рамы X-Y силами-X3 и поперечными продольными силами-X3(рис. 34.11, б). Запишите канонические уравнения трех статических неопределенных систем: PH1+612X2+61zhz+D1g=0;1 Шесть. Два. 1×1+»2 2+»2Z x z+D2=0g ; Е31+*32 *2+*33 X3+A3F=0. Дж Чтобы определить коэффициенты неизвестных,

создайте диаграмму сгиба в выбранной базовой системе От мощности блока 416моментов X>=1;x2=1 и XS=1(фиг. 34.11, г-е). На симметрично расположенных участках участков Mg и M2 вертикальные оси моментов равны друг другу, а знак совпадает друг с другом, поскольку в симметричной части вертикальные оси моментов равны друг другу, но знак противоположен. Таким образом,неизвестные Xi и x2 симметричны, в то время как X3 нехарактерно неизвестен. Таким образом, в симметричной базовой системе неизвестное

X/делится на симметричное и антисимметричное вместо разрушенного Людмила Фирмаль

внутреннего пространства по оси симметрии. Так как все участки Mi, M2, M3 линейны, то для определения коэффициентов неизвестного используем правила Верещагина. Умножьте [симметричный график M]на график обратной симметрии M3, чтобы указать, что боковое смещение BLZ равно нулю. Сначала умножьте левую сторону рамки на участки M<и M3, затем на правую сторону»!»3=» 31=S f ds («»•D/(2^A) — —(N•1)/(2G J2 2 * 2)+(lh•1)/(2EL)+ ‘ ll•1) I(2EJ2 2•2)=0. Аналогично, 623=632=0. Итак, от умножения симметричного участка по правилам Верещагина до антисимметричного участка соответствующее

перемещение (одиночное или грузовое) равно нулю. В нашем случае система нормальных уравнений принимает вид: n * 1-M12 * 2+D1£=0;| 621Xl+e22X2+A2F=0;)633 × 3+A3F=0 • То есть целостная система делится на две подсистемы. Для определения симметричных неизвестных (Xt и x2) необходимо решить систему из двух уравнений с двумя неизвестными, а антисимметричное неизвестное (X3) должно иметь одно неизвестное. 27-480 417: группа неизвестна. При вычислении сложных статически неопределенных фреймов не всегда удается разместить все неизвестные силы вместо разрушенных связей на оси симметрии, и в этом случае используется метод групповых

неизвестных для преобразования неизвестных в симметрии и антисимметрии. В качестве примера рассмотрим симметричную рамку(рис. 34.12, а). Этот кадр статически неопределим дважды. Отбросим стержни опор B и C и выберем базовую симметричную систему, заменив их неизвестными силами X\и X’2 (рис. 34.12, б). Поскольку силы X\и X’2 не равны друг другу, для вычисления заданного кадра необходимо решить систему двух канонических уравнений с двумя неизвестными, но для одной и той же базовой системы мы можем получить симметричный и антисимметричный график симметрии неизвестного момента от изгибающей силы. Для этого вместо одной силы применяется группа сил. Неизвестную реакцию\и Х2 в опоре представить суммой двух сил х, а неизвестну

ю реакцию в опоре с представить в виде разности между теми же силами х^и Х2(и ее 34.12, б). Это преобразование основано на известной теореме алгебры, согласно которой две неизвестные величины X’1 и X’2 могут быть заменены двумя другими неизвестными. После перехода к неизвестному числу групп, биссектрисная сила, приложенная к симметричному поперечному сечению каркаса XY, симметрична неизвестной, так как график изгибающего момента L4 от его одновременного действия,основной системы 34.12 g). Две другие силы x2 являются антисимметричными и неизвестными, поскольку из-за их одновременного действия график изгибающего момента M2 в основной системе является антисимметричным(рис. 34.12, г). Поскольку неизвестные Xi и x2

разделены на две группы, боковое смещение 612=621=0 равно нулю из графика симметрии, умноженного на обратную симметрию M2, а каноническая система уравнений равна: =0 и 622^2_| » D2/7=: = 0. 41N^X r l X,=t И ЗП ДХ Рис 34.14 I г Введение жесткой консоли. Иногда при расчете симметричной трехградусной неопределенной рамки, состоящей из одного замкнутого контура или имеющей U-образную форму, требуется полная система канонических уравнений для введения жесткой консоли. Чтобы проиллюстрировать этот метод, N-o-различные симметричные трехградусные статические неопределенные кадры(рис. 34.13, а). Попробуем выбрать основную систему симметрии, разрезав поперечину рамы вдоль оси симметрии на две части. Вместо того чтобы разрезать каждую часть поперечины, добавьте вертикальную жесткую консоль (£7=OO). Введение жестко

й консоли в основную систему не меняет характера распределения внутренних сил и деформаций в данной системе. Вместо этого приложите продольную силу Xj и боковую силу x2 к оси перекладины трех отброшенных звеньев. Вместо изгибающего момента, возникающего в режущей части ригеля, действует горизонтальная сила Х3 (рис. 34.13, 6). Эти силы заменяют моменты сечения, равные Hz (/o). В выбранной симметричной системе основания неизвестная сила была разделена на симметричную XY X3 и противоположную- Двадцать семь* 419nesymmetric Х2. Таким образом, канонические уравнения делятся на две группы \1x i+BZ x z+=°; 1\ + bzz X z+d Zr=0;/ 22 2 + D2R=°- Чтобы разделить систему симметрии канонического уравнения на два независимых уравнения, боковое смещение

B13=bz1=0 должно быть равно нулю. Боковое перемещение 6j3 будет равно нулю, если взять жесткую длину консоли, равную y0=2L / 3. В этом случае для центра тяжести участка изгибающего момента Mi нулевые координаты участка L43 размещаются на стойке (рис. В результате, 34.13, d)и 6i3=0, система нормальных уравнений для вычисления заданного кадра распадается на три независимых уравнения: +D1G=0$22X2+D2P=0, 633X3+D2g=0- Преобразование внешних нагрузок. Описанный способ упрощения расчета симметричной рамки заключается в том, что для разделения полной системы канонических уравнений на симметричную и антисимметричную подсистемы, при работе на симметричной рамке с неизвестной, но только симметричной нагрузкой, все члены

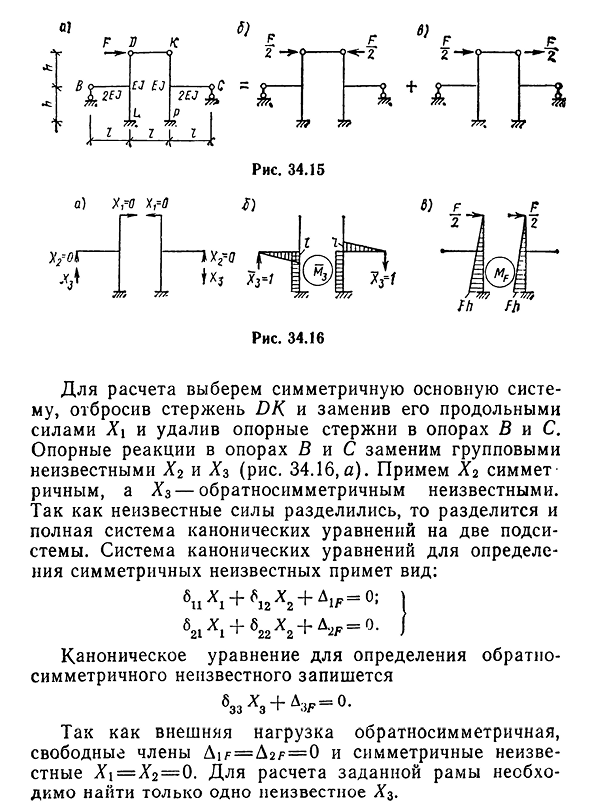
подсистемы обратной симметрии в каноническом уравнении свободного члена исчезают, а соответствующее неизвестное число равно этому уменьшает степень статической неопределенности рамки. Рассмотрим дважды статическую неопределенную рамку, нагруженную симметричной фокусирующей нагрузкой(рис. 34.14, а). Для расчета этой рамы выберите симметричную основную систему, разрезав ее шарнирами D на две части. Вместо отброшенного соединения с каждым компонентом, продольная сила Xi и поперечная сила x2(фиг. 34.14, 6). Поскольку неизвестное

расположено на оси симметрии, Xi симметрично,а x2-обратно. Каноническое уравнение делится на два независимых уравнения:6ixi+a i_f=^,&22X2+^2f=0. Изгибающий момент показан на рисунке и рисунке L4m2. 34.14, Б-6. 420 для определения свободных термов Aif и D2G соответствующий единичный участок следует умножить на участок от заданной нагрузки по правилам Верещагина:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Источник

Расчет симметричных систем методом сил

Использование метода сил для расчета систем с высокой степенью статической неопределимости связано с решением совместной системы большого количества линейных уравнений. Даже самый экономичных метод решения таких систем – алгоритм Гаусса – требует вычислительных операций (где n – число уравнений, т.е. степень статической неопределимости системы), при условии, что все коэффициенты системы отличны от нуля. В связи с этим нужно стремиться так выбрать основную систему, чтобы возможно большее число побочных единичных перемещений и свободных членов обратилось в ноль.

Основным средством для достижения этой цели является использование симметрии. Стержневая система является симметричной, если симметричны не только оси и опорные закрепления (геометрическая симметрия), но и жесткости (упругая симметрия). При этом внешняя нагрузка может быть и несимметричной.

При выборе основной системы лишние неизвестные следует выбирать в виде симметричных и обратно симметричных усилий. Симметричные неизвестные создают симметричные эпюры моментов, а обратно симметричные неизвестные – кососимметричные эпюры. Такие эпюры обладают свойством взаимной ортогональности, т.е. результат их перемножения равен нулю:

(3.14)

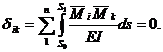
Ортогонализация эпюр может достигаться различными способами:

1) выбор симметричной основной системы; 2) выбор симметричных и обратносимметричных неизвестных; 3) группировка неизвестных; 4) устройство жестких консолей (способ упругого центра); 5) использование статически неопределимой основной системы; 6) разложение произвольной нагрузки на симметричную и обратносимметричную составляющие.

Использование большинства этих способов будет рассмотрено ниже на конкретных примерах, здесь же охарактеризуем только способ, заключающийся в применении статически неопределимой основной системы. Для расчета статически неопределимой системы можно отбрасывать не все лишние неизвестные, а одно или несколько. При этом уменьшается число канонических уравнений. Так, рассчитывая n раз статически неопределимую систему, можно не решать n уравнений, если в качестве основной системы применять систему со степенью статической неопределимости n -1. Для определения усилия в i-ой удаленной связи достаточно решить лишь одно уравнение:

где и — перемещения по направлению в основной, (n-1) раз статически неопределимой системе, вызываемые усилием и внешней нагрузкой соответственно.

Следовательно, рассматриваемый способ требует, чтобы предварительно были вычислены все необходимые перемещения в статически неопределимой основной системе. Для этого необходимо заранее иметь эпюры внутренних усилий от действия на статически неопределимую основную систему единичных неизвестных и заданной внешней нагрузки. Если же таких эпюр нет, то расчет не только не упростится, но даже может усложниться. Это обстоятельство резко ограничивает практическую область применения рассмотренного способа.

Примеры расчетов

Рассмотрим приведенный выше алгоритм расчета различных систем методом сил на конкретных примерах статически неопределимых балок и плоских рам.

Пример 18. Построить эпюру изгибающих моментов для статически неопределимой балки (рис.36,а).

Степень статической неопределимости балки:

Основная и эквивалентная система приведены на рис.36,б,в. Так выбор основной системы является наиболее рациональным, но не единственным. Можно было, например, заменить жесткую заделку на шарнирнонеподвижную опору; тогда основная система представляла бы собой статически определимую шарнирную балку, а лишняя неизвестная – сосредоточенный момент X, приложенный к левой опоре.

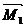
Эпюра изгибающих моментов от внешней нагрузки (рис.36,д) имеет размерность Кн·м, а единичная эпюра моментов (рис.36,ж) — м.

Каноническое уравнение метода сил:

Вычисляем коэффициенты и , перемножая соответствующие эпюры по правилу Верещагина:

Реакция лишней связи:

Таким образом, исходная статически неопределимая система, загруженная распределенной нагрузкой q, приведена к статически определимой системе (жестко защемленная балка), загруженной распределенной нагрузкой q и сосредоточенной силой (рис.36, з).

На рис.37,а,б представлены эпюры поперечных сил Q и изгибающих моментов для заданной системы.

Отметим, что эпюры Q и (рис.37) построены непосредственно методом сечений, причем по условиям задачи построение эпюры Q не является обязательным. Тем не менее эта эпюра позволила определить сечение, в котором будет экстремум на эпюре .

Использование формулы (3.8) в виде:

(3.8)

не дает ответа на вопрос о месте нахождения экстремума и делает правильное построение эпюры более сложной задачей, требующей определенных навыков.

Пример 19. Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.38,а).

Степень статической неопределимости рамы:

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.38,б), т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.38,в).

Заменяя реакцию лишней связи соответствующей единичной силой,

(рис. 38,г) строим эпюру моментов (рис.38,д).

Грузовая эпюра моментов (рис.38,ж), построенная от одновременного действия всех внешних нагрузок (рис.38,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра ) и от совместного действия F и M (эпюра ). Эти варианты нагружения и эпюры представлены на рис.38,з и рис.39,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

Вычислим коэффициенты канонического уравнения:

Реакция лишних связи:

Эпюры N_z, Q_y, M_x для заданной системы, загруженной нагрузками F, M, q и X₁ (рис.39,г) представлены на рис.39,д,е,ж.

Как уже говорилось в гл.1, при построении эпюр и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В обоих рассмотренных примерах универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как балка (пример 18) и рама (пример 19) имеют степень статической неопределимости , а, значит, суммарная единичная эпюра (если ее построить) совпадет с единичной эпюрой . В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов .

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.38,а). Должно выполняться условие:

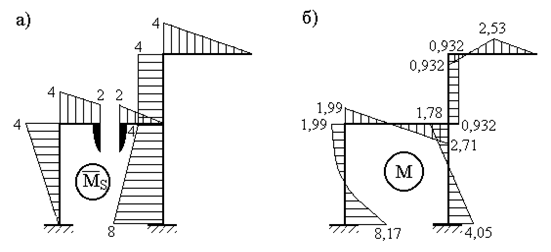
Покажем отдельно фрагменты перемножаемых эпюр (рис.38,д и рис.39,ж) для ригеля (рис.40,а,б) и стойки (рис.40,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.40,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры с осью (рис.40,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент определяется в виде:

Пересечение с осью означает, что в этом сечении 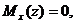поэтому подставляя числовые значения, для определения z при получим квадратное уравнение:

откуда (второй корень этого уравнения лишен физического смысла).

следовательно, расчет выполнен правильно.

Перейдем к рассмотрению более сложной системы – рамы с двумя лишними связями, для которой алгоритм расчета, приведенный в параграфе 3.3, можно реализовать в полном объеме.

Пример 20. Для рамы (рис.41,а) построить эпюры Выполнить промежуточные и окончательные проверки в соответствии с алгоритмом расчета, указанным в параграфе 3.3.

Заданная рама имеет в опорных закреплениях пять связей: две в опоре 1 и три в опоре 2, следовательно, система дважды статически неопределима:

Основную систему целесообразно выбрать путем удаления шарнирной опоры (рис.41,б). Соответствующая эквивалентная система изображена на рис.41,в.

Система канонических уравнений:

Для вычисления коэффициентов и свободных членов канонических уравнений строим единичные рис.41,г,д) и грузовую ( , рис.41, ж,з) эпюры изгибающих моментов, а для выполнения проверок – суммарную единичную эпюру (рис.41,е).

Коэффициенты системы канонических уравнений вычисляем путем перемножения соответствующих эпюр по правилу Верещагина. При этом обязательно учитываем разную жесткость элементов рамы (E2I – на левой стойке ригеля; EI – на правой стойке).

Для проверки вычисленных коэффициентов при неизвестных и свободных членов канонических уравнений используем суммарную единичную эпюру (рис. 41,е).

Должны выполняться два условия:

Вычисляем величины и .

таким образом, коэффициенты при неизвестных и свободные члены канонических уравнений вычислены правильно.

Вычисляем реакции лишних связей:

Строим эпюры продольных (N_z) и поперечных (Q_y) сил и изгибающих моментов (М_х) для заданной системы с учетом вычисленных реакций лишних связей (рис.43,а-г).

Для выполнения статической проверки необходимо вырезать жесткие узлы рамы 3 и 4 (рис.43,а) и убедиться в справедливости условий равновесия для каждого из них.

Условия равновесия для узла 3 (рис.42,а):

Условия равновесия для узла 4 (рис.42,б):

Таким образом, статическая проверка выполняется.

Для выполнения кинематической проверки перемножим суммарную единичную эпюру (рис.41,е) и окончательную эпюру изгибающих моментов М_х (рис.43,г):

следовательно, все проверки метода сил выполняются, и расчет проделан правильно.

Теперь рассмотрим примеры, иллюстрирующие различные способы использования симметрии.

Пример 21. Построить эпюры N_z, Q_y и M_x для симметричной рамы, загруженной несимметричной внешней нагрузкой (рис.44,а).

Заданная рама имеет два замкнутых бесшарнирных контура, следовательно, ее степень статической неопределимости

Записанная формально, без использования симметрии, система канонических уравнений метода сил имеет вид

Из многих возможных вариантов выбора основной системы наиболее целесообразным, максимально упрощающим расчет, является вариант, представленный на рис.44,б, полученный путем разрезания каждого из ригелей посредине пролета. Так как разрез стержня приводит к появлению трех неизвестных факторов (двух сил и момента), то эквивалентная система (рис.44,в) будет состоять из двух жестко защемленных рам, одна из которых загружена только неизвестными реакциями, а другая – такими же (по величине) реакциями и внешней нагрузкой.

Указанный выбор основной системы позволяет не только получить простые единичные эпюры (рис.44,г-и), но, что особенно важно, при этом целый ряд побочных коэффициентов системы канонических уравнений обращается в ноль. Это те коэффициенты, которые получаются путем перемножения симметричной и кососимметричной эпюр:

В силу теоремы о взаимности перемещений число нулевых коэффициентов удваивается. В результате формально записанная система канонических уравнений распадается на две самостоятельных системы:

II)

Вычисление коэффициентов этих систем уравнений (с обязательным учетом соотношения жестокостей элементов) приводит к следующим результатам:

Для выполнения проверки вычисленных перемещений строим суммарную единичную эпюру от одновременного действия шести единичных факторов (рис.45,б).

Вычисляем коэффициенты и :

следовательно, коэффициенты и свободные члены систем канонических уравнений вычислены правильно.

Подставляя вычисленные значения перемещений, получим системы канонических уравнений I и II в виде:

II.

Решение системы I и II дает значения реакций лишних связей:

Окончательные эпюры N_z, Q_y, M_x, построенные от одновременного действия вычисленных реакций и внешней нагрузки q (рис.45,в) показаны на рис.45,г,д,е.

Пример 22. Построить эпюры N_z, Q_y, M_x в симметричной раме (рис.46.а).

Рама имеет два замкнутых бесшарнирных контура, поэтому она шесть раз статически неопределима. При обычном подходе в этом случае было бы необходимо решить систему шести линейных уравнений, т.е. расчет был бы весьма трудоемким. Использование симметрии, как это будет показано ниже, позволит свести задачу к решению только лишь двух линейных уравнений.

Выберем основную систему, разрезая каждый из ригелей посредине пролета (рис.46,б). Но, в отличие от предыдущего примера, сформируем две эквивалентных системы, одну из которых загрузим симметричными составляющими внешней нагрузки (рис.46,в), а другую – обратно симметричными составляющими (рис.46,г). Легко убедиться в том, что сумма внешних нагрузок, приложенных к обеим эквивалентным системам, равна внешней нагрузке, приложенной к заданной раме.

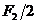
При действии симметричных самоуравновешенных сил и (рис.46,в), приложенных в узлах, в элементах рамы отсутствуют изгибающие моменты и поперечные силы, а продольные силы возникают только в ригелях и вычисляются непосредственно из условий равновесия узлов 3 и 5, или, что то же самое, 4 и 6:

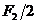
При действии обратносимметричных сил и (рис.46,г) в разрезах, сделанных по оси симметрии рамы, возникают обратносимметричные неизвестные поперечные силы Х₁, Х₂, а продольные силы и изгибающие моменты обращаются в ноль как симметричные усилия при обратносимметричной нагрузке.

Таким образом, для расчета рамы нужно составить только два канонических уравнения метода сил:

Единичные и грузовая эпюра изгибающих моментов показаны на рис.46,д,е,ж. Вычислим коэффициенты канонических уравнений путем перемножения соответствующих эпюр по правилу Верещагина:

Единичные и грузовая эпюра изгибающих моментов показаны на рис.46,д,е,ж.

Вычислим коэффициенты канонических уравнений путем перемножения соответствующих эпюр по правилу Верещагина:

Для проверки вычисленных перемещений используем суммарную единичную эпюру изгибающих моментов (рис.46,з).

После подстановки найденных значений коэффициентов при неизвестных и свободных членов в канонические уравнения и умножения последних на EI получим:

Таким образом, в результате раскрытия статической неопределимости исходная, шесть раз статически неопределимая система приведена к статически определимой системе (рис.46,и), загруженной внешней нагрузкой F₁ и F₂, продольными усилиями N₃₄ и N₅₆, а также вычисленными реакциями X₁ и X₂.

Эпюры продольных, поперечных сил и изгибающих моментов для заданной рамы показаны на рис.46,к,л,м.

Для выполнения универсальной кинематической проверки эпюры М_х используем суммарную единичную эпюру :

следовательно, задача решена правильно.

Пример 23. Построить эпюру изгибающих моментов для статически неопределимой рамы (рис.47,а), используя способ введения жестких консолей.

Этот способ используется для ортогонализации эпюр (т.е. для получения нулевых перемещений – коэффициентов канонических уравнений) в пределах каждого замкнутого или открытого с защемленными концами симметричного контура. Для ортогонализации эпюр с помощью жестких консолей соответствующие неизвестных переносятся в некоторую точку, называемую упругим центром. Положение этой точки определяется как положение центра тяжести условного тонкостенного сечения с толщиной

Заданная рама имеет степень статической неопределенности:

Для выбора основной системы (рис.47,б) используем то обстоятельство, что левый (П-образный) контур рамы симметричен. Разрежем его по оси симметрии, что будет эквивалентно удалению трех связей и появлению трех неизвестных реакций. Четвертую связь устраним путем удаления шарнирно-подвижной опоры. Введение в месте разреза жестких консолей с приложенными на их концах реакциями Х₁, Х₂, Х₃ совместно с реакцией Х₄ и внешними нагрузками приводит к эквивалентной системе (рис.47,в).

Определим положение упругого центра, т.е. фактически длину жестких консолей (рис.47,г), вычисляя координаты центра тяжести условного тонкостенного П-образного сечения:

Х_с=0;

Единичные эпюры изгибающих моментов показаны на рис.47,д,е,ж,з, а эпюра моментов от внешних нагрузок – на рис.47,и.

Учитывая, что результат перемножения симметричной эпюры на кососимметричную равен нулю, систему канонических уравнений метода сил рассматриваемой рамы запишем в виде:

Вычислим коэффициенты уравнений, используя, как обычно, способ Верещагина:

Для проверки правильности вычисления коэффициентов и свободных членов канонических уравнений построим суммарную единичную эпюру изгибающих моментов (рис.48,а) и определим коэффициенты и .

Следовательно, коэффициенты и свободные члены канонических уравнений вычислены правильно. Решение системы канонических уравнений дает следующие значения неизвестных:

Окончательная эпюра моментов для заданной рамы показана на рис.48,б.

Читатель имеет возможность самостоятельно убедиться в правильности построенной эпюры, перемножив ее с суммарной единичной эпюрой (результат, как известно, должен равняться нулю).

Глава 4

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Источник