11 Умножение двоичных чисел
11.1 Методы умножения бинарных чисел
Рассмотрим основные способы выполнения операции умножения для различных систем cчисления. Самым распространенным способом умножения чисел является способ поразрядного умножения множимого на множитель, начиная с младшего разряда — 1-й способ, начиная со старшего разряда – 2-способ.
Анализ способов умножения чисел в десятичной системе счисления показывает, что операция умножения состоит из поразрядного умножения множимого на множитель с переносом переполнения в старший разряд, сдвига частных произведений на один разряд влево (вправо), суммирование частных произведений.
В двоичном счислении эта задача значительно упрощается, т.к. умножать поразрядно нет необходимости. В самом деле, если умножать множимое на «1», то это повторение множимого со сдвигом на один разряд вправо (влево), а на «0» — записываются одни нули со сдвигом.
В обоих случаях операция умножения состоит из ряда последовательных операций сдвига и сложения частных произведений. Таким образом, операция умножения сводится к сложению частных произведений, которые получаются из множимого с соответствующим сдвигом или нулей, если в разряде множителя «нуль», или множимого, если в разряде множителя 1. Рассмотрим, как производит умножение компьютер.
11.2 Умножение чисел с фиксированной запятой на дспк
Запишем машинное изображение множимого и множителя в форме с фиксированной запятой в прямом коде. Anp=SgA,α1α2. αn; Bпр=SgB,b1b2. bn. Тогда, их произведение запишется как Cnp=Sgc,с1с2. сn, где Sgc= SgASgB, где — знак сложения по mod2. (1)
Таким образом, при использовании ДСПК, знак произведения определяется отдельно от цифровой части, затем выполняется операция умножения. Она выполняется в соответствии с заданной структурой множительного устройства (см. например, рисунок 11.1).
Рисунок 11.1-Структурная схема устройства умножения
По методу 2 умножение начинается с младшего разряда и сдвигается вправо сумма частных произведений.
Пример. Умножить числа Апр = 1,11010 = — 26; Впр, = 0,11001 = 25, С= -650.
Решение: Определяется знак произведения 1 0 =1
Зададим: 1) сумматор имеет 10 разрядов (без знака).
2) регистры имеют по 5 разрядов (без знака).
Последовательность действий представим таблицей 11.1.
Для упрощения записи таблиц, принимаем следующие условные обозначения:
-оператор := присваивания значения (блоку слева присваивается значение, указанное справа от операнда);
-оператор 
-обозначения, например, [См] — содержимое сумматора;
-обозначение И. П. — исходное положение;
-обозначения Апр., Впр. — цифровая часть множимого и множителя в прямом коде.
Если при умножении возникает единица переноса из старшего разряда, то ее сохраняют путем сдвига т.е. необходимо предусматривать в цифровом автомате стробирование сигнала переполнения для выработки сдвига на один разряд.
Этот способ умножения получил наибольшее распространение в практике цифровых автоматов.
11.3 Умножение чисел с плавающей запятой
Так как числа с плавающей запятой представляются мантиссой и порядком, то выполнение операции умножения состоит из двух действий:
Результат умножения может получиться денормализованным, поэтому требуется проверка на нормализацию числа и, при необходимости, его нормализация с соответствующей коррекцией порядка результата. Устройство умножения чисел с плавающей запятой представлено автоматом со структурой рисунка 11.2.
Пример. А= – 0,11001*2 –-3 ; В=0,10011*2 1
Сложение порядков производим в обратном коде, См. — 10 разрядов, Рг. — 5 разрядов. Умножение мантисс приведено в таблице 11.2. Определим значение порядка
Так как мантисса результата не удовлетворяет нормализации слева, т.е. δ=1,γ=0, то производится сдвиг мантиссы влево на один разряд mC = 1,1110110110 и коррекция порядка
В машинном виде будет соответствовать коду 11.1110110110.11.11, при условии выделения для порядка всего двух разрядов.
Примечание. Точки, разделяющие знак мантиссы, мантиссу, знак порядка, порядок в машинном коде не проставляются.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Умножение двоичных чисел машинным методом.
Умножение двоичных чисел машинным методом производится по следующим алгоритму:
1. Определяют знак произведения путём сложения по модулю два знаковых разрядов множителей.
2. Перемножение модулей чисел начиная с младшего разряда множителя одним из следующих способов умножения: 1)Множимое неподвижно сумматор частичных произведений сдвигается вправо. 2)Сумматор частичных произведений неподвижен множимое сдвигается влево.
Оба способа дают одинаковый результат, в обоих случаях умножение начинается с анализа младшего разряда множителя. Умножение производится в прямом коде.
1) Способ анализируется очередной разряд множителя: Если он равен 1 то к содержимому сумматора прибавляется множимое и сумматор сдвигается вправо. Если он равен 0 то производится только сдвиг сумматора вправо. Причём количество сдвигов равно количеству разрядов множителя, а количество прибавлений множимого к сумматору равно количеству единиц во множителе.
2) Анализируется второй разряд множителя если он равен единицы то множимое прибавляется в сумме частичных произведений и множимое сдвигается в лево на один разряд. Если он равен 0 то производится только сдвиг множимого влево.
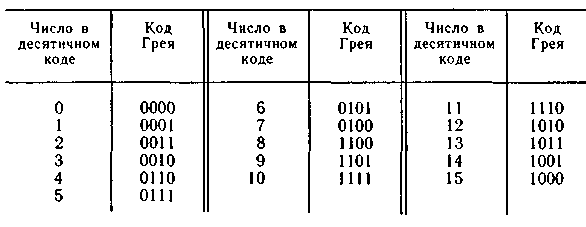
Особенно важным среди циклических является код Грэя. Он строится на базе двоичного по следующему правилу: старший разряд остаётся без изменения; каждый последующий разряд инвертируется если предыдущий разряд исходного двоичного кода равен единице.
При использовании кода 4221 каждая цифра записывается в виде 4-х разрядной группы. Но её разряды начиная с левого представляют величины 4221. (д.з. сделать таблицу с кодом Грея от 0 до 15 и таблицу с кодами с остатком 3 и 4221 от 0 до 9).
Коды с выявлением ошибок
Общие сведения о кодах с выявлением ошибок
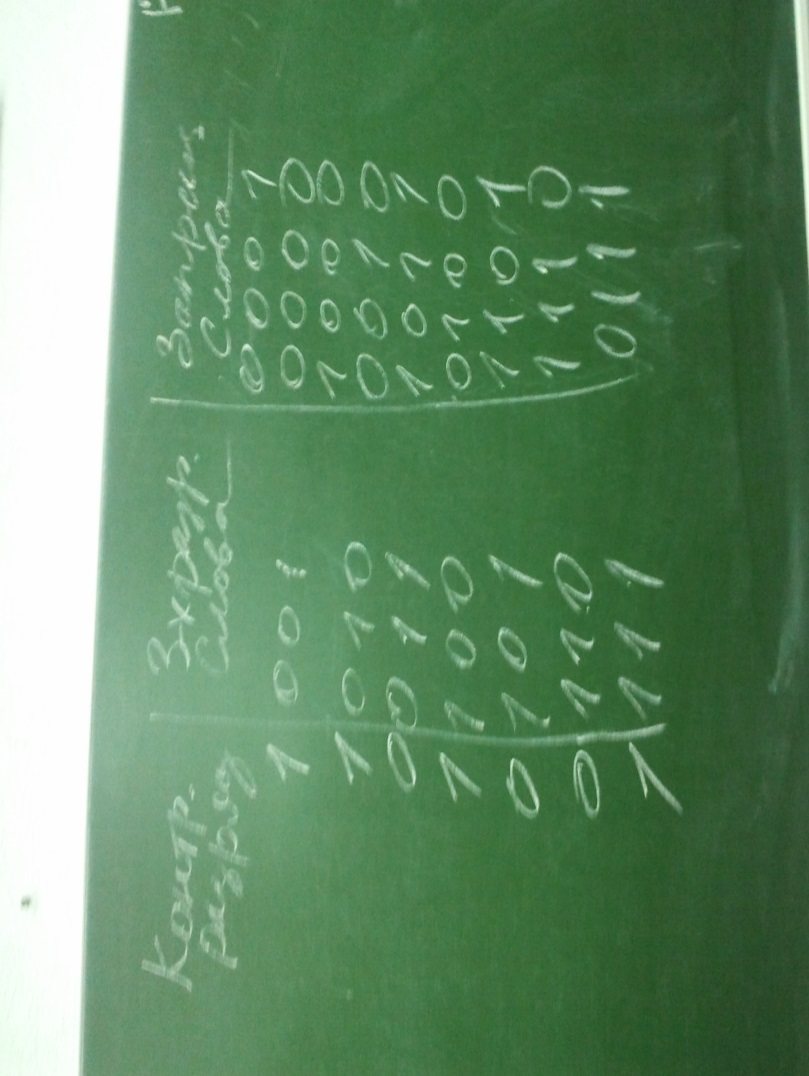
Одним из важнейших аспектов организации хранения и передачи кодов данных является обеспечение их надёжности и без ошибочности применяя специальные методы кодирования можно обеспечить контроль за появлением ошибки и даже восстановление исходного кода после её обнаружения. Применение этих методов позволяет снизить вероятность появления ошибки до 10 -9 и ниже. Общим методом обеспечения надёжности хранения и передачи данных в компьютере и по линиям связи является включение в код дополнительных контрольных разрядов. Существует много различных вариантов этого метода, рассмотрим код с проверкой чётности. При формировании кода слова в контрольный (дополнительный разряд) записывается 0 или 1 таким образом, что бы сумма единиц в слове, включая контрольный разряд, была чётной.
Пример (контроль по чётности 3-х разрядных слов):
В дальнейшем при всех передачах, слово передаётся вместе со своим контрольным разрядом. Если при передаче информации приёмное устройство обнаруживает, что в принятом слове значение контрольного разряда не соответствует чётности суммы единиц слова, то это воспринимается как признак ошибки. Код контроля по чётности обнаруживает все одиночные ошибки и все случаи не чётного числа ошибок. При одновременном возникновении двух или любого чётного числа ошибок, код с проверкой чётности не обнаруживает ошибок.
Существуют более развитые способы кодирования, которые не только позволяют установить факт появления ошибок большой кратности, но и обеспечивают их исправление. К таким способам относятся коды, принцип построения которых предложил Р. Хемминг.
Рассмотрим общую идею построения кодов Хемминга на следующем примере:
Пусть имеется исходный, 4-х битный код:
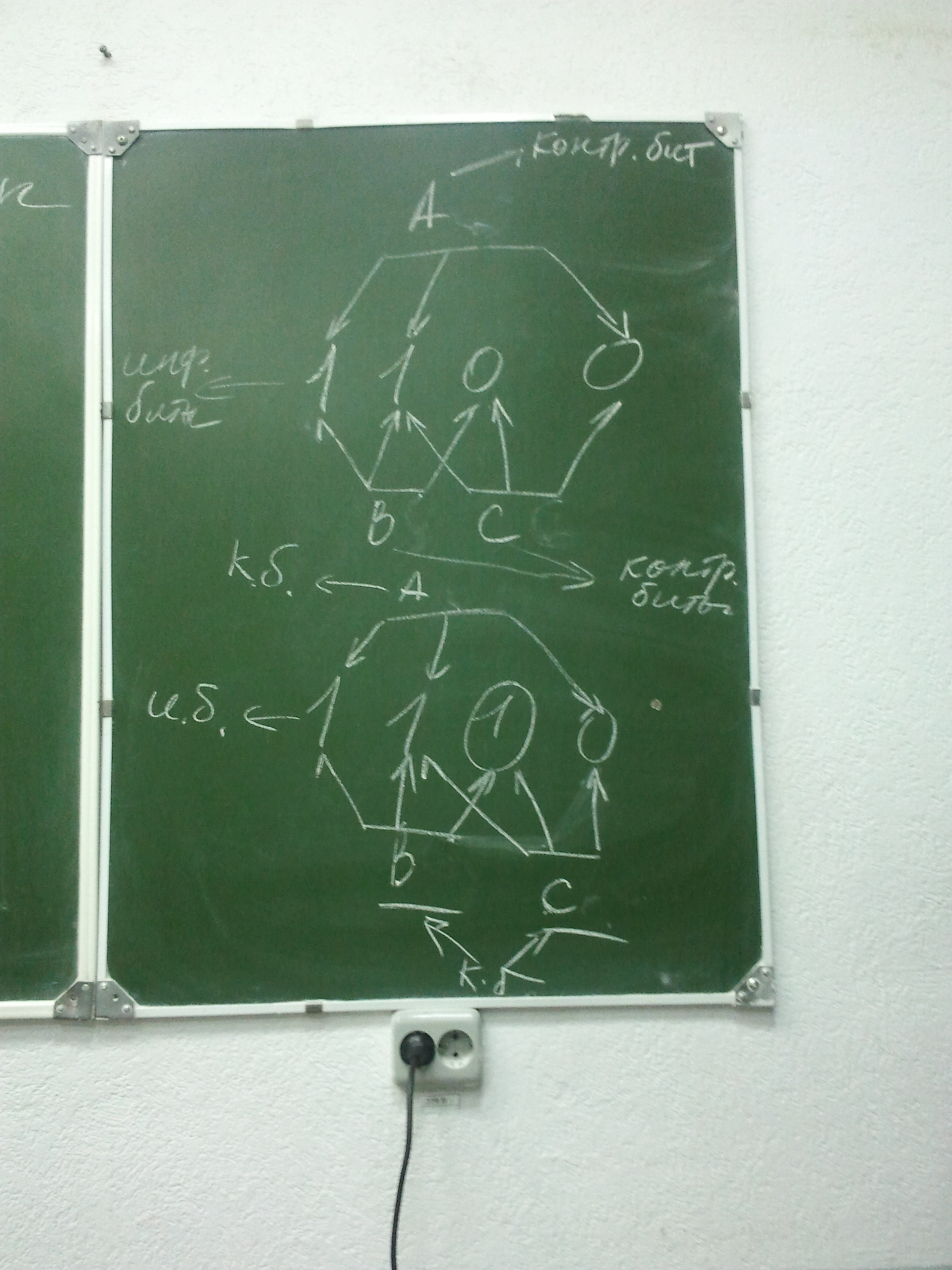
Чтобы не только обнаружить, но и исправить вероятную одиночную ошибку , предлагается каждую тройку битов снабдить одним контрольным разрядом (можно ограничится тремя тройками) количество единиц в каждой группе (тройка битов вместе с контрольным разрядом) должно быть не чётным. На рисунке изображены: исходный код и значения контрольных битов A B C. В каждой выбранной тройке.
Если во время выполнения действий один из битов окажется искажённым, то во всех группах в которые входит ошибочный бит, контроль не чётности покажет наличие ошибки. Следовательно, для определения положения ошибочного вида в коде достаточно выбрать разряд входящий во все группы в которых нарушена не чётность (на рисунке эти биты подчёркнуты). Ошибочный бит должен принадлежать одновременно двум группам. После обнаружения сбойного бита исправление кода осуществляется его инвертирование.
Алгебра логики и теоретические основы синтеза цифровых устройств
Тема 2.1: Элементы математической логики
Понятие алгебры-логики. Основные логические операции и логические элементы
Для математического описания работы вычислительных устройств, синтеза и анализа схем (синтез – процесс создания устройства; анализ – упрощение устройства) используется алгебра логики (Белева алгебра). Область алгебры-логики состоит из множества высказываний обозначается A B C…X,Y.
Высказывание – законченное предложение, которое может иметь два значения истинности: либо быть истинным (А – истинно: А=1) либо быть ложным (С – ложно: С=0).
Высказывания могут быть истинными или ложными: первое не зависит от высказываний, а второе образуется из двух и более простых высказываний. Простое высказывание называют логическим переменным, а сложное логической функцией этих переменных переключательный функции (ПФ)
Операции алгебр логики:
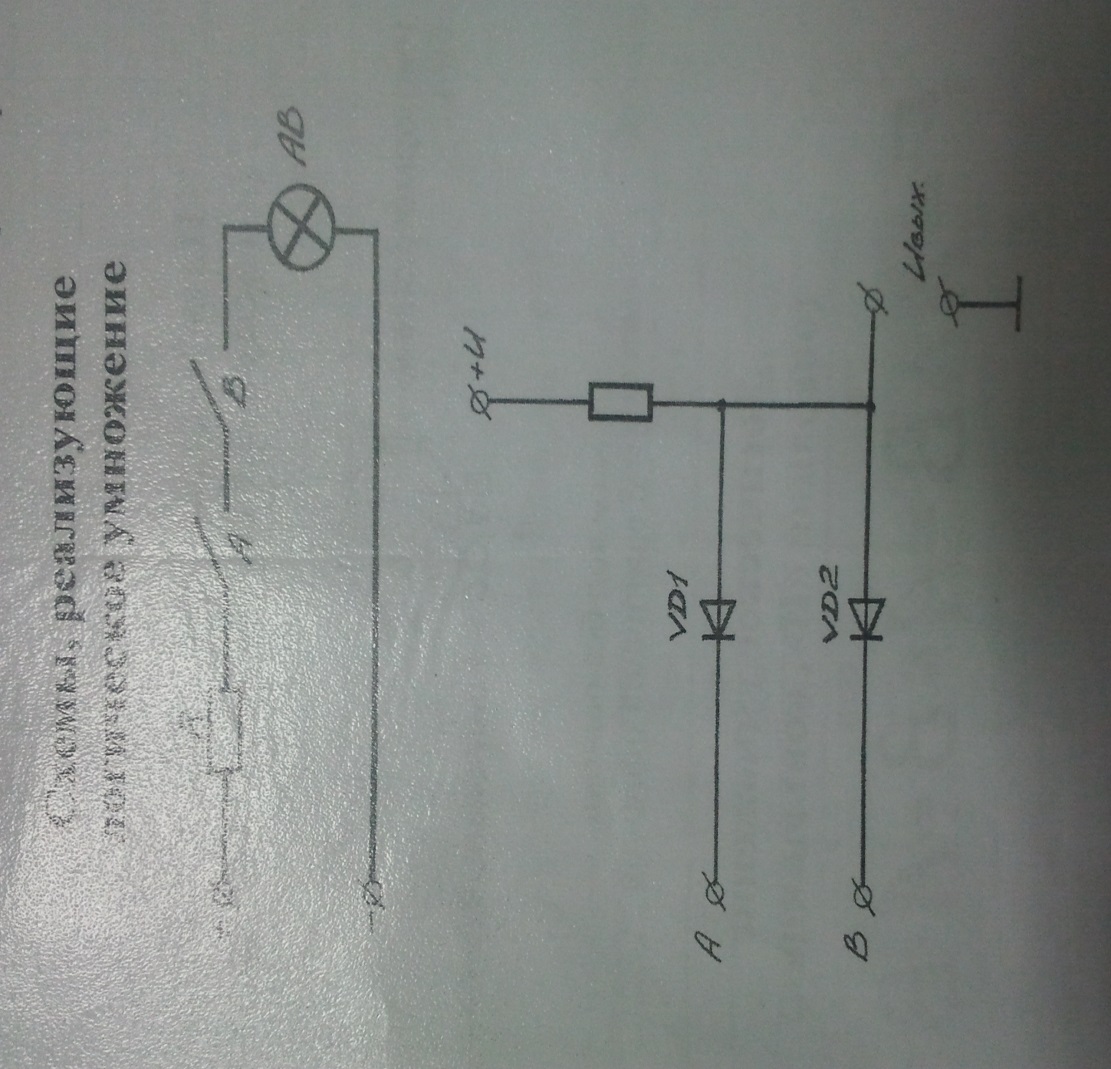
1. Логическое умножение (операция «И», конъюнкция)
Схема реализующая эту логическую операцию, называется схемой «И»
На выходе схемы «И» сигнал соответствует логической единице, тогда и только тогда, когда на всех входах одновременно будет сигнал логической единицы. Разрешающим уровнем схемы и является уровень логической единицы схемы «И», логическая функция от «н» переменной будет иметь 2 n строк.
Схемы, реализующие логическое умножение:
На выходе схемы «ИЛИ» всегда соответствует логическому нулю, тогда и только тогда, когда на всех входах одновременно будет сигнал логического нуля. Разрешающим для схемы «ИЛИ» является уровень логического нуля.
Сложение по модулю 2
(Операция «исключающее ИЛИ», неравнозначность)
| А | В | А+В | -А+В |
Основные законы логики
Тема 2.2: Формы логических функций и их использование для синтеза логических схем.
Формы логических функций:
F=A—C BvAC 1BvAC BA= ABCvA-BCvAB-C= ACvAB= —ACvAB= -AC*-AB
ПФ – могут быть выражены различными логическими формулами, благодаря возможности проведения над ними эквивалентных преобразований. На практике наиболее удобными для представления ПФ оказываются дизъюнктивные и конъюнктивные формы.
Эти формы представляют собой дизъюнкции элементарных конъюнкций или конъюнкций элементарных дизъюнкций.
Конъюнкция(дизъюнкция) любого числа называется элементарной если со множетялями(слагаемыми) в ней являются одиночные аргументы, либо описание одиночных аргументов.
Дизъюнктивной, нормальной формой(ДНФ), ПФ называется дизъюнкция любого числа элементарных конъюнкций, например:
Ранг элементарной конъюнкции(дизъюнкции) определяется числом переменных входящих в эту конъюнкцию(дизъюнкцию).
Совершенной ДНФ(СДНФ) ПФ имеющее n аргументов называется такая форма в которой все конъюнкции имеют ранг n:
ПФ может быть задана словестно, в виде таблицы истинности логического выражения. По словестному описанию составляют таблицу истинности, а затем записывают СДНФ в ПФ.
СДНФ, ПФ записывается по таблице истинности в следующей Последовательности:
1. Из таблицы истинности выделяются строки, в которых функция принимает значение единицы.
2. Записываются составляющие формулы в виде конъюнкции переменных или их отрицания. Если переменная в данном наборе = 1, то она входит в формулу как не отрицательная.
3. Конъюнкции определяют знаком дизъюнкции.
Записать ПФ устройство функционирующего по следующему правилу: Сигнал на выходе схемы = 1, если хотя бы на двух входах из трёх отсутствует уровень логической единицы.
Конъюнктивные формы представления ПФ используются реже, чем дизъюнктивные. Конъюнктивной, нормально формой(ПНФ) ПФ называется конъюнкция элементарных дизъюнкций:
Все дизъюнкции имеют ранг ПФ:
Тема 2.3. Логические элементы и схемы. Классификация
Функционально полные системы логических функций
Функционально полной системой или базисом переключательных функций F1,F2,…,Fn с помощью которой может быть представлена любая функция алгебры логики. Функционально полными системами называются базисы:
1. Базис: И, ИЛИ, НЕ
4. Базис (или базис Шеффера): И-НЕ
5. Базис (или базис Пирса): ИЛИ-НЕ
Базис И, ИЛИ, НЕ принято называть основным т.к. любая сложная ПФ может быть записана в виде СДНФ или СКНФ.
Базисы могут быть избыточными и минимальными:
1. Базис является избыточной, т.к. возможно исключение из него некоторых функций, например: используя законы двойного отрицания и Де-Моргана можно исключить, либо функцию И, заменяя её на ИЛИ, НЕ(Базис 3); либо ИЛИ, заменяя её на И, НЕ(Базис 2). Базисы 2, 3 называют нормальными( минимальными), т.к. при удалении из этих базисов хотя бы одной функции функционально полная система превращается в не полную.
Абстрактный автомат имеет один входной и один выходной каналы.
Под законом функционирования понимается совокупность правил описывающих последовательность переключения состояния Автомата и последовательность выходных сигналов в зависимости от последовательности входных сигналов .
В зависимости от способа определения значений выходных сигналов различают 2 типа автоматов:
1) Автоматы Мура описываются системой уравнений a(t+1)=q(a(t),z(t)); w(t)=Л(a(t))
В автоматах мура выходной символ не зависит явно от входного символа z(t) а переделяется внутренним состоянием Автомата
2) Автоматы Мили описываются системой уравнений a(t+1)=q(a(t),z(t)); w(t)=Л(a(t),z(t))
В автомате Мили выходной сигнал в момент времени t зависит как от внутреннего состояния автомата в момент t так и от входного сигнала в момент t.
Источник