Способ укрупнения интервалов это

Метод укрупнения интервалов.

Поможем написать любую работу на аналогичную тему

Если рассматривать уровни экономических и социальных показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в различных направлениях, в рядах динамики наблюдается их снижение и/или повышение. Из-за этого трудно заметить основную тенденцию развития явления. Одним из наиболее простых приемов обнаружения общей тенденции развития явления является метод укрупнения интервалов ряда динамики. Смысл приема заключается в том, что первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени, например, ряд, содержащий данные о месячном выпуске продукции, может быть преобразован в ряд квартальных данных. Вновь образованный ряд может содержать либо абсолютные величины за укрупненные по продолжительности промежутки времени (эти величины получают путем простого суммирования уровней первоначального ряда абсолютных величин), либо средние величины. При суммировании уровней или выделении средних по укрупненным интервалам отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживаются действие основных факторов изменения уровней (общая тенденция)

Пример. В табл. 12. приведены сведения о выпуске продукции машиностроительным предприятием за последние десять лет.

Выпуск продукции за последние 10 лет (млн. грн.)

Источник

Важнейшие приемы анализа рядов динамики: укрупнение интервалов, метод скользящей средней, аналитического выравнивания.

Поможем написать любую работу на аналогичную тему

В ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления (тренда) и сглаживание случайных колебаний. Для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания.

Выделяют три основных способа обработки динамического ряда:

а) укрупнение интервалов динамического ряда и расчет средних для каждого укрупненного интервала;

б) метод скользящей средней;

в) аналитическое выравнивание (выравнивание по аналитическим формулам).

Укрупнение интервалов — наиболее простой способ. Он заключается в преобразовании первоначальных рядов динамики в более крупные по продолжительности временных периодов, что позволяет более четко выявить действие основной тенденции (основных факторов) изменения уровней.

По интервальным рядам итоги исчисляются путем простого суммирования уровней первоначальных рядов. Для других случаев расcчитывают средние величины укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.

Скользящая средняя — это такая динамическая средняя, которая последовательно рассчитывается при передвижении на один интервал при заданной продолжительности периода. Если, предположим, продолжительность периода равна 3, то скользящие средние рассчитываются следующим образом:

При четных периодах скользящей средней можно центрировать данные, т.е. определять среднюю из найденных средних. К примеру, если скользящая исчисляется с продолжительностью периода, равной 2, то центрированные средние можно определить так:

Первую рассчитанную центрированную относят ко второму периоду, вторую — к третьему, третью — к четвертому и т.д. По сравнению с фактическим сглаженный ряд становится короче на (m — 1)/2, где m — число уровней интервала.

Важнейшим способом количественного выражения общей тенденции изменения уровней динамического ряда является аналитическое выравнивание ряда динамики, которое позволяет получить описание плавной линии развития ряда. При этом эмпирические уровни заменяются уровнями, которые рассчитываются на основе определенной кривой, где уравнение рассматривается как функция времени. Вид уравнения зависит от конкретного характера динамики развития. Его можно определить как теоретически, так и практически. Теоретический анализ основывается на рассчитанных показателях динамики. Практический анализ — на исследовании линейной диаграммы.

Задачей аналитического выравнивания является определение не только общей тенденции развития явления, но и некоторых недостающих значений как внутри периода, так и за его пределами. Способ определения неизвестных значений внутри динамического ряда называют интерполяцией. Эти неизвестные значения можно определить:

1) используя полусумму уровней, расположенных рядом с интерполируемыми;

2) по среднему абсолютному приросту;

3) по темпу роста.

Способ определения количественных значений за пределами ряда называют экстраполяцией. Экстраполирование используется для прогнозирования тех факторов, которые не только в прошлом и настоящем обусловливают развитие явления, но и могут оказать влияние на его развитие в будущем.

Экстраполировать можно по средней арифметической, по среднему абсолютному приросту, по среднему темпу роста.

При аналитическом выравнивании может иметь место автокорреляция, под которой понимается зависимость между соседними членами динамического ряда. Автокорреляцию можно установить с помощью перемещения уровня на одну дату. Коэффициент автокорреляции вычисляется по формуле

Автокорреляцию в рядах можно устранить, коррелируя не сами уровни, а так называемые остаточные величины (разность эмпирических и теоретических уровней). В этом случае корреляцию между остаточными величинами можно определить по формуле

Анализ рядов динамики предполагает и исследование сезонной неравномерности (сезонных колебаний), под которыми понимают устойчивые внутригодовые колебания, причиной которых являются многочисленные факторы, в том числе и природно-климатические. Сезонные колебания измеряются с помощью индексов сезонности, которые рассчитываются двумя способами в зависимости от характера динамического развития.

При относительно неизменном годовом уровне явления индекс сезонности можно рассчитать как процентное отношение средней величины из фактических уровней одноименных месяцев к общему среднему уровню за исследуемый период:

В условиях изменчивости годового уровня индекс сезонности определяется как процентное отношение средней величины из фактических уровней одноименных месяцев к средней величине из выровненных уровней одноименных месяцев:

Источник

Метод укрупнения интервалов

Таблица 6.2 Число

месяца Реализация продукции, ден.ед. Скользящая средняя трехдневная пятидневная семидневная 5 7 — — — 6 6 6,67 — — 7 7 7,00 7,6 — 8 8 8,33 8,0 7,86 9 10 9,00 6,4 7,86 10 9 9,00 8,4 8,57 13 8 8,00 9,0 9,57 14 7 8,67 9,8 11,00 15 11 10,67 11,6 11,14 16 14 14,33 12,2 11,00 17 18 14,33 12,4 11,14 18 11 12,33 12,0 12,57 21 8 9,33 12,6 12,71 22 9 11,33 11,4 13,43 23 17 12,67 13,0 12,28 24 12 16,00 13,4 13,86 25 19 13,67 16,0 14,86 26 10 17,00 15,6 16,14 29 22 16,33 16,8 — 30 15 18,33 — — 31 18 — — — Пусть в табл. 6.2 приведены данные о реализации продукции магазином. Вычислим трех-, пяти- и семидневные скользящие средние. Результаты вычислений приведены в той же таблице.

Из анализа результатов третьего, четвертого и пятого столбцов следует, что с увеличением интервала сглаживания тенденция динамического ряда прослеживается более ярко. Этот факт можно наглядно подтвердить, изобразив уровни динамического ряда и скользящие средние на графиках (рис. 3.2, а — г). С укрупнением интервалов степень сглаживания динамических рядов увеличивается и четко прослеживается тенденция.

При графическом анализе динамических рядов используется ломаная кривая, которая строится в прямоугольной системе координат. Для построения ломаной линии в системе координат хОу по оси Ох откладывается в определенном масштабе время t, а по оси Оу в соответствующем масштабе — уровни динамического ряда уг Масштабы для этих двух осей выбираются так, чтобы график не был слишком плоским и динамичным. Каждая точка на плоскости хОу показывает уровень ряда, отнесенный к определенному периоду или моменту.

Рис.6.1 6.5. Г рафический метод

Пусть товарооборот крупного универсального магазина характеризуется динамическим рядом, приведенным в табл. 6.3.

Таблица 6.3 Год t 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 Товарооборот yt, млн р. 500 600 650 900 800 1000 1200 1400 1600 1500 1700 Построим график товарооборота в прямоугольной системе координат. На оси Ох отложим годы t, а на оси Оу — товарооборот yt (рис. 6.2). Построенный график позволяет визуально или приближенно определять товарооборот за

отдельные годы рассматриваемого периода, абсолютные приросты товарооборота за любой субпериод всего рассматриваемого периода, сравнивать абсолютные приросты товарооборота за исследуемые годы.

График динамического ряда, построенный указанным путем, непригоден для визуальной или приближенной количественной оценки темпов роста, как цепных, так и базисных, так как он не дает представления о соотношении уровней за тот или иной период, о сравнительной величине этих соотношений за разные периоды времени. Поэтому строится полулогарифмический график, в котором на оси абсцисс в обычном масштабе откладывается время, а на оси ординат в логарифмическом масштабе — уровни ряда. В силу свойств логарифмов (логарифм произведения равен сумме логарифмов, логарифм отношения — разности логарифмов) ординаты точек ломаной кривой на полулогарифмическом графике пропорциональны темпам роста, аналогично тому, как на обычной шкале эти ординаты пропорциональны уровням ряда и абсолютным приростам. Указанное свойство логарифмической шкалы применяется для анализа темпов роста уровней динамического ряда.

m = V(lgymax — lgymin ), (6-31)

где l — принятая длина масштабной шкалы; ymax, ymin — соответственно наибольший и наименьший уровни динамического ряда.

Построение логарифмической шкалы начинают с нанесения опорных чи-

сел, значения которых находят по формуле

где l — длина отрезка, которая в принятом масштабе соответствует избранным опорным числам; m — масштаб; у — число (уровень динамического ряда), которое должно быть нанесено на шкалу.

После построения логарифмической шкалы уровней динамического ряда строят систему координат, на ось ординат которой наносят эту шкалу, а на ось абсцисс — время. Точки плоскости хОу с соответствующими координатами соединяют отрезками прямых и получают ломаную линию, которая характеризует изменение темпов роста экономического показателя.

Для того чтобы определить базисные темпы роста товарооборота, достаточно с помощью вспомогательных средств (циркуля, линейки) определить ординату интересующей нас точки и сравнить этот отрезок с процентной шкалой, построенной в логарифмическом масштабе, вверх или вниз от отметки 100 % в зависимости от того, больше или меньше 100 % этот темп роста. Отметим, что в каждом конкретном случае должна быть построена процентная логарифмическая шкала, масштаб которой соответствует масштабу логарифмической шкалы уровней динамического ряда. Например, если логарифмический масштаб шкалы уровней равен 100 мм, то и логарифмический масштаб процентной шкалы должен быть равен 100 мм. Тогда логарифмам в интервале (0; 1) соответствуют проценты в интервале (100 %; 1000 %).

На практике удобно пользоваться подвижной процентной шкалой, которая накладывается на график для измерения темпа роста. При этом отметка 100 % на этой подвижной шкале должна соответствовать отметке уровня, принятого за базу. Для вычисления цепных темпов роста определяют разность ординат сравниваемых уровней и по логарифмической процентной шкале находят интересующий темп роста.

Таким образом, построив ломаную линию, характеризующую изменение уровней или темпов роста динамического ряда, визуально можно оценить наличие тенденции изменения динамического ряда.

Источник

Ряды динамики в статистике

9.3. Методы анализа основной тенденции в рядах динамики

Комплексный анализ динамических рядов, как правило, включает не только расчет характеристик интенсивности изменения уровней ряда при переходе от одного момента или промежутка времени к другому (абсолютных приростов, коэффициентов и темпов роста и прироста), а также нахождение обобщенных средних характеристик (среднего уровня ряда, средних темпов роста и прироста), но и выявление основных закономерностей в развитии динамического ряда. Определение тенденции развития, построение модели, описывающей изменение явления во времени, прогнозирование явления — все это важнейшие задачи при изучении динамических рядов экономических и социальных показателей.

На формирование уровней динамического ряда влияет множество различных факторов, которые по характеру воздействия можно объединить в три группы:

1. действующие долговременно и определяющие основную тенденцию развития явления;
2. действующие периодически — сезонные и циклические колебания;
3. вызывающие случайные колебания уровней динамического ряда.

Соответственно, для анализа закономерности изменения уровней ряда динамики во времени применяют следующую модель:

где Т_t — основная тенденция ряда ( тренд );

S_t — циклические (в частности, сезонные) колебания;

е_t — случайные колебания.

В аддитивной модели ряд динамики представлен как сумма перечисленных компонент [y_t = T_t + S_t + e_t], в мультипликативной модели — как их произведение []. В дальнейшем будем исходить из предположения мультипликативной формы связи между компонентами ряда динамики.

Тенденцией развития, или трендом, называется сформировавшееся направление развития явления во времени под воздействием постоянно действующих факторов. Судить о наличии тенденции в динамическом ряду на основе его визуального анализа можно лишь тогда, когда четко видно, что при переходе от одного момента времени к другому уровни ряда возрастают или убывают. Однако, как правило, нельзя сразу сказать, есть или нет тенденция в изменении уровней динамического ряда. Для этого применяются специальные методы.

К методам выявления основной тенденции развития динамического ряда (Т_t) относятся:

• метод укрупнения интервалов;
• метод скользящей средней;
• аналитическое выравнивание динамических рядов.

Рассмотрим их подробнее.

9.3.1. Метод укрупнения интервалов

Применение метода укрупнения интервалов рассмотрим на основе данных табл. 9.13.

Таблица 9.13. Поставки товаров в торговую сеть

Месяц	Поставка товаров, млн руб.
Январь	80
Февраль	78
Март	75
Апрель	80
Май	82
Июнь	85
Июль	87
Август	82
Сентябрь	85
Октябрь	84
Ноябрь	86
Декабрь	88

Как видим, визуальный анализ данных не позволяет сделать какие-либо выводы о наличии тенденции в данном динамическом ряду: в отдельные месяцы, например, в феврале, марте, августе, октябре и декабре, поставки товаров снижались по сравнению с предыдущими месяцами, в остальные периоды — возрастали.

Применим к исходным данным метод укрупнения интервалов, образовав новый динамический ряд с более крупными временными периодами — кварталами, и рассчитаем средний месячный объем поставок в каждом квартале (табл. 9.14).

Таблица 9.14. Среднемесячные поставки товаров

Квартал	Среднемесячные поставки товаров, млн руб.
I	77.7
II	82.3
III	84.0
IV	84.7

Итак, по новым, более крупным интервалам уже четко видно, что значения исследуемого признака во временном аспекте имеют тенденцию к возрастанию.

Применение рассмотренного метода в основном ограничивается теми ситуациями, когда исходные данные относятся к дням, неделям или месяцам года, так как значения исследуемого признака по более мелким временным интервалам больше подвержены случайным колебаниям. Если временные промежутки представляют собой годы, то укрупнение интервалов становится малоэффективным.

9.3.2. Метод скользящей средней

Следующий способ выявления тенденции в динамическом ряду основан на расчете и анализе так называемых скользящих (подвижных) средних.

Скользящими (подвижными) средними называются средние арифметические значения показателя, исчисленные по новым m-членным укрупненным интервалам. Правила построения этих интервалов следующие. Первый из интервалов включает первые m уровней ряда динамики, второй интервал образуется путем исключения первого члена укрупненного интервала и замены его последующим элементом ряда динамики, имеющим номер (m + 1) и т.д. — до включения в интервал последнего уровня ряда. По вычисленным подобным путем подвижным средним делают вывод о существовании тенденции в динамическом ряду.

Если в качестве укрупненного интервала используют период в три месяца, то первая подвижная трехчленная средняя вычисляется как средняя арифметическая из данных за январь, февраль и март, вторая — как средняя арифметическая из данных за февраль, март, апрель и т.д. Значения подвижных средних относят к конкретному временному периоду, соответствующему середине укрупненного интервала.

Проведем сглаживание ряда методом скользящей средней по трем членам (табл. 9.15).

Таблица 9.15. Сглаживание ряда динамики методом скользящей средней по трем членам

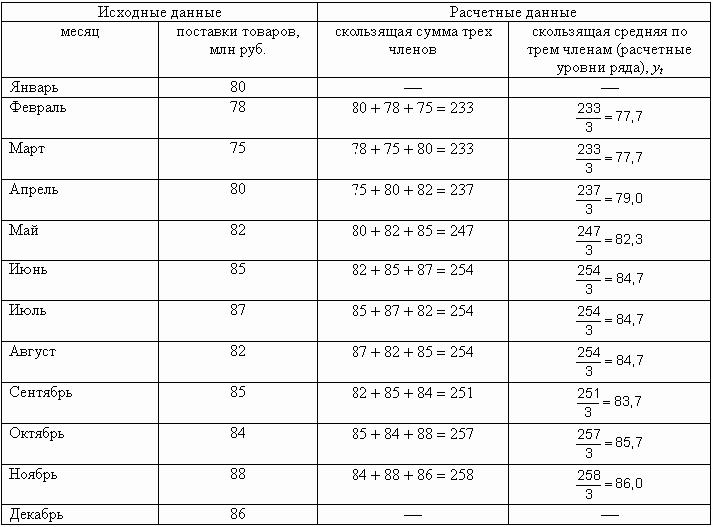В нашем примере первая скользящая средняя относится к февралю, вторая — к марту и т. д.

В тех случаях, когда сглаживание проводится по четному числу уровней ряда динамики, середина временного интервала сглаживания будет находиться между двумя моментами (периодами) времени. Например, если проводить сглаживание по четырем членам, середина первого интервала будет находиться между февралем и мартом, второго интервала — между мартом и апрелем и т.д. В таких случаях возникает необходимость центрирования полученных результатов для отнесения сглаженных значений показателя к конкретным периодам или моментам времени. Расчет центрированных скользящих средних может проводиться в два этапа:

1. определение скользящих сумм и нецентрированных скользящих средних по четному числу уровней ряда динамики;
2. исчисление центрированных скользящих средних из двух смежных ранее исчисленных нецентрированных скользящих средних и отнесение их к соответствующим периодам или моментам времени.

Методика расчета центрированных скользящих средних показана ниже (табл. 9.16).

Таблица 9.16. Сглаживание ряда динамики методом скользящей средней по четырем членам

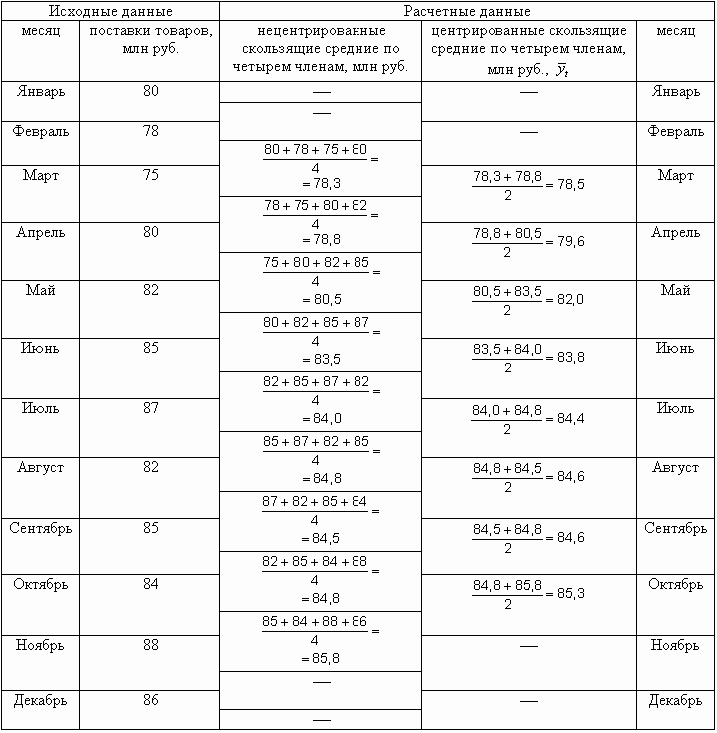9.3.3. Аналитическое сглаживание (выравнивание) рядов динамики

Аналитическое выравнивание динамических рядов — это нахождение определенной модели (уравнения тренда), которая математически описывает тенденцию развития явления во времени. При этом уровни показателя рассматриваются только как функция от времени. В отличие от рассмотренных выше методов, таких, как укрупнение интервалов, скользящих средних, направленных в основном на то, чтобы ответить на вопрос: есть ли тенденция в динамическом ряду или нет, и определить ее направление, аналитическое выравнивание позволяет более точно установить характер развития явления, а главное — описать его математически, уловить все нюансы и направления развития и, что, пожалуй, наиболее интересно, использовать в дальнейшем полученную модель для прогнозирования.

Первым шагом в проведении аналитического выравнивания является выбор вида математической функции, которую предполагается использовать в качестве модели тренда. При этом можно руководствоваться формой кривой, полученной на основе отображения на графике эмпирических данных. Схема построения графика достаточно проста: по оси абсцисс откладываются временные периоды (даты), по оси ординат — значения уровней динамического ряда.

При анализе рядов динамики в качестве линии тренда чаще всего используются следующие функции:

Источник